
- •Определение действительного числа
- •2) Определение абсолютной погрешности
- •3)Определение относительной погрешности
- •4) Определение линейных уравнений с одной переменной
- •5) Определение линейных неравенств с одной переменной
- •6) Системы неравенств с одной переменной и способы их решения
- •7) Квадратные уравнения и способы их решения
- •8) Квадратные неравенства и способы их решения
- •9) Нелинейные неравенства с одной переменной и способы их решения
- •10) Иррациональные уравнения и способы их решения
- •11) Системы двух линейных уравнений с двумя неизвестными и способы их решения
- •12) Определители второго порядка. Формулы Крамера
- •14) Определитель третьего порядка и его вычисления
- •15) Решение систем трёх линейных уравнений с тремя неизвестными с помощью определителей третьего порядка
- •16) Числовая функция и способы её задания
- •17) Свойства функции (область определения и значения)
- •18) Свойства функции (Монотонность функции.)
- •19) Свойства функции (Четность (нечетность), переодичность)
12) Определители второго порядка. Формулы Крамера
Определители второго порядка. Мы видели, что формулы для решения системы двух линейных уравнений с двумя неизвестными имеют вид:
x = ( ce – bf ) / ( ae – bd )
(3)
y = ( af – cd ) / ( ae – bd ) .
Эти формулы легко запоминаются, если ввести для их числителей и знаменателей следующий символ:
 ,
который будет обозначать выражение:
ps – qr .
,
который будет обозначать выражение:
ps – qr .
Это выражение получается перекрёстным умножением чисел p, q, r, s :

и последующим вычитанием одного произведения из другого: ps – qr. Знак « + » берётся для произведения чисел, лежащих на диагонали, идущей из левого верхнего числа к правому нижнему; знак « – » - для другой диагонали, идущей из правого верхнего числа к левому нижнему. Например,
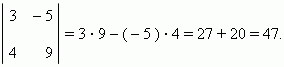
Выражение называется определителем второго порядка.
13) Решение систем 2-х линейных уравнений с двумя неизвестными по формулам Крамера
Правило Крамера. Используя определители, можно переписать формулы (3):
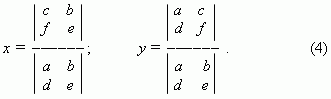
Формулы (4) называются правилом Крамера для системы двух линейных уравнений с двумя неизвестными.
Исследование решений системы двух линейных уравнений с двумя неизвестными, показывает, что в зависимости от коэффициентов уравнений возможны три различных случая:
1) коэффициенты при неизвестных не пропорциональны: a : d ≠ b : e ,
в этом случае система линейных уравнений имеет единственное решение, получаемое по формулам (4);
2) все коэффициенты уравнений пропорциональны: a : d = b : e = c : f ,
в этом случае система линейных уравнений имеет бесконечное множество решений, так как здесь мы имеем фактически одно уравнение вместо двух.
3) коэффициенты при неизвестных пропорциональны, но не пропорциональны свободным членам: a: d = b: e ≠ c: f,
в этом случае система линейных уравнений не имеет решений, так как мы имеем противоречивые уравнения.
14) Определитель третьего порядка и его вычисления
Рассмотрим систему трех линейных уравнений с тремя неизвестными.
a![]() 1x
+ b1y
+ c1z
= d1
1x
+ b1y
+ c1z
= d1
a2x + b2y + c2z = d2 (1)
a3x + b3y + c3z = d3
и покажем, как решение этой системы приводит к определителю третьего порядка.
Умножим обе части первого уравнения системы (1) на l1, второго l2, на третьего на l3, и сложим полученные уравнения:
(a1l1 + a2l2 + a3l3)x +(b1l1 + b2l2 + b3l3)y + (c1l1 + c2l2 + c3l3)z = d1l1 + d2l2 + d3l3 (2)
Выберем l1, l2, l3 так, чтобы коэффициенты при y и z в уравнении (2) равнялись нулю:
b1l1 + b2l2 + b3l3 = 0
c1l1 + c2l2 + c3l3 = 0
или
b1l1 + b2l2 = - b3l3
c1l1 + c2l2 = - c3l3
(3)
Решив систему (3) c помощью алгоритма предыдущего параграфа, найдем l1, l2:
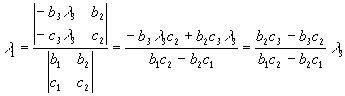
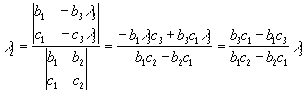
Здесь предполагается, что определитель
![]() не равен нулю.
не равен нулю.
Найденные значения l1,l2 подставим в уравнение (2), тогда получим(a1(b2c3 - b3c2) + a2(b3c1 - b1c3) + a3(b1c2 - b2c1))x = d1(b2c3 - b3c2) + d2(b3c1 - b1c3) + d3(b1c2 - b2c1)
Отсюда следует, что
![]()
если a1b2c3 + a2b3c1 + a3b1c2 - a1b3c2 - a2b1c3 - a3b2c1 № 0
Подобным образом можно найти значения остальных неизвестных.
Определение Определителем третьего порядка, составленным из таблицы
a1 b1 c1 (4)
a2 b2 c2
a3 b3 c3
девяти чисел, называется число
(5)
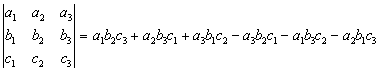
.
Числа, составляющие таблицу (4), называются элементами определителя третьего порядка.
Диагональ сверху вниз направо в этой таблице называется главной диагональю, а диагональ сверху вниз налево - побочной.
Определитель третьего порязка, составленный из таблицы девяти чисел, представляет собой алгебраическую сумму шести произведений; три произведения берутся со знаком + и три произведения - со знаком -.
Со знаком + берется произведение элементов, стоящих на главной диагонали, а также произведения элементов, стоящих на параллели к главной диагонали, с добавлением третьего множителя их противоположного угла таблицы.
Со знаком - берется произведение элементов, стоящих на побочной диагонали, а также произведения элементов, стоящих на параллели к побочной диагонали, с добавлением третьего множителя из противоположного угла таблицы.
