Невероятностные выборки

Отбор в такой выборке осуществляется не по принципам случайности, а по субъективным критериям – доступности, типичности, равного представительства и т.д.

1. Квотная выборка – выборка строится как модель, которая воспроизводит структуру генеральной совокупности в виде квот (пропорций) изучаемых признаков. Число элементов выборки с различным сочетанием изучаемых признаков определяется с таким расчётом, чтобы оно соответствовало их доле (пропорции) в генеральной совокупности. Так, например, если генеральная совокупность у нас представлена 5000 человек, из них 2000 женщин и 3000 мужчин, тогда в квотной выборке у нас будут 20 женщин и 30 мужчин, либо 200 женщин и 300 мужчин. Квотированные выборки чаще всего основываются на демографических критериях: пол, возраст, регион, доход, образование и прочих. Минусы: обычно такие выборки нерепрезентативны, т.к. нельзя учесть сразу несколько социальных параметров. Плюсы: легкодоступный материал.

2. Метод снежного кома. Выборка строится следующим образом. У каждого респондента, начиная с первого, просятся контакты его друзей, коллег, знакомых, которые подходили бы под условия отбора и могли бы принять участие в исследовании. Таким образом, за исключением первого шага, выборка формируется с участием самих объектов исследования. Метод часто применяется, когда необходимо найти и опросить труднодоступные группы респондентов (например, респондентов, имеющих высокий доход, респондентов, принадлежащих к одной профессиональной группе, респондентов, имеющих какие-либо схожие хобби/увлечения и т.д.)

3. Стихийная выборка – выборка так называемого «первого встречного». Часто используется в теле- и радиоопросах. Размер и состав стихийных выборок заранее не известен, и определяется только одним параметром – активностью респондентов. Минусы: невозможно установить какую генеральную совокупность представляют опрошенные, и как следствие – невозможность определить репрезентативность.

4. Маршрутный опрос – часто используется, если единицей изучения является семья. На карте населённого пункта, в котором будет производиться опрос, нумеруются все улицы. С помощью таблицы (генератора) случайных чисел отбираются большие числа. Каждое большое число рассматривается как состоящее из 3-х компонентов: номер улицы (2-3 первых числа), номер дома, номер квартиры. Например, число 14832: 14 – это номер улицы на карте, 8 – номер дома, 32 – номер квартиры.

Районированная выборка с отбором типичных объектов. Если после районирования из каждой группы отбирается типичный объект, т.е. объект, который по большинству изучаемых в исследовании характеристик приближается к средним показателям, такая выборка называется районированной с отбором типичных объектов

27.статистическое распределение(вариационный ряд) Гистограмма. Полигон.

Тогда

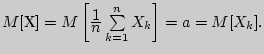
Это обстоятельство приводит к мысли построить статистические характеристики:

Вариационный и статистический ряд

В математической статистике исследуются утверждения, которые могут быть сделаны на основе измерения некоторой величины, на простейшем примере поясним постановку (одной из многих) задач математической статистики.

Пусть требуется измерить некоторую величину . Результаты измерений

Вариационным (статистическим) рядом называется таблица, первая строка которой содержит в порядке возрастания элементы ', а вторая - их частоты (относительные частоты .

Полигоном частот (относительных частот) выборки называется ломаная с вершинами в точках (, ( (, ). естественно рассматривать как значения случайных величин , полученных в данном эксперименте. Если измерительный инструмент не имеет систематической ошибки, то можно положить . Следовательно, возникает задача оценить параметр . Для решения задачи рассмотрим случайную величину

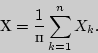
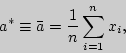
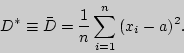Первая представляет среднее арифметическое наблюденных значений случайной величины и статистическую дисперсию - во втором случае. В соответствии с законом больших чисел эти среднеарифметические сходятся по вероятности соответственно к математическому ожиданию величины и к дисперсии

При ограниченности наблюдений эксперимента заменой и на и совершаем погрешность, а при небольшом числе наблюдений величины , являются случайными величинами. Возникает задача об оценке неизвестных параметров , случайной величины на основе экспериментальных данных, т.е. задача - найти подходящие значения этих параметров.

Множество результатов измерений величины называется выборкой объема . Для того, чтобы иметь возможность воспользоваться аппаратом теории вероятностей, целесообразно наблюдаемую величину рассматривать как случайную величину, функцию распределения которой

следует определить.

Полученный статистический материал , , ... наблюдений представляет собой первичные данные о величине, подлежащей статистической обработке. Обычно такие статистические данные оформляются в виде таблицы, графика, гистограммы и т.д.

Если выборка объема содержит различных элементов , причем встречается раз, то число называется частотой элемента , а отношение называется относительной частотой элемента . Очевидно, что

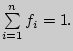
Функция , где - объем выборки, а - число значений в выборке, меньших , называется эмпирической функцией распределения. Функция служит оценкой неизвестной функции распределения , т.е. .

Пусть теперь - непрерывная случайная величина с неизвестной плотностью вероятности . Для оценки по выборке разобьем область значений на интервалы длины . Обозначим через середины интервалов, а через число элементов выборки, попавших в указанный интервал. Тогда - оценка плотности вероятности в точке . В прямоугольной системе координат построим прямоугольники с основаниями и высотами , т.е. площади прямоугольника, равной относительной частоте данного разряда. Полученная таким образом фигура называется гистограммой выборки.

Вариационный ряд — упорядоченная по величине последовательность выборочных значений наблюдаемой случайной величины

равные между собой элементы выборки нумеруются в произвольном порядке; элементы вариационного ряда называются порядковыми (ранговыми) статистиками; число λ_m = m / n называется рангом порядковой статистики

Вариационный ряд используется для построения эмпирической функции распределения. Если элементы вариационного ряда независимы и имеют общую плотность распределения f, то совместная плотность распределения элементов вариационного ряда имеет вид

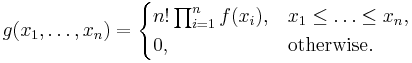
Вариационный ряд. Кроме относительных величин (коэффициентов), характеризующих частоту (интенсивность), либо состав изучаемого явления, статистические совокупности с их количественной стороны могут быть охарактеризованы при помощи средних величин. При изучении физического развития населения , закономерностей течения различных процессов в здоровом и больном организме, для оценки эффективности лекарственных препаратов и решения целого ряда других задач используются средние величины.

Средние величины получаются из рядов распределения (вариационных рядов). В таком ряду количественно изменяющийся признак носит название варьирующего, а отдельные его количественные выражения называются вариантами. Числа, показывающие, как часто встречается та или иная варианта в составе данного ряда, носят название частот. Ряд, в котором сопоставлены варианты и соответствующие этим вариантам частоты и который, следовательно, показывает распределение изучаемой совокупности по величине какого-либо варьирующего признака, носит название вариационного ряда (распределение призывников по росту, новорожденных по весу и т.п.).