- •Раздел 1. Группировка статистических данных
- •Раздел 2. Ряды распределения
- •Раздел 3. Дисперсия. Виды дисперсий. Закон сложения дисперсий
- •Раздел 4. Выборочное наблюдение
- •Раздел 5. Корреляционная связь и её статистическое изучение
- •Раздел 6. Индексы
- •Раздел 7. Ряды динамики
- •Раздел 1. Группировка статистических данных.
- •Зависимость между размером предприятия по стоимости опф и выпуском товаров и услуг
- •Раздел 2. Ряды распределения
- •Ряд, перестроенный в порядке возрастания значения варьирующего признака
- •Расчёт средней арифметической и показателей вариации
- •Раздел 3. Дисперсия. Виды дисперсий. Закон сложения дисперсий.
- •Вспомогательная таблица для расчета общей дисперсии.
- •1 Группа:
- •2 Группа:
- •3 Группа:
- •4 Группа:
- •5 Группа:
- •Вспомогательная таблица для расчета межгрупповой дисперсии.
- •Раздел 4. Выборочное наблюдение
- •Вспомогательная таблица для расчета дисперсии признака в генеральной совокупности.
- •Раздел 5. Корреляционная связь и её статистическое изучение
- •Корреляционная Таблица.
- •Вспомогательная таблица для расчёта сумм слагаемых в системе уравнений.
- •Вспомогательная таблица для расчета сумм слагаемых в формуле коэффициента корреляции.
- •Раздел 6. Индексы
- •Вспомогательная таблица для расчета индексов.
- •Вспомогательная таблица 1.
- •Вспомогательная таблица 2.
- •Раздел 7. Ряды динамики
- •Вспомогательная таблица для расчета показателей рядов динамики.
- •Показатели ряда динамики
Расчёт средней арифметической и показателей вариации
|
Интервалы по xi |
|
|
|
|
|
|
|
|
|
502-823* |
3 |
662,5 |
1987,5 |
3 |
909,5 |
2728,5 |
827190,25 |
2481570,75 |
|
823-1144 |
4 |
983,5 |
3934 |
7 |
588,5 |
2354 |
346332,25 |
1385329 |
|
1144-1465 |
5 |
1304,5 |
6522,5 |
12 |
267,5 |
1337,5 |
71556,25 |
357781,25 |
|
1465-1786 |
7 |
1625,5 |
11378,5 |
19 |
53,5 |
374,5 |
2862,25 |
20035,75 |
|
1786-2107 |
5 |
1946,5 |
9732,5 |
24 |
374,5 |
1872,5 |
140250,25 |
701251,25 |
|
2107-2428 |
6 |
2267,5 |
13605 |
30 |
695,5 |
4173 |
483720,25 |
2902321,5 |
|
Итого: |
30 |
- |
47160 |
- |
- |
12840 |
- |
7848289,5 |
*- верхняя граница включительно.
Средняя арифметическая для интервального ряда рассчитывается по формуле:
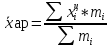
где
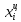 -
центр i-го интервала;
-
центр i-го интервала;
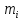 -
частота в i-ом интервале.
-
частота в i-ом интервале.
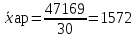
Мода и медиана.
Медиана – это значение признака, приходящееся на середину упорядоченного вариационного ряда.
Медианным является первый интервал, для которого ∑mi превышает половину от общего числа наблюдений (30/2=15). Таким образом, интервал 1465-1786 – медианный, т.к. ∑mi = 3+4+5+7=19.
Для дискретного ряда:
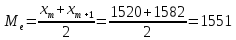
Для интервального ряда:
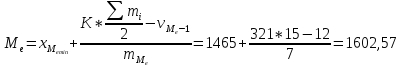
Мода – значение признака, наиболее часто повторяющееся в данном вариационном ряду.
Модальный интервал определяется по наибольшей частоте. Таким образом, интервал – 1465-1786 – модальный.
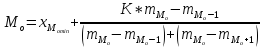
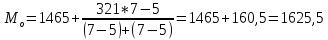
Сравнение моды, медианы и средней позволяет судить о характере распределения признака в совокупности. В данном случае представлена правосторонняя асимметрия:
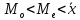 ;
;
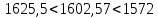 .
.
Показатели вариации.
Показатели вариации позволяют измерить колеблемость значений признака у отдельных единиц совокупности относительно средней, как постоянной величины для данной совокупности.
Для анализа степени вариации рассчитывают следующие абсолютные показатели: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение. Для сравнения вариаций признака в разных совокупностях или вариаций разных признаков в одной совокупности служат относительные показатели - коэффициенты вариации.
Размах вариации:
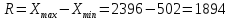
Среднее линейное отклонение:

Среднее квадратическое отклонение:
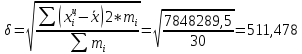
Коэффициенты вариации:
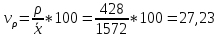

Если
коэффициент вариации
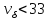 , то совокупность по данному показателю
однородна.
, то совокупность по данному показателю
однородна.
Графические методы изображения вариационных рядов.
1. Гистограмма «Распределение предприятий по выпуску товаров и услуг в марте» (Рис. 1)
2. Полигон «Распределение предприятий по выпуску товаров и услуг в марте» (Рис. 2)
3. Кумулята «Распределение предприятий по выпуску товаров и услуг в марте» (Рис. 3)
4. Огива «распределение предприятий по выпуску товаров и услуг в марте» (Рис. 4)
Вывод:
По
величине коэффициента вариации можно
судить о степени вариации признаков
совокупностей. Чем больше его величина,
тем больше разброс значений признака
вокруг средней, тем менее однородна
совокупность по своему составу и тем
менее представительна средняя. Таким
образом, коэффициент вариации – критерий
типичности средней. В данном случае
коэффициент вариации
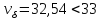 ,
следовательно, средняя типична и вариация
умеренна.
,
следовательно, средняя типична и вариация
умеренна.
Сравнение моды, медианы и средней позволяет судить о характере распределения признака в совокупности. В данном случае распределение асимметрично, т.к. эти характеристики не равны между собой.

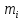
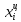
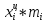
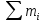
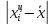
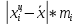
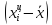 2
2