
- •Критерии сходимости Вейерштрасса монотонной последовательности.
- •Теорема о роли бесконечно малой в теории пределов (об эквивалентности утверждений: и , где -бесконечно малая при
- •Первый замечательный предел.
- •Необходимый признак дифференцируемости ф-ии в точке
- •Теорема Ферма
- •Теорема Роля
- •Теорема Лагранжа.
- •Теорема Коши
- •Теорема о дифференцируемости параметрически заданной функции.
- •Правило Лопиталя для неопределённости вида 0/0
- •Аналитические признаки строгой монотонности (достаточные условия строгой монотонности)
- •Первый достаточный признак локального экстремума.
- •Достаточное условие выпуклости и вогнутости графика функции.
- •Критерий существования наклонной асимптоты.
- •21 Теорема об инвариантности формы первого дифференциала
- •22 Теорема о дифференцируемости сложной ф-ии(1 композиция)
- •23 Понятие градиента. Свойства градиента
- •24 Теорема о необходимом условии существования экстремума функции двух переменных
- •25 Теорема необходимый признак дифференцируемости фнп
- •27 Теорема о непрерывности дифференцируемой фнп в точке
- •Теорема Производная обратной функции
- •Оглавление
25 Теорема необходимый признак дифференцируемости фнп
Если f (x)
дифференцируема в точке х,
то у нее в этой точке существуют все
частные производные и
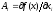 .
.
Доказательство. Дадим приращение хi только одной переменной хi , а остальные переменные оставим без изменения. Тогда
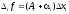 ,
,
где
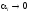 при хi0.
Деля на хi
при хi0.
Деля на хi
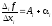
и
устремляя
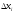 к нулю, получим
к нулю, получим
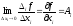 ,
,
что и требовалось доказать.
27 Теорема о непрерывности дифференцируемой фнп в точке
Если
функция u=(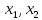 …
…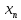 )
дифференцируема в точке
)
дифференцируема в точке
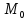 то она непрерывна в этой точке
то она непрерывна в этой точке
Доказательство:
Пусть
u=(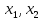 …
…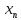 )
– дифференцируема в точке
)
– дифференцируема в точке
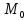 тогда её приращение
тогда её приращение
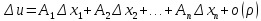 где
где
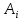 ,
,
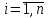 - числа,
- числа,
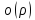 -б.м.
более высокого порядка чем
-б.м.
более высокого порядка чем
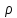
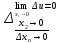 -
определение непрерывности функции
-
определение непрерывности функции
Теорема Производная обратной функции
Пусть
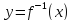 обратная функция к функции
обратная функция к функции
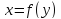 ,
имеющей производную в точку
,
имеющей производную в точку
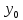 ,
причем
,
причем
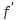 (
(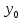 )≠0.
Тогда обратная функция
)≠0.
Тогда обратная функция
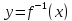 имеет производную
в точке
имеет производную
в точке
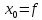 (
(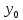 ),
причем
),
причем
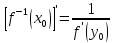 или
или
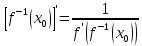
Доказательство
Пусть
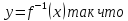
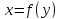 .
Если аргументу
.
Если аргументу
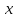 дать приращение
дать приращение
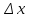 ,то
величина
,то
величина
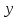 получит приращение
получит приращение
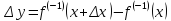 .
Поэтому
.
Поэтому
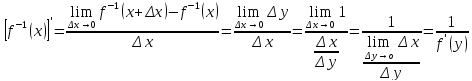
Слева
стоит функция от х, а справа получилась
функция от у. Чтобы устранить это
несоответствие надо в правой части
заменить у на
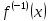 .
Получим
.
Получим
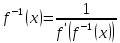
Оглавление
Критерии сходимости Вейерштрасса монотонной последовательности. 1
Теорема о роли бесконечно малой в теории пределов (об эквивалентности утверждений: и , где -бесконечно малая при 1
Первый замечательный предел. 3
Теорема о произведении двух сходящихся последовательностей 4
Теорема об ограниченности сходящейся последовательности 5
Критерий сходимости последовательности Коши 5
Теорема о непрерывности и дифференцируемости функции одного аргумента в данной точке 6
Теорема о производной сложной функции. 7
Теорема о дифференцируемости произведения двух функций. Теорема о производной произведения двух функций 8
Необходимый признак дифференцируемости ф-ии в точке 9
Теорема Ферма 10
Теорема Роля 11
Теорема Лагранжа. 11
Теорема Коши 13
Теорема о дифференцируемости параметрически заданной функции. 13
Правило Лопиталя для неопределённости вида 0/0 15
Аналитические признаки строгой монотонности (достаточные условия строгой монотонности) 17
Первый достаточный признак локального экстремума. 17
Достаточное условие выпуклости и вогнутости графика функции. 18
Критерий существования наклонной асимптоты. 18
21 Теорема об инвариантности формы первого дифференциала 19
22 Теорема о дифференцируемости сложной ф-ии(1 композиция) 19
23 Понятие градиента. Свойства градиента 21
24 Теорема о необходимом условии существования экстремума функции двух переменных 22
25 Теорема необходимый признак дифференцируемости ФНП 23
27 Теорема о непрерывности дифференцируемой ФНП в точке 23
Теорема Производная обратной функции 23
