
- •Критерии сходимости Вейерштрасса монотонной последовательности.
- •Теорема о роли бесконечно малой в теории пределов (об эквивалентности утверждений: и , где -бесконечно малая при
- •Первый замечательный предел.
- •Необходимый признак дифференцируемости ф-ии в точке
- •Теорема Ферма
- •Теорема Роля
- •Теорема Лагранжа.
- •Теорема Коши
- •Теорема о дифференцируемости параметрически заданной функции.
- •Правило Лопиталя для неопределённости вида 0/0
- •Аналитические признаки строгой монотонности (достаточные условия строгой монотонности)
- •Первый достаточный признак локального экстремума.
- •Достаточное условие выпуклости и вогнутости графика функции.
- •Критерий существования наклонной асимптоты.
- •21 Теорема об инвариантности формы первого дифференциала
- •22 Теорема о дифференцируемости сложной ф-ии(1 композиция)
- •23 Понятие градиента. Свойства градиента
- •24 Теорема о необходимом условии существования экстремума функции двух переменных
- •25 Теорема необходимый признак дифференцируемости фнп
- •27 Теорема о непрерывности дифференцируемой фнп в точке
- •Теорема Производная обратной функции
- •Оглавление
Достаточное условие выпуклости и вогнутости графика функции.
Если функция f(x) дважды дифференцируема на интервале (a,b) и ее производная f’’(x)>0 на интервале (a,b) то график функции y = f(x) выпуклый вниз на интервале (a,b).
Если на промежутке a<x<b вторая производная f’’(x) положительна (отрицательна), за исключением отдельных точек, в которых она равна 0, то кривая y = f(x) в этом промежутке вогнута вверх(вниз).
Действительно, если в промежутке a<x<b вторая производная f’’(x), например, положительна , за исключением отдельных точек, в которых она равна 0 , то первая производная f’(x) – возрастающая, а кривая y=f(x), согласно предыдущему, является вогнутой вверх.
Если f’’(x) = 0 не в отдельных точках, а в некотором промежуткеf’(x) – постоянная функция, а f(x) – линейная функция, график ее – прямая линия , и говорить о вогнутости не имеет смысла.
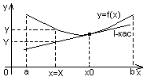
Критерий существования наклонной асимптоты.
Для
того чтобы прямая y
= kx
+ b
была наклонной асимптотой необходимо
и достаточно, чтобы существовали пределы
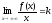 ;
;
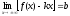
Доказательство:
Точка
Мо(хо,уо) и прямая L:
Аx
+By
+ Cz
= 0 ,То расстояние d(Mo,L)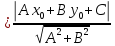
Пусть
y=kx+b
асимптота => d(M,L)
0 => kx
– f(x)
+b
0 , тогда f(x)-kx
b
( при х стремящемуся к плюс бесконечности)
существует предел: lim
(f(x)
– kx)
=b,
(при х стремящемуся к 0 ) . (
+ здесь нада начертить график)


21 Теорема об инвариантности формы первого дифференциала
Если
функция z
= f(x,
y)
удовлетворяет условиям, что функции
x
= x(u,
v)
и y=
y(u,
v)
дифференцируемы в точке (u0,
v0)
и, следовательно, имеют в этой точке
частные производные x¢u
, x¢v
, y¢u
, y¢v
, а функция z
= f(x,
y)
дифференцируема в точке (x0,y0),
где x0
= x(u0, v0),
y0 = y(u0, v0).
Тогда в точке (u0, v0)
существуют и частные производные z¢u
, z¢v
сложной функции z
= f(x(u,
v),
y(u,
v))
и
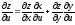
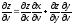 ,
то
,
то
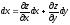
Доказательство:
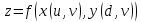 найдем
найдем
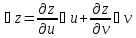 = (
= (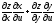 )
)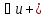
(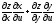 )
)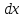 =
=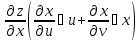 +
+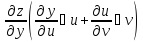 =
=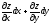 чтд
чтд
22 Теорема о дифференцируемости сложной ф-ии(1 композиция)
Если функции x = x(t) и y = y(t) дифференцируемы в точке t0Î(a, b), а функция z = f(x, y) дифференцируема в точке (x0,y0)ÎD, где x0=x(t0), y0= y(t0), то сложная функция z = f(x(t),y(t)) дифференцируема в точке t0 и в этой точке
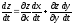
Доказательство:
т.к. z
= f(x,
y)
дифференцируема в
 (x0,y0)
то
(x0,y0)
то
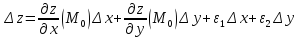 где
где
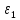 и
и
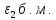 при
при
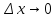
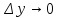 .
Выберем Δx
и Δy
специальным образом зависящие от Δt
.
Выберем Δx
и Δy
специальным образом зависящие от Δt
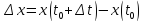 и
и
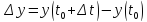
в
силу непрерывности функции x(t)
и y(t)
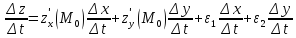 По условию :
По условию :
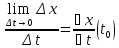
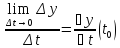 Функции
Функции
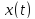 и
и
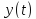 дифференцируемы в точке
дифференцируемы в точке
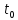
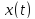 и
и
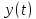 непрерывные
непрерывные
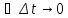 то
то
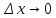
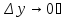
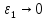
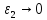 тогда
тогда
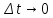 .
При
.
При
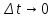 получаем
получаем
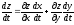
23 Понятие градиента. Свойства градиента
Градиентом
скалярного поля u
=
u(x,
y, z)
в точке M0
называется вектор
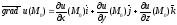 .
.
Свойства:
1.
Градиент в данной точке M0
связан с производной по направлению
формулой
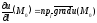 .
.
Доказательство:
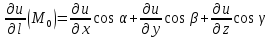 =
=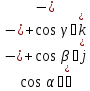 =
=
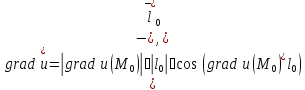 =
=
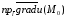
2.
Градиент в данной точке M0
указывает направление наискорейшего
изменения поля в этой точке, а
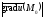 есть наибольшая скорость изменения
поля в точке M0
если направление
есть наибольшая скорость изменения
поля в точке M0
если направление
 совпадает с
совпадает с
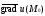 (иначе наименьшее значение).
(иначе наименьшее значение).
Доказательство:
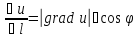 ;
;
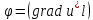 ;
max
;
max
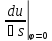 =
=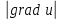
3.Производная по направлению вектора, касательного к поверхности уровня равна нулю.
Доказательство:
U(x,y,z)=C
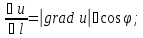
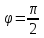 =>
=>
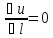
24 Теорема о необходимом условии существования экстремума функции двух переменных
Функция z=f(x,y) имеет max в точке М0(х0,у0), если f(x0,y0)>f(x,y) для любого(х,у), достаточно близких к (.)(х0,у0) и отличных от нее.
Функция Z=f(x,y) имеет min в точке М0(х0,у0), если F(x0,y0)<f(x,y) выполняется для любых точек (х,у), достаточно близких к точке (х0,у0), но отличных от нее.
Точки максимума и минимума функции называются экстремумами функции z=f(x,y); точки в которой частные производные dz/dx=0 dz/dy=0 или не существуют называются критическими.
Теорема. Если функция z=f(x,y) достигает экстремума при х=х0, у=у0, то каждая частная производная первого порядка от Z либо обращается в нуль при этих значениях, либо не существует.
Доказательство:
Пусть у=у0. Тогда f(x,y0) будет функцией одного пременного х. Т.к при х=х0 она имеет экстремум (max или min), то => (dz/dx)x=x0 y=y0 =0 или не существует. Аналогично можно доказать, что (dz/dy)x=x0 y=y0 =0 нулю или не существует. Данное условие не является достаточным условием экстремума в т. Х0, у0.
Достаточное
условие: Пусть дана z=f(x,y)?
введем следующие обозначения: a11=d2z/dx2
a12=d2z/dxdy
a22=d2z/dy2
δ=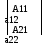
Пусть в некоторой области, содержащей точку М0(х0,у0) функция z=f(x,y) имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того точка М0 является критической точкой функции z=f(x,y), т.е: (df(x0,y0))/dx=0; (df(x0;y0))/dy=0, тогда при х=х0, у=у0:
-
f(x,y) имеет минимум, если a11>0, δ>0 (d2f(x0,y0)>0)
-
f(x,y) имеет максимум, если a11<0, δ>0 (d2f(x0,y0)<0)
-
функция F(x,y) не имеет ни максимума ни минимума, если δ<0 (d2f(x0,y0) меняет знак)
-
если δ=0, то экстремум в точке (х0,у0) может существовать, а может и нет
