Линейная зависимость и независимость свободных векторов:

Векторы , , , называются линейно зависимыми, если существуют числа , , , , не все равные нулю и такие, что линейная комбинация равна нулевому элементу линейного пространства .

Если же равенство возможно только при условии , то векторы , , , называют линейно независимыми.

Критерий линейно зависимости свободных векторов

Векторы ,,, линейно зависимы тогда и только тогда, когда хотя бы один из них линейно выражается через оставшиеся

ДОКАЗАТЕЛЬСТВО

1) Необходимость. Пусть векторы , , , – линейно зависимы. Тогда по определению существуют числа , , , , не все равные нулю и такие, что . Пусть, например, . Тогда

, ⇒ .

2) Достаточность. Пусть один из векторов , , , линейно выражается через оставшиеся. Например, пусть

. ⇒ .

Следовательно, векторы , , , – линейно зависимы

Определение базиса:

Векторы , , , образуют базис в линейном пространстве если выполняются два условия:

1. , , , – линейно независимы;

2. , , , , – линейно зависимы для любого вектора из .

Теорема о базисе

Каждый вектор линейного пространства линейно выражается через любой его базис, причем единственным образом.

ДОКАЗАТЕЛЬСТВО

Пусть , , , – базис линейного пространства и – произвольный вектор из . Тогда, по определению базиса, , , , – линейно независимы и , , , , – линейно зависимы. Следовательно, существуют числа , , , , не все равные нулю и такие, что линейная комбинация ; ≠ 0.

Если , то и среди коэффициенты , , , есть ненулевые. => , , , - линейно зависимы. Это противоречит условию (по условию эти элементы образуют базис и, следовательно, линейно независимы).

Так как , то линейно выражается через , , , :

, ⇒ .

Докажем, что линейно выражается через базис единственным образом. Предположим противное. Пусть

и ,

причем хотя бы для одного . Пусть . Тогда

,

⇒ .

Так как , то . Таким образом, получили, что существует нулевая линейная комбинация векторов , , , , среди коэффициентов которой есть ненулевые. Значит , , , – линейно зависимые. Но они по условию линейно независимы, так как образуют базис.

Следовательно, предположение неверное и вектор разлагается по базису , , , единственным образом.

Скалярное произведение векторов

Скалярным произведением двух ненулевых векторов и называется число, равное произведению их модулей на косинус угла между ними, т.е. число

.

Если или , то скалярное произведение векторов и полагают равным нулю.

Скалярное произведение векторов и обозначают или .

СВОЙСТВА

1. .

2. Скалярное произведение ненулевых векторов и равно произведению длины вектора на проекцию вектора на вектор (длины вектора на проекцию на ).

3..

4. ,.

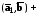
5. .

6. Если a ┴b, то

Критерий ортогональности (перпендикулярности)векторов

Ненулевые векторы и перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю

ДОКАЗАТЕЛЬСТВО

Пусть векторы и перпендикулярны. Тогда

и .

Обратно, пусть и , . Тогда

и , ,

⇒ и . ∎

Скалярное произведение в декартовой системе координат:

Дано:

={a_x;a_y;a_z};

={b_x;b_y;b_z;}

Вывод формулы:

=1 (j,j)=1 (k,k)=1

(i,j)=0 (j,k)=0 (i,k)=0

=(a_xi+ a_y j+ a_z k)( b_xi+ b_y j+ b_z k)= a _xb _x+a _yb _y+a _zb _z

Определение правой тройки векторов

Тройка векторов , и называется правой, если поворот от вектора к вектору на меньший угол виден из конца вектора против часовой стрелки.

Векторным произведением двух ненулевых векторов и называется вектор , удовлетворяющий следующим условиям:

1) , где – угол между векторами и ;

2) вектор перпендикулярен векторам и ;

3) тройка векторов , и – правая.

Если хотя бы один из векторов или нулевой, то их векторное произведение полагают равным нулевому вектору.

Векторное произведение векторов и обозначают или .

СВОЙСТВА:

1. .

2. .

3. , .

4. Ненулевые векторы и коллинеарные тогда и только тогда, когда их векторное произведение равно нулевому вектору (критерий коллинеарности векторов).

5. Модуль векторного произведения неколлинеарных векторов и равен площади параллелограмма, построенного на этих векторах (геометрический смысл векторного произведения).

6. Если в декартовом прямоугольном базисе векторы и имеют координаты: , ,

то .

Заметим, что , , . Теперь, чтобы получить требуемую формулу, достаточно применить к векторному произведению сначала свойство 3, затем свойство 2, и, наконец, свойства 1 и 4.

7. Если вектор это сила, приложенная к точке , то векторное произведение представляет собой момент силы относительно точки (механический смысл векторного произведения).

Смешанным произведением трех векторов , и называется число, равное скалярному произведению вектора на векторное произведение векторов и , т.е. . Если хотя бы один из векторов , или нулевой, то их смешанное произведение равно нулю.

Смешанное произведение векторов , и обозначают или . СВОЙСТВА СМЕШАННОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ

1. .

2. При перестановке любых двух векторов их смешанное произведение меняет знак.

3. .

,

,

.

4. Ненулевые векторы , , компланарны тогда и только тогда, когда их смешанное произведение равно нулю (критерий компланарности векторов).

Если векторы , и компланарны, то вектор перпендикулярен плоскости, в которой лежат эти векторы. Следовательно, и.

Обратно, пусть . Так как , то это означает, что или векторы или .

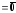Пусть Так как и перпендикулярны вектору , то векторы , и лежат в одной плоскости, т.е. компланарны.

Пусть . Тогда векторы и – коллинеарные и, следовательно, векторы , и лежат в одной плоскости.

6. Если , то векторы , , образуют правую тройку. Если , то тройка векторов , , – левая.

Действительно, пусть . Так как

,

то угол между вектором и – острый. Но тогда поворот от вектора к виден из конца вектора также, как из конца вектора , т.е. против часовой стрелки. Следовательно, тройка векторов , , – правая .

Если 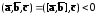, то угол между вектором и – тупой. Но тогда поворот от к из конца вектора и из конца вектора виден в разных направлениях. Значит тройки векторов , , и , , имеют противоположную ориентацию. =>, тройка векторов , , – левая.

7. Модуль смешанного произведения некомпланарных векторов , , равен объему параллелепипеда, построенного на этих векторах (геометрический смысл смешанного произведения).

Объем параллелепипеда, построенного на векторах , , равен .

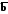Основание параллелепипеда – параллелограмм, построенный на векторах и . Следовательно, его площадь .

Высота параллелепипеда равна , если тройка векторов , , – правая и , если тройка векторов , , – левая.

.

8. Объем пирамиды, построенной на векторах , , равен модуля их смешанного произведения (следствие свойства 7).

(Вычисление смешанного произведения в декартовой системе координат)

9. Если в декартовом прямоугольном базисе векторы , , имеют координаты: , , ,

то .

Действительно, так как и

,

то .

Линейное пространство: Пусть – некоторое множество, элементы которого можно складывать и умножать на действительные (комплексные) числа. Договоримся элементы из обозначать малыми латинскими буквами, а числа – малыми греческими буквами. Тогда Множество называется линейным пространством над ℝ(ℂ) если для любых элементов и для любых чисел ℝ(ℂ) выполняются условия:

1. (коммутативность сложения элементов из );

2. (ассоциативность сложения элементов из );

3. Во множестве существует такой элемент , что . Этот элемент называют нулевым элементом множества ;

4. Для любого элемента существует элемент такой, что . Элемент называют противоположным к ;

5. (ассоциативность относительно умножения чисел);

6. (дистрибутивность умножения на элемент из относительно сложения чисел);

7. (дистрибутивность умножения на число относительно сложения элементов из );

8. .

ПРИМЕРЫ линейных пространств.

1) Пусть ℝ – множество матриц размера с элементами из ℝ. Для этого множества все условия определения выполняются . Следовательно, множество ℝ является линейным пространством над ℝ.

2) Пусть () – множество свободных векторов пространства (плоскости). Для этого множества тоже выполняются все условия определения Следовательно, множество () является линейным пространством над ℝ.

Определение подпространства, критерии

Пусть – линейное пространство над ℝ(ℂ), – непустое подмножество в .

Тогда говорят, что является подпространством линейного пространства (или линейным подпространством), если оно само образует линейное пространство относительно операций, определенных на .

Справедлива следующая теорема.

ТЕОРЕМА (критерий подпространства). Пусть – линейное пространство над ℝ(ℂ), – непустое подмножество в . является подпространством линейного пространства тогда и только тогда, когда для любых элементов и любого ℝ выполняются условия: 1) ; 2) .

Определение линейной зависимости и независимости

Пусть – линейное пространство над ℝ(ℂ), , , , .

Тогда говорят, что векторы , , , линейно зависимы, если существуют числа , , , , не все равные нулю и такие, что линейная комбинация равна нулевому элементу линейного пространства .

Если же равенство возможно только при условии , то векторы , , , называют линейно независимыми