Критерий существования обратной матрицы

Пусть – квадратная матрица порядка . Матрица имеет обратную тогда и только тогда, когда ее определитель отличен от нуля. Причем обратная матрица может быть найдена по формуле:

,

где – матрица из алгебраических дополнений элементов матрицы , т.е.

.

Матрица называется союзной для матрицы .

ДОКАЗАТЕЛЬСТВО

Необходимость утверждения доказана ранее (см. свойство 3 матриц, имеющих обратную). Требуется доказать только достаточность.

Пусть матрица – невырожденная. Тогда существует матрица . Докажем, что она является обратной к 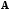. Имеем:

.

Здесь использовали, что (следствие 2.2 теоремы Лапласа), (следствие 2.3 теоремы Лапласа).

Аналогично доказывается, что

.

Следовательно, . ∎

Матричный метод решения системы

Рассмотрим теперь систему линейных уравнений, в которой число уравнений и число неизвестных совпадает и . Тогда:

1) и, следовательно, такая система имеет единственное решение;

2) матрица имеет обратную матрицу .

Запишем систему в матричной форме: .

Умножим обе части равенства на слева. Получим:

, ⇒ , ⇒ ,

⇒ .

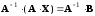Если в системе линейных уравнений и 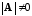, то система имеет единственное решение, которое можно найти по формуле .

Метод Крамера

Если в системе линейных уравнений число уравнений и число неизвестных совпадает и , то система совместна и имеет единственное решение, которое может быть найдено по формулам

(), где , а – определитель, получаемый из определителя заменой его -го столбца на столбец свободных членов.

ДОКАЗАТЕЛЬСТВО

Так как , то матрица имеет обратную и систему можно решить матричным методом, т.е.

,⇒ .

Но выражение 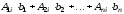представляет собой разложение по -му столбцу определителя 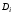. Следовательно,

. ∎

СЛОУ – называется однородной, если все свободные члены равны нулю:

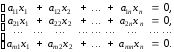
эта система всегда совместна, так как всегда является ее решением. Это решение называют тривиальным. Система имеет не тривиальное решение если и или если (в обоих случаях и, следовательно, система имеет множество решений)

Фундаментальной системой решений (фср), системы одно­родных линейных уравнений называется совокупность решений, которая обладает двумя свойствами:

а) ФСР состоит из (n — R) линейно независимых решений;

б) любое решение системы можно представить в виде линей­ной комбинации фундаментальной системы решений

Определение проекции вектора на ось:

Прямую, на которой выбрано направление, называют осью.

Пусть имеется некоторая ось и вектор . Обозначим через и ортогональные проекции на ось точек и соответственно. Вектор назовем векторной проекцией вектора на ось .

ОПРЕДЕЛЕНИЕ. Проекцией (ортогональной проекцией) вектора на ось называется длина его векторной проекции на эту ось, взятая со знаком плюс, если вектор и ось сонаправлены, и со знаком минус – если вектор и ось противоположно направлены.

Свойства проекицй:

1) Равные векторы имеют равные проекции

2) Проекция суммы векторов на одно и то же направление равна сумме проекций каждого вектора на это направление

3) При умножении вектора на число его проекция умножается на это число

Направляющие косинусы в декартовой системе координат

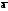Обозначим через , и углы, которые вектор образует с координатными осями , и соответственно. , , называются направляющими косинусами вектора . Найдем направляющие косинусы вектора через его координаты:

Находим:

, .

Следовательно,

, , .

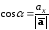свойство напр. косинусов .

ТЕОРЕМА О сведении линейных операций над векторами к таким же операциям над их одноименными координатами.

1) Если вектор имеет в базисе , , , координаты , вектор имеет в том же базисе координаты , то вектор будет иметь в базисе , , , координаты .

2) Если вектор имеет в базисе , , , координаты , то для любого числа ℝ вектор будет иметь в том же базисе координаты .

ДОКАЗАТЕЛЬСТВО

По условию , .

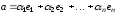Тогда

и .