
- •1. Предмет теории вероятностей
- •2. Из теории возникновения и развития теории вероятностей
- •3. События и их вероятности. Статистическое определение вероятности
- •4. Пространство элементарных событий
- •5. Действия над событиями
- •6. Классическое определение вероятности
- •7. Формула сложения вероятностей для несовместных событий
- •8. Формула сложения вероятностей для общего случая
- •9. Формулы умножения вероятностей
- •10. Формула полной вероятности
- •11. Формула вероятностей гипотез (формула Байеса)
- •12. Геометрическое определение вероятности.
- •13. Метод Монте-Карло
12. Геометрическое определение вероятности.
Классическое определение вероятности предполагает, что число элементарных исходов конечно. На практике встречаются опыты, для которых множество таких исходов бесконечно.
В этом случае классическое определение вероятности неприменимо и вводят геометрические вероятности – вероятности попадания точки в область.
Н а
плоскости задана квадрируемая область
имеющая площадь. Обозначим эту область
–
а
плоскости задана квадрируемая область
имеющая площадь. Обозначим эту область
–
![]() ,
её площадь
,
её площадь
![]() .
В области
.
В области
![]() содержится
область
содержится
область
![]() площади
площади
![]() .
.
G

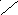



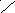
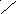
g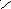

В область
![]() на удачу бросается точка. Будем считать,
что брошенная точка может попасть в
некоторую часть области
на удачу бросается точка. Будем считать,
что брошенная точка может попасть в
некоторую часть области
![]() с вероятностью, пропорциональной площади
этой части и не зависящей от её формы и
расположения.
с вероятностью, пропорциональной площади
этой части и не зависящей от её формы и
расположения.
Пусть
![]() – попадание брошенной точки в область
– попадание брошенной точки в область
![]() ,
тогда геометрическая вероятность этого
события определяется формулой:
,
тогда геометрическая вероятность этого
события определяется формулой:
![]() .
.
Аналогично вводится
понятие геометрической вероятности
при бросании точки в пространственную
область
![]() объёма
объёма
![]() ,
содержащую область
,
содержащую область
![]() объёма
объёма
![]() :
:
![]() .
.
В общем случае
понятия геометрической вероятности
вводится следующим образом. Обозначим
меру области
![]() через
через
![]() ,
а меру области
,
а меру области
![]() .
.
Пусть
![]() – событие попадание брошенной точки в
область
– событие попадание брошенной точки в
область
![]() ,
которая содержится в области
,
которая содержится в области
![]() .
Вероятность попадания в область
.
Вероятность попадания в область
![]() точки, брошенной в область
точки, брошенной в область
![]() ,
определяется формулой
,
определяется формулой
![]() .
.
Пример. Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов независимо и равновозможно в течение данных суток. Определить вероятность того, что одному из пароходов придется ожидать освобождение причала, если время стояния первого парохода равно одному часу, а второго – двум часам.
Решение.
Обозначим через
![]() и
и
![]() время прибытия значения пароходов.
Возможные значения
время прибытия значения пароходов.
Возможные значения
![]() и
и
![]() :
:
![]()
![]()
Благоприятствующие
значения
![]() :
:
![]() и
и
![]() .
.
Если первый пришёл
в момент
![]() ,
то второй должен придти через 1 час,
т.е.
,
то второй должен придти через 1 час,
т.е.
![]() ,
откуда
,
откуда
![]() .
.
Е сли
второй пришёл в момент
сли
второй пришёл в момент
![]() ,
то первый должен подойти через 2 часа,
т.е.
,
то первый должен подойти через 2 часа,
т.е.
![]() .
.
Эти неравенства определяют область (заштрихованную).
Найдём её площадь:
![]() ;
;
![]()
13. Метод Монте-Карло
Геометрическая интерпретация вероятности события дала толчок к появлению вычислительного метода – метода Монте-Карло, или метода статических испытаний. Суть метода поясним на следующем примере. Нужно вычислить интеграл:
![]() ,
,
положим
![]() .
В этом случае
.
В этом случае
![]() – площадь
криволинейной трапеции.
– площадь
криволинейной трапеции.
Пусть
![]() достаточно сложная функция, первообразная
которой не выражается через элементарные
функции.
достаточно сложная функция, первообразная
которой не выражается через элементарные
функции.
Р ассмотрим
прямоугольник высотой h
и основанием
ассмотрим
прямоугольник высотой h
и основанием
![]() ,
таким, что
,
таким, что
![]() .
.
Пусть мы можем моделировать бросание наудачу точки в этот прямоугольник. Тогда, производя достаточно большое число испытаний, можно найти частоту попадания случайной точки в заштрихованную область. При достаточно большом числе опытов n эта частота будет близка к вероятности р – попадания случайной точки в заштрихованную область.
![]() ,
откуда
,
откуда
![]() ,
,
где т – число попаданий точки в заштрихованную область. Наличие мощных компьютеров делает задачу моделирования испытаний несложной.
Этот прием можно распространить и на многомерные интегралы.
Многие задачи вычислительной математики решаются методом Монте-Карло более эффективно, чем традиционными способами.
