10. Формула полной вероятности
Предположим, что
событие
может произойти вместе с одним из событий
,
образующих полную группу несовместимых
событий. Полная группа – это значит,
что должно появиться хотя бы одно
событие. Эти события называются
гипотезами. Т.к.
полная группа, то
,
т.е. их сумма достоверное событие.
Умножим это
равенство на
:
.
Произведение
события
на событие достоверное есть само событие
Вычислим вероятность
события
.
Согласно теореме об умножении вероятностей:
.
Это и есть формула полной вероятности.
Пример. Имеются три одинаковые урны.
В первой: 2 белых и 1 черный шар;
Во второй: 3 белых и 1 черный шар;
В третьей: 2 белых и 2 черных шара.
Выбирается наудачу одна из урн и из нее вынимается один шар. Найти вероятность того, что он белый.
Решение: Здесь гипотезами является выбор урны
- выбор первой,
- выбор второй,
- выбор третьей.
Ясно, что
.
Если выбрали первую урну, то вероятность
того, что вынутый шар белый равна
.
Если вторую, то
.
Если третью, то
.
,
.
11. Формула вероятностей гипотез (формула Байеса)
Имеется полная
группа несовместимых гипотез
,
вероятности которых до опыта известности
и равны:
.
Эти вероятности называют априорными.
Произведем опыт,
в результате которого появилось некоторое
событие
.
Возникает задача: как следует изменить вероятности гипотез в связи с появлением этого события? Т.е. речь идет о нахождении условных вероятностей.
- их называют
априорные вероятности.
По теореме умножения имеем:
,
откуда
.
По формуле полной вероятности имеем:
,
тогда
.
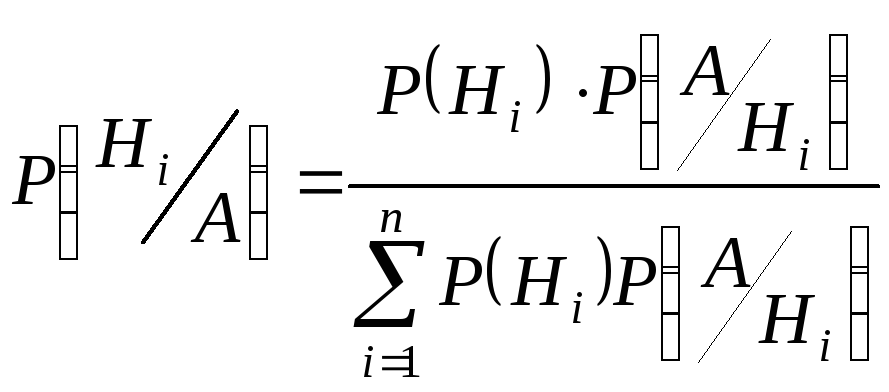
Это и есть формула Байеса или формула вероятностей гипотез.
Формула Байеса
позволяет переоценить вероятность
гипотез после того, как становится
известным результат испытания, в итоге
которого появилось событие
.
Примеры
1) В условиях задачи предыдущего параграфа вычислить вероятности появления белого шара из первой, второй, третьей урн.
Решение:
I. 2 белых, 1 черный
.
II. 3 белых, 1 черный
.
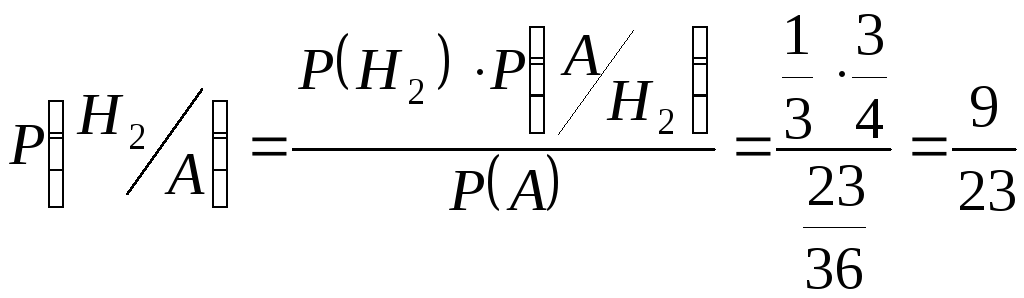III. 2 белых, 2 черных
.
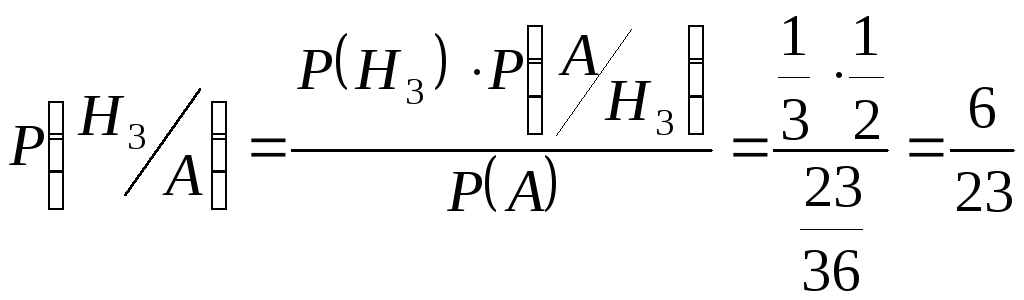2) Из партии в пять деталей наудачу взято одно изделие, оказавшееся бракованным. Количество бракованных изделий равновозможно любое. Какое предположение о количестве бракованных изделий наиболее вероятно?
Решение. До опыта возможны гипотезы:
- в партии 0
бракованных изделий,
- в партии 1
бракованное изделие,
k=0,
1,2,3,4,5
………………………………………….,
- в партии 5
бракованных изделий.
Вероятность этих
гипотез
,
т.к. по условию задачи равновозможно
любое количество бракованных изделий.
Наблюдается событие
– изделие бракованное
,
,
,
……………,
.
Эта вероятность
наибольшая при k=5.
Т.о. наиболее вероятная гипотеза
– все пять изделий бракованные.
3) 60% изделий собирались в первые три недели месяца и 40% в последнюю неделю. Если телевизор собран в последнюю неделю, то вероятность доработать до конца гарантийного срока равна 0,7, если в первые три – до 0,95. Купили телевизор и он вышел из строя до конца гарантийного срока. Найти вероятность того, что он был выпущен в последнюю неделю.
Решение. Гипотезы:
– телевизор выпущен в первые три недели,
– телевизор выпущен
в последнюю неделю.
Априорные вероятности
,
.
Событие
– выход из строя до конца гарантийного
строя.
Вероятность
,
.
.
4) Изделие может
собираться из высококачественных
деталей и из деталей обычного качества.
40 % изделий собирается из высококачественных
деталей. Если изделие собрано из
высококачественных деталей, то его
надежность (вероятность безотказной
работы) за время
равна 0,95. Если из обыкновенных деталей
– равна 0,7. Провели испытание изделия
в течение времени
,
и работало оно безотказно. Найти
вероятность того, что изделие собрано
из высококачественных деталей.
Решение. Возможны две гипотезы:
– собрано из высококачественных деталей,
– собрано из обычных деталей.
Вероятность этих гипотез до опыта:
,
.
В результате опыта
наблюдено событие
– изделие работало безотказно время
.
Условные вероятности этого события при
гипотезах
и
равны:
,
.
Находим вероятность
гипотезы
после опыта:
.
5) Из партии в пять деталей наудачу взято одно изделие, оказавшееся бракованным. Количество бракованных изделий равновозможно любое. Какое предположение о количестве бракованных изделий наиболее вероятно?
Решение. До опыта возможны гипотезы:
– в партии k изделий
бракованных.
.
.
Наблюдается событие
– изделие бракованное.
,
,
,
или в общем
виде: 
.
.
Эта вероятность
наибольшая при
.
Т.е. наиболее вероятная гипотеза
– все изделия – брак.
6) Вероятность
попадания при каждом выстреле для 3х
стрелков равны
,
,
.
При одновременном выстреле всех трех
стрелков имелось два попадания. Определить
вероятность того, что промахнулся третий
стрелок.
Решение. До опыта возможны гипотезы:
– промахнулся 1 стрелок
,
– промахнулся 2стрелок
,
– промахнулся 3стрелок
,
– промахнулись 1 и 2 стрелки,
– промахнулись 1 и 3 стрелки,
– промахнулись 2 и 3 стрелки,
– промахнулись 1, 2 и 3 стрелки,
– никто не промахнулся.
Введем событие
– промах
го
стрелка.
,
,
.
.
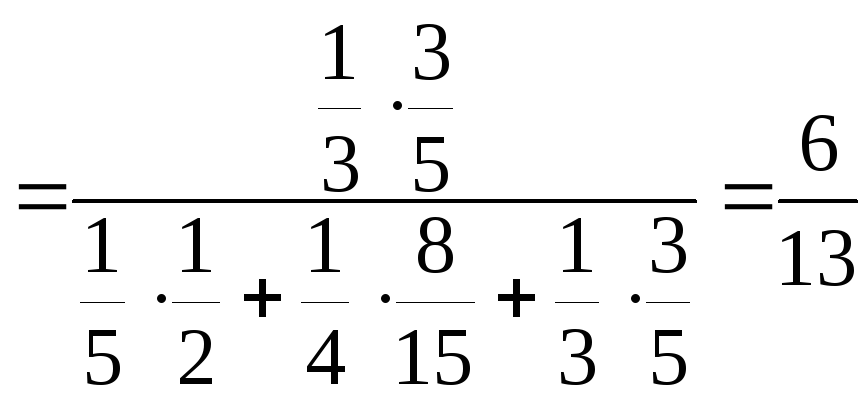