7. Формула сложения вероятностей для несовместных событий

Теорема

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

.

Доказательство.

Рассмотрим схему случаев:

– случаев, благоприятных появлению ,

– случаев, благоприятных появлению ,

– возможных исходов опытов.

, .

Т.к. и несовместны, то нет таких случаев, которые благоприятствовали бы и вместе. Таким образом, событию благоприятствуют случаев.

.

Аналогично докажется событии:

.

Следствие 1.

Если события образуют полную группу несовместных событий, то сумма их вероятностей равна единице:

,

где – достоверное событие. Т.к. – несовместны, то согласно теореме:

.

Следствие 2.

Сумма вероятностей противоположных событий равна единице.

и .

или

.

Примеры

1. Стрелок производит 1 выстрел в мишень, состоящую из центрального круга и двух концентрических колец. Вероятности попадания в круг и кольца соответственно равны: 0,20; 0,15; 0,10.

Определить вероятность промаха.

Решение. – промах, – попадание.

.

,

,

.

2. В лотерее 1000 билетов, из них на один билет подает выигрыш 500р., на 10 – по 100р., на 50 – 20р., на 100 – 5р. Остальные билеты без выигрыша. Купив один билет, найти вероятность выиграть не менее 20р.

Решение.

– выигрыш не менее 20р.,

– выигрыш 20р.,

– выигрыш 100р.,

– выигрыш 500р.

.

.

8. Формула сложения вероятностей для общего случая

Пусть и совместны. Запишем тождество

.

Но тогда и несовместны и к ним применима формула сложения вероятностей несовместных событий:

. (1)

Событие В можно составить так:

– А

– В

– А·В

– В – А·В

События и – несовместны.

. (2)

Из (1) вычтем (2):

,

.

Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.

Вычислим вероятность суммы 3^х совместных событий:

Аналогично выводятся для большего числа событий.

Пример. Бросаются 2 монеты. Рассматриваются 2 события.

А – выпадение герба на 1^ой монете,

В – выпадение герба на 2^ой монете.

Найти вероятность (вероятность появления хотя бы одного герба).

Решение.

События А и В совместны:

.

9. Формулы умножения вероятностей

Введем понятие о независимых и зависимых событиях:

Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.

Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Примеры

1) Бросание 2^х монет.

А

– эти два события независимы

– появление герба на 1^ой,

В– появление цифры на 2^ой.

2) В урне 3 белых и 2 черных шара. Опыт состоит в том, что Иван и Петр вынимают из урны по одному шару.

Рассматриваются события:

А – появление белого шара у Ивана,

В – появление черного шара у Петра.

До того, как что-либо известно о событии В, вероятность события А равна:

.

Если же известно, что событие В произошло (черный шар у Петра), вероятность уже будет равна:

,

из чего следует, что событие А зависит от В.

Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается .

Таким образом, в нашем примере .

Если события независимы, то

,

если же зависимы, то

.

Теорема умножения вероятностей

Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место.

.

Доказательство. Используем схему случаев.

Событию А благоприятствуют т случаев, событию В благоприятствуют k случаев.

А и В не предполагаются несовместными, значит, существуют случаи, благоприятствующие событию А и В одновременно, их число l.

Событию АВ благоприятствуют случаев.

Вычислим вероятности.

,

.

Т.к. известно, что произошло, то из ранее возможных случаев остаются возможными только случаев, из них – благоприятно событию , откуда

,

отсюда

.

Замечание: При применении теоремы умножения безразлично какое из событий считать первым, какое вторым, поэтому:

.

Следствие 1.

Если событие не зависит от события , то и событие не зависит от события .

Доказательство.

,

,

,

,

.

Таким образом, зависимость или независимость всегда взаимны.

В дальнейшем и будем называть просто независимыми событиями, если появление одного из них не изменяет вероятности другого.

Следствие 2.

Вероятность произведения двух независимых событий равна произведению вероятности этих событий.

,

т.к. для независимых событий , то

.

Сформулируем теорему умножения вероятностей для большого числа событий.

Вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие имели место.

.

В случае независимых в совокупности событий будем иметь:

,

т.е. вероятность произведения независимых событий равна произведению вероятностей этих событий.

Примеры

1) В урне 2 белых и 3 черных шара. Из урны вынимают подряд 2 шара. Найти вероятность того, что оба шара белые.

Решение.

– оба шара белые,

– появление белого шара при 1^ом вынимании,

– появление белого шара при 2^ом вынимании.

.

.

2) Прибор состоит из двух дублирующих линий, в каждую из которых включено по 2 блока с вероятностями отказов и .

Найдем вероятность отказа всего прибора в целом.

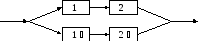
Решение. Пусть – отказ 1^го блока,

– отказ 2^го блока,

– отказ 1 ́ блока,

– отказ 2 ́ блока.

,

.

Величина надежности расценивается так:

,

таким образом, это есть вероятность безотказной работы.

Пусть .

.

Если исключить дублирующую линию, то надежность уменьшится. Действительно, в этом случае:

.