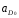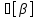- •2.2.Определения скоростей. Определение скоростей линейных точек.
- •2.3. Определение линейных ускорений шарнирных точек
- •3. Синтез зубчатого механизма
- •3.1 Кинематическая схема зубчатой передачи
- •3.2 Общее передаточное отношение зубчатой передачи
- •3.2.4. Коэффициент перекрытия
- •4. Синтез кулачкового механизма
- •4.1. Определение закона движения толкателя
- •5. Приведение сил и масс машинного агрегата
- •5.1. Приведение сил машинного агрегата
- •5.1.2. Приведенный момент сил
- •5.2. Приведение масс машинного агрегата :
- •5.3. Момент инерции маховика :
- •5.5. Выбор приводного электродвигателя
- •6. Силовой расчет главного механизма
- •6.2. Силовой расчет группы Ассура 2 – 3
- •6.3. Структурная группа 4–5
- •6.4. Силовой расчет начального звена
- •Список литературы
1. Структурный анализ главного механизма
1.1. Кинематическая схема главного механизма

Рис.1
По формуле Чебышева определим число степеней подвижности механизма:
W = 3n - 2P5 - P4 = 3 ∙ 5 - 2 ∙ 7 - 0 = 1,
где n = 5- число подвижных звеньев;
P5 = 7(0-1; 1-2; 1-4; 2-3; 3-0; 4-5; 5-0) - число кинематических пар 5-го класса;
P4 = 0 - число кинематических пар 4-го класса.
Вывод. В механизме одно начальное звено.
1.2. Построение структурной схемы механизма
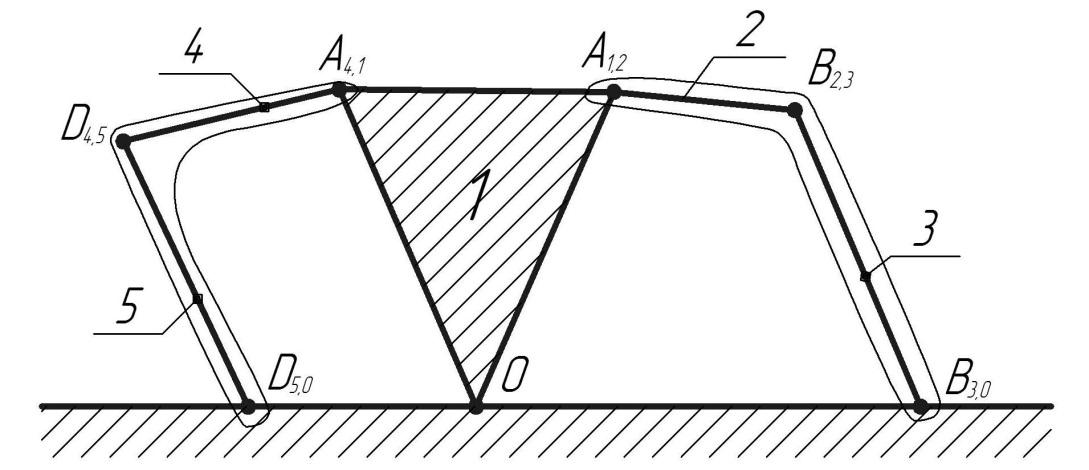
Рис. 2
Выделим структурные группы: группа из звеньев 2 и 3; группа из звеньев 4 и 5,
2-й порядок. 2-й класс по Артоболевскому.
2. Кинематическое исследование дизеля
Для проведения
кинематического анализа на листе 1
построим кинематическую схему механизма
для 8 положений начального звена с
шагом
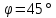 .
.
2.1. Определение масштаба длин
Для построения планов положения механизма необходимо определить масштаб длин по формуле:
где
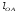 =0,096
[м]
– истинная
длина кривошипа (звено 1);
=0,096
[м]
– истинная
длина кривошипа (звено 1);
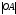 =48
мм – отрезок, изображающий на
кинематической схеме длину кривошипа
(задан произвольно).
=48
мм – отрезок, изображающий на
кинематической схеме длину кривошипа
(задан произвольно).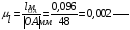
Определяем размеры звеньев на чертеже:
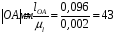
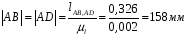
По планам положений механизма строим график перемещений ползуна 3.
2.2.Определения скоростей. Определение скоростей линейных точек.
Используя две теоемы механики запишем векторные уравнения скоростей
по группам Ассура :
Векторные уравнения скоростей
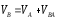
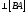 (2.2.1)
(2.2.1)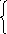

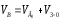
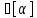
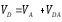
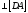 (2.2.2)
(2.2.2)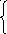

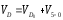
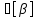
Эти векторные уравнения будем решать графически построением планов скоростей
в масштабе :
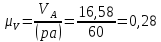
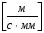
где
 =
=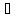 1∙lOA
,
1∙lOA
,
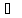 1=
1=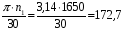 с-1,
с-1,
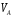 =172,7∙0,096=16,58
=172,7∙0,096=16,58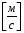 .
.
Результаты кинематического исследования приведем в таблицу 2.1.
Таблица 2.1.
|
№ полож Парам. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Pb |
0 |
51,4 |
60 |
33,4 |
0 |
33,4 |
60 |
51,4 |
|
Vb |
0 |
14,4 |
16,8 |
9,35 |
0 |
9,35 |
16,8 |
14,4 |
|
Pd |
52,3 |
19,95 |
37,3 |
62,6 |
43,7 |
11,1 |
22,26 |
53,3 |
|
Vd |
14,6 |
5,58 |
10,44 |
17,53 |
12,2 |
3,11 |
6,23 |
15 |
|
pS2 |
40 |
53,5 |
60 |
48,5 |
40 |
48,5 |
60 |
53,5 |
|
Vs2 |
11,2 |
14,98 |
16 |
13,58 |
11,2 |
13,58 |
16 |
14,9 |
|
pS4 |
55,7 |
42,2 |
47,66 |
60,38 |
52,8 |
41,15 |
44,33 |
57,4 |
|
Vs4 |
15,6 |
11,82 |
13,3 |
17 |
14,8 |
11,5 |
12,4 |
16,1 |
|
ab |
60 |
43,4 |
0 |
43,4 |
60 |
43,4 |
0 |
43,4 |
|
|
51,5 |
37,3 |
0 |
37,3 |
51,5 |
37,3 |
0 |
37,3 |
|
ad |
29,24 |
58 |
52,5 |
16,2 |
30,8 |
58,1 |
52,5 |
16,2 |
|
|
25,1 |
49,8 |
45,1 |
14 |
26,4 |
50 |
45,1 |
14 |
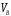 =(pb)
μV
=(pb)
μV
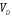 =(pd)
μV
=(pd)
μV
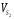 =(pS2)
μV
=(pS2)
μV
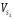 =(pS4)
μV
=(pS4)
μV
Угловые скорости звеньев 2 и 4 определим через соответственные
относительные скорости :

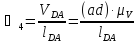
2.3. Определение линейных ускорений шарнирных точек
Запишем векторные уравнения ускорений по группам Ассура :
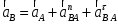 (2.3.1)
(2.3.1)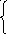

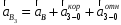 ;
;
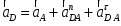 (2.3.2)
(2.3.2)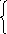

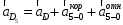
Сведения о векторнах ускорений приведены в таблице 2.2.
Таблица 2.2.
|
Вектор |
Величина |
Направление |
Отрезок на плане ускорений |
||
|
Полож. 4 |
Полож. 8 |
||||
|
|
|
От А к О |
|
||
|
|
4 = 453,56 8 = 453,56 |
От В к А |
|
|
|
|
|
неизвестно |
|
----------------- |
----------------- |
|
|
|
0 |
------------------ |
----------------- |
---------------- |
|
|
|
0 |
------------------ |
------------------ |
---------------- |
|
|
|
неизвестно |
|
------------------ |
---------------- |
|
|
|
4 = 63,9 8 = 63,9 |
От D к А |
|
|
|
|
|
неизвестно |
|
----------------- |
----------------- |
|
|
|
0 |
----------------- |
---------------- |
--------------- |
|
|
|
0 |
----------------- |
---------------- |
---------------- |
|
|
|
неизвестно |
|
----------------- |
---------------- |
|
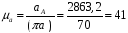
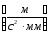 – масштаб плана
ускорения.
– масштаб плана
ускорения.
Из плана ускорений определяем ускорения центра масс шатунов , используя свойство подобия :
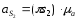 ,
,
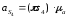
Линейные ускорения
Положение № 4
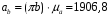
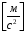
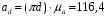
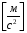
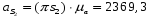
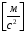
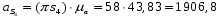
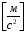
Определение угловых ускорений шатунов :
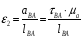 ,
,
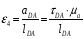
Положение № 4 :
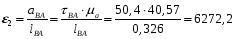
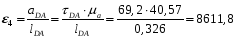

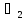
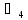
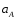
 12∙lOA
=2863,2
12∙lOA
=2863,2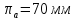
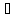 22∙lВА
22∙lВА
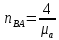
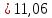
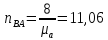
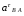
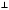
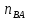
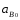
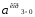

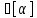
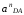
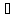 42∙lDА
42∙lDА