
- •1. Линейные пространства
- •Дайте определение линейного пространства. Приведите примеры линейных пространств.
- •Дайте определение линейно зависимой системы векторов. Приведите примеры. Будет ли линейно зависима система, включающая нулевой вектор? Ответ обоснуйте.
- •Дайте определение линейно независимой системы векторов. Приведите примеры. Будет ли линейно независимой лестничная система векторов? Ответ обоснуйте.
- •Дайте определение базиса линейного пространства. Докажите, что координаты вектора в данном базисе определены однозначно.
- •Что называется размерностью линейного пространства ? Может ли система из векторов, где , являться базисом - мерного пространства ? Ответ обоснуйте.
- •Пусть - векторы из . Можно ли составить базис пространства из линейных комбинаций этих векторов? Ответ обоснуйте.
- •Дайте определение подпространства линейного пространства и приведите пример. Как связаны размерности пространства и его подпространства? Ответ обоснуйте.
- •Какие из множеств, образованных всевозможными векторами из такими, что а) , б) , в) , являются подпространствами в , а какие нет? Ответ обоснуйте.
- •2. Системы линейных уравнений
- •Какие системы уравнений называются определенными, неопределенными, несовместными? Приведите примеры. Может ли однородная система линейных уравнений быть несовместимой?
- •Докажите, что однородная система, состоящая из трех уравнений от пяти переменных, имеет бесконечно много решений.
- •Как связаны решения совместной неоднородной системы линейных уравнений и однородной системы ? Приведите пример.
- •Дайте определение фундаментального набора решений однородной системы линейных уравнений. Приведите пример системы и найдите ее фундаментальный набор решений.
- •Найдите фундаментальный набор решений системы:
- •Пусть дан фундаментальный набор решений некоторой однородной системы: , . Укажите другой фундаментальный набор решений этой системы. Ответ обоснуйте.
- •3. Евклидовы пространства
- •Дайте определение ортогонального базиса в . Приведите пример ортогонального базиса в , не содержащего ни одного из векторов стандартного базиса , , . Ответ обоснуйте.
- •4. Матрицы и определители
- •5. Комплексные числа
- •6. Линейные операторы в пространстве
- •Докажите, что собственные векторы квадратной матрицы 3*3, отвечающие различным собственным значениям, линейно независимы.
- •Как связаны собственные векторы и собственные значения квадратных матриц и ? Ответ обоснуйте.
- •Как связаны собственные векторы и собственные значения квадратных матриц и , где - невырожденная матрица? Ответ обоснуйте.
- •Какому алгебраическому уравнению удовлетворяют собственные значения матрицы? Приведите пример.
- •Докажите что подобные матрицы имеют одинаковые характеристические многочлены.
- •Дайте определение числа Фробениуса неотрицательной квадратной матрицы. Найдите число Фробениуса для матрицы : (а) ; (б) . Ответы обоснуйте.
- •Сформулируйте критерий продуктивности матрицы. Приведите пример продуктивной матрицы порядка 3*3
- •7. Квадратичные формы
- •Дайте определение матрицы квадратичной формы. Найдите матрицу квадратичной формы:
- •Сколько линейно независимых собственных векторов может иметь матрица порядка 3*3
- •Покажите, что собственные векторы, отвечающие различным собственным значениям симметрической матрицы, ортогональны.
- •Сформулируйте теорему о приведении квадратичной формы к главным осям.
- •Приведите форму к нормальному виду методом Лагранжа.
- •Сформулируйте закон инерции квадратичных форм. Можно ли квадратичную форму с помощью невырожденного линейного преобразования переменных привести к виду ? Ответ обоснуйте.
- •Сформулируйте и проиллюстрируйте на примере критерий Сильвестра положительной определенности квадратичной формы от трех переменных.
- •8. Прямые и плоскости в точечном пространстве
- •Что представляет собой пересечение двух ортогональных плоскостей в ? Ответ обоснуйте и приведите пример.
- •9. Кривые второго порядка
- •Запишите общее уравнение линии второго порядка. Какое геометрическое место точек определяется уравнением ?
- •Дайте определение окружности и выведите ее каноническое уравнение.
- •Напишите уравнение окружности с центром в точке радиуса . При каком значении параметра , уравнение определяет окружность?
- •Как по каноническому уравнению эллипса определить, является ли он окружностью? Ответ обоснуйте.
- •Дайте определение гиперболы. Каков геометрический смысл параметров, входящих в каноническое уравнение гиперболы? Среди линий , , выберите гиперболы и постройте их.
- •Напишите каноническое уравнение гиперболы. Приведите пример уравнения гиперболы, не пересекающей ось абсцисс. Нарисуйте ее.
- •Являются ли параболами линии, заданные уравнениями: , ? Ответ обоснуйте.
- •Дайте определение кривой второго порядка. Какие кривые второго порядка задают уравнения , ? Изобразите их.
- •Какая из кривых второго порядка обладает асимптотами? Напишите каноническое уравнение этой линии и уравнения ее асимптот.
- •10. Выпуклые множества в точечном пространстве
- •Как задать луч, отрезок в точечном пространстве ? Приведите примеры.
- •Дайте определение выпуклого множества. Докажите, что пересечение выпуклых множеств является выпуклым.
- •Является ли множество точек , удовлетворяющих условию , выпуклым? Ответ обоснуйте.
- •Является ли множество точек удовлетворяющих условию , выпуклым? Ответ обоснуйте.
- •Приведите примеры выпуклого множества: а) имеющего угловую точку; б) не имеющего угловой точки. Может ли не ограниченное выпуклое множество иметь угловую точку? Приведите пример.
- •Дайте определение выпуклой оболочки системы точек. Пусть - выпуклая оболочка точек , , , . Принадлежат ли множеству точки: , ? Ответ обоснуйте.
- •11. Задачи линейного программирования
- •Приведите пример задачи линейного программирования, имеющей единственное решение. Ответ обоснуйте.
- •Приведите пример задачи линейного программирования, множеством оптимальных решений которой является отрезок. Ответ обоснуйте.
- •Приведите пример задачи линейного программирования, множеством оптимальных решений которой является луч. Ответ обоснуйте.
- •Приведите к стандартной форме задачу линейного программирования, уменьшив число переменных:
- •Приведите к канонической форме задачу линейного программирования:
- •Приведите пример задачи линейного программирования и постройте для нее двойственную задачу.
-
Дайте определение ортогонального базиса в . Приведите пример ортогонального базиса в , не содержащего ни одного из векторов стандартного базиса , , . Ответ обоснуйте.
Ортогональный (ортонормированный) базис — ортогональная (ортонормированная) система элементов линейного пространства со скалярным произведением, обладающая свойством полноты. Ортогональный базис — базис, составленный из попарно ортогональных векторов. Этот базис линейно независим. Пример ортогонального базиса в R3: v1=(3;0;0), v2=(0;-2;0), v3=(0;0;3). Так как (v1, v2) = (v2, v3) = (v1, v3) = 0.
4. Матрицы и определители
-
Дайте определение ранга матрицы. Приведите примеры матриц порядка
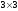 рангов 1, 2 и 3.
рангов 1, 2 и 3.
Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.
rg1 0 0
0 0 0 = 1
0 0 0
rg1 0 0
0 1 0 = 2
0 0 0
rg1 0 0
0 1 0 = 3
0 0 1
-
Дайте определение произведения матриц
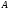 и
и
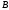 .
Приведите пример, когда
.
Приведите пример, когда
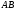 определено, а
определено, а
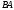 - нет. Существуют ли ненулевые квадратные
матрицы
- нет. Существуют ли ненулевые квадратные
матрицы
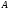 и
и
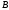 такие, что
такие, что
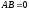 ?
Ответ обоснуйте.
?
Ответ обоснуйте.

-
Укажите, какие из равенств не выполняются для любых матриц
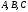 порядка
порядка
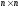 :
а)
:
а)
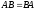 ;
б)
;
б)
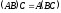 ;
в)
;
в)
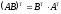 ;
г)
;
г)
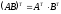 .Приведите
примеры, опровергающие неверные
равенства.
.Приведите
примеры, опровергающие неверные
равенства.

-
Укажите, какие из равенств не выполняются для любых обратимых матриц
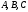 порядка
порядка
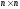 и ненулевого числа
и ненулевого числа
 :
а)
:
а)
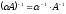 ;
б)
;
б)
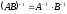 ;
в)
;
в)
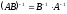 ;
г)
;
г)
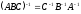 ?
Приведите примеры, опровергающие
неверные равенства.
?
Приведите примеры, опровергающие
неверные равенства.
-
Дайте определения вырожденной и невырожденной квадратных матриц порядка
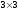 .
Приведите примеры таких матриц.
.
Приведите примеры таких матриц.
Квадратная матрица A ∈ Rn×n называется вырожденной, если detA = 0. В противном
случае матрица A называется невырожденной.
вырожденная: det0 1 0 0= 0
невырожденная:
det0 1 −1 0= 1
-
Сформулируйте основные свойства определителей, связанные с элементарными преобразованиями строк.
1) Если какая либо строка определителя состоит из 0, то и сам определитель равен нулю.
2)При перестановке любых 2-х строк определ.умножается на -1.
3) Определ. с 2 равными строками равен 0.
4) Общий множитель эл-тов любой строки можно вынести за знак определ.
5) Если эл-ты некоторых строк определ. представлены в виде суммы 2-х слагаемых, то и сам определ. равен сумме 2-х определ. 1и2. В определ. 1 указанная строка состоит из первых слагаемых в 2 из вторых.Остальные строки определ. 1и2 те же,что и в начальном.
6) Величина определ. не изменяется, если к одной из строк пребавить другую строку, умноженную на какое угодно число.
7)Сумма произведений эл-тов любой строки на алгебраич. дополнения к соответств. эл-там другой строки равен0.
8) Определю матрицы A равен определителю транспонир. матрицы |A|=|At|.
9)Определитель произведения 2-х матриц равен произведению определ. этих матриц, |A*B|=|A|*|B|.
-
Напишите разложение определителя
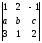 по второй строке.
по второй строке.
Ответ: -5a+5b+5c
-
Проверьте справедливость свойства
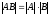 для матриц
для матриц
 ,
,
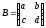 .
.
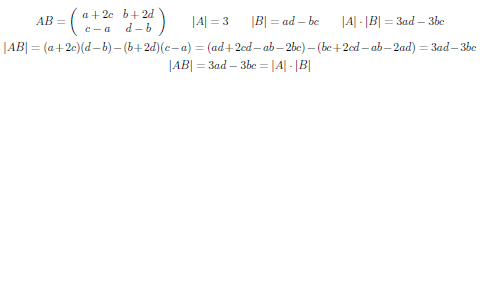
-
Докажите, что
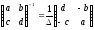 ,
где
,
где
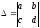 .
.
Докажем,
что

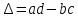
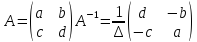
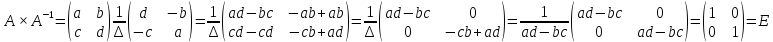
-
Существуют ли матрицы
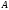 и
и
 такие, что
такие, что
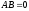 ,
а
,
а
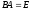 .
Ответ обоснуйте.
.
Ответ обоснуйте.
Предположим, что ∃A,B : AB = 0, BA = E. Тогда по свойству определителей
0 = |0| = |AB| = |A| · |B| = |B| · |A| = |BA| = |E| = 1. Пришли к противоречию, которое опровергает возможность существования таких матриц A и B.
-
Приведите формулу для вычисления обратной матрицы для матрицы порядка 3. С помощью этой формулы найдите
 .
.
-
Верно ли, что матричные равенства
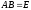 и
и
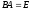 равносильны? Ответ обоснуйте.
равносильны? Ответ обоснуйте.

-
Сформулируйте правило Крамера для решения системы линейных уравнений
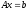 .
Докажите правило Крамера для системы
линейных уравнений от двух переменных.
.
Докажите правило Крамера для системы
линейных уравнений от двух переменных.

-
Проиллюстрируйте применение правила Крамера для решения системы уравнений
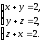
Ответ: x=1, y=1, z=1
