
- •1. Дайте определение предела послед-и. Приведите примеры: а) послед-и, сходящейся к числу 3; б) ограниченной послед-и, не имеющей предела.
- •3. Докажите, что сходящаяся послед-ь имеет только один предел
- •9. Дайте определение бесконечно малой (бм) послед-и. Приведите примеры бм послед-ей, отношение которых: а) является бм послед-ью; б) не является бм послед-ью.
- •10. Докажите, что произведение бм и ограниченной послед-ей является бм послед-ью.
- •13. Всякая ли неограниченная послед-ь является бесконечно большой? Ответ обоснуйте.
- •14. Приведите пример двух бесконечно больших послед-ей, сумма которых является бесконечно малой послед-ью.
- •15. Дайте определение убывающей послед-и. Что можно сказать о пределе убывающей послед-и, если она: а) ограничена снизу; б) не ограничена? Ответ обоснуйте.
- •17. Докажите, что предел суммы двух функций равен сумме их пределов, если последние существуют.
- •32. Следует ли из существования производной функции в точке ее непрерывность в этой точке?
- •34. Сформулируйте и докажите теорему о производной произведения двух функций.
- •40. Докажите, что эластичность произведения двух функций равна сумме их эластичностей.
- •41. Дайте опред и сформул необх усл лок экстремума ф-ии одной переменной. Прив прим ф-ии, для котор это усл выполнено в нек т, но экстремум отсутствует.
- •45. Сформулируйте теорему Коши для пары дифференцируемых функций. Выведите из этой теоремы утверждение теоремы Лагранжа.
- •62. Дайте определение однородной функции нескольких переменных. Приведите пример однородной функции f (X, y) степени 3, не являющейся рациональной функцией.
- •70. Дайте определение выпуклого множества в Rn . Приведите примеры выпуклых множеств в r2 , объединение которых: а) является выпуклым множеством; б) не является выпуклым множеством.
- •71. Докажите, что пересечение двух выпуклых множеств u , V . R2 является выпуклым множеством.
- •73. Дайте определение первообразной. Может ли первообразная иметь точку разрыва?
- •77. Докажите формулу интегрирования по частям для неопределенного интеграла.
- •78. Докажите формулу замены переменной для неопределенного интеграла.
- •82. Используя свойство интеграла с переменным верхним пределом, докажите формулу Ньютона - Лейбница для определенного интеграла.
- •83. Докажите, что для любых непрерывных на отрезке [a,b] функций f (X) и g(X) справедливо равенство
- •91. Дайте определения числового ряда и его суммы. Найдите сумму ряда
- •92. Рассмотрев последовательность частичных сумм ряда, докажите, что при ряд расходится.
- •93. Может ли ряд cходиться, если ряд сходится, а ряд
- •96. Докажите, что для сходимости ряда n, необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена.
- •97 Сформулируйте и докажите признак Даламбера для числовых рядов с положительными членами.
- •98 Сформулируйте признак Даламбера в предельной форме. Приведите пример сход ряда с положит членами, к кот этот признак применим.
- •100 Сформулируйте признак Лейбница для знакочеред числовых рядов. Приведите пример знакочеред ряда, сход условно.
- •114 Дайте определение лин дифф ур 2 ого порядка. Док-те, что если y1(X) и y2(X) решения лнду, то их разность y1(X)-y2(X) явл решением соответ дифф Ур-я.
45. Сформулируйте теорему Коши для пары дифференцируемых функций. Выведите из этой теоремы утверждение теоремы Лагранжа.
Пусть функции f(x) и g(x)
-
непрерывны на отрезке [a, b];
-
дифференцируемы в интервале (a, b);
"x О (a, b) g'(x) ≠ 0 .
Тогда существует точка c О (a, b) такая, что
![]() .
.
Частным случаем теоремы Коши (при g(x) = x) является теорема Лагранжа.
№46
Дайте определение многочлена Тейлора
ф-ции f(x)
в точке x0.
Чему равны его производные в этой точке?
Укажите какой-либо многочлен P(x),
удовлетворяющий условиям:
![]() .
.
Пусть
ф-ция f(x)
имеет n
производных в точке x0.
Многочлен
![]() называется
n-многочленом
Тейлора ф-ции f(x)
в точке x0.
называется
n-многочленом
Тейлора ф-ции f(x)
в точке x0.
Найдем производные:
![]()
![]()
аналогично
![]()
таким образом, для любого n, от 1 до к, выполняется равенство:
![]()
Пример:
![]()
№47Разлож
ф-цию
![]() по
формуле Маклорена до
по
формуле Маклорена до
![]() .
.
№48
Разложите ф-цию
![]() по
формуле Маклорена до
по
формуле Маклорена до
![]() .
.
№49
Дайте определение расстояния![]() между точками
между точками
![]() .
Сформулируйте и докажите свойства
функции
.
Сформулируйте и докажите свойства
функции
![]() .
.
Пусть
![]() .
Расстоянием между a
и b
называется число
.
Расстоянием между a
и b
называется число
![]() .
Расстояние между точками удовлетворяет
следующим свойствам:
.
Расстояние между точками удовлетворяет
следующим свойствам:
-
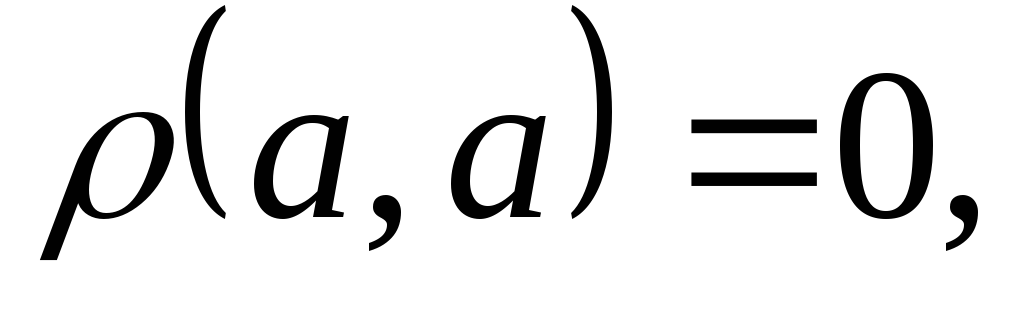 и
и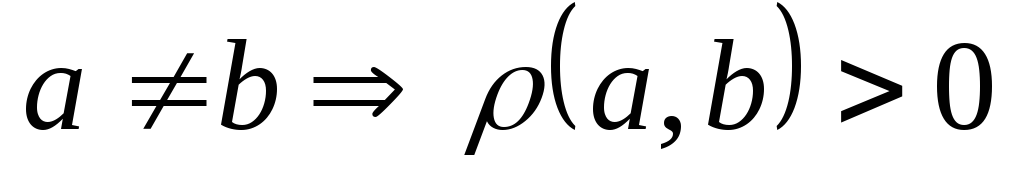
-
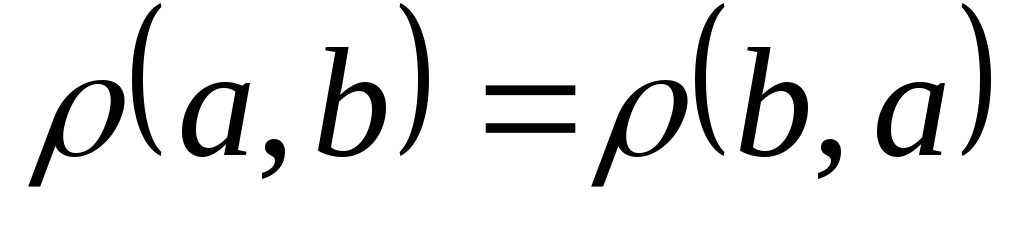
-
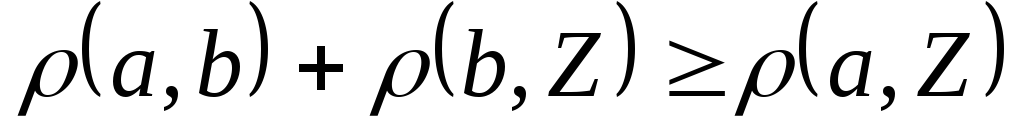
Доказательство
1 и 2 очевидно. Докажем 3. доказательство
носит название «неравенство треугольника».
Заметим, что пара точек
![]() определяет вектор
определяет вектор
![]() .
.
![]()
Проведём серию равносильных преобразований
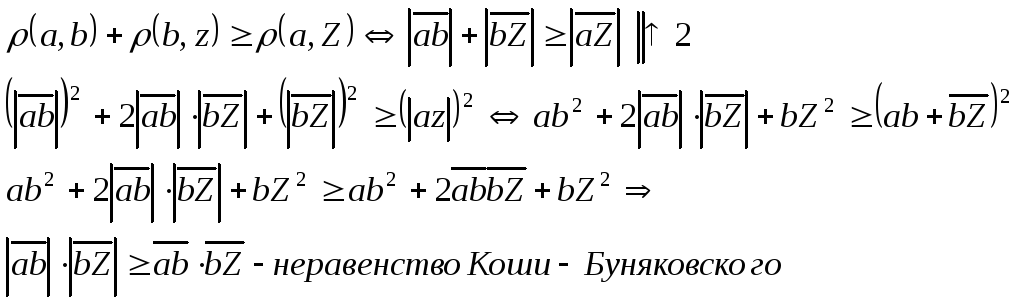
№50
Дайте определение открытого множества
в
![]() .
Явл ли множество
.
Явл ли множество
![]() замкнутым?
замкнутым?
Множество D называется открытым, если все его точки внутренние (замкнутым, если оно содержит все свои граничные точки).
Данное множество нельзя назвать замкнутым, так как оно не включает свою граничную точку «0».
№51
Дайте определение замкнутого множества
в
![]() .
Является ли множество
.
Является ли множество
![]() замкнутым.
замкнутым.
Множество {M} называется замкнутым, если все граничащие точки принадлежат этому множеству. Данное множество нельзя назвать замкнутым, так как оно не включает свою граничную точку «0».
№52 Дайте определение предельной точки множества. Приведите примеры множества а) содержащего все свои предельные точки; б) для которого существует предельная точка, ему не принадлежащая.
Точка М0 называется предельной точкой множества {M}, если в любой ее окрестности существуют точки множества {M}, отличные от М0
А)
![]() - множество, содержащее все свои предельные
точки
- множество, содержащее все свои предельные
точки
Б)
![]() является предельной, но множеству D
не принадлежит (множество, для которого
существует предельная точка, ему не
принадлежащая)
является предельной, но множеству D
не принадлежит (множество, для которого
существует предельная точка, ему не
принадлежащая)
№53
Дайте определение сходящейся
последовательности точек в
![]() .
К какой точке в
.
К какой точке в
![]() сходится
последовательность
сходится
последовательность
![]() ?
?
Последовательность точек {Mn}пространства Rn называется сходящейся, если существует такая точка А, что >0, N, nN, все точки этой последовательности будут сходиться в -окрестности точки А: (Mn ;A)<
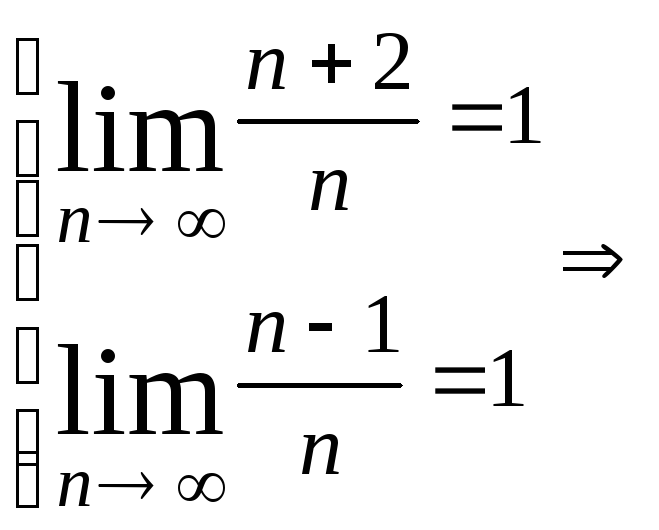 последовательность
сходится к точке (1,1)
последовательность
сходится к точке (1,1)
№54
Дайте определение предела ф-ции двух
переменных в точке. Найдите предел ф-ции
![]() в
точке (0,0).
в
точке (0,0).
b- предел функции f(M) в точке А, если >0, >0, что M, принадлежащей {Mn} из -окрестности точки А, т.е. (M;A)< , что выполняется неравенство: |f(M) - b| <,
limf(M)=b MA
![]() по
теореме о произведении бесконечно малой
на ограниченную ф-ции.
по
теореме о произведении бесконечно малой
на ограниченную ф-ции.
№55
Докажите, что ф-ция
![]() не
имеет предела в точке (0,0).
не
имеет предела в точке (0,0).
![]() Рассмотрим
2 последовательности точек из D(f),
сходящихся к точке (0,0).
Рассмотрим
2 последовательности точек из D(f),
сходящихся к точке (0,0).

Тогда
рассмотрим последовательность
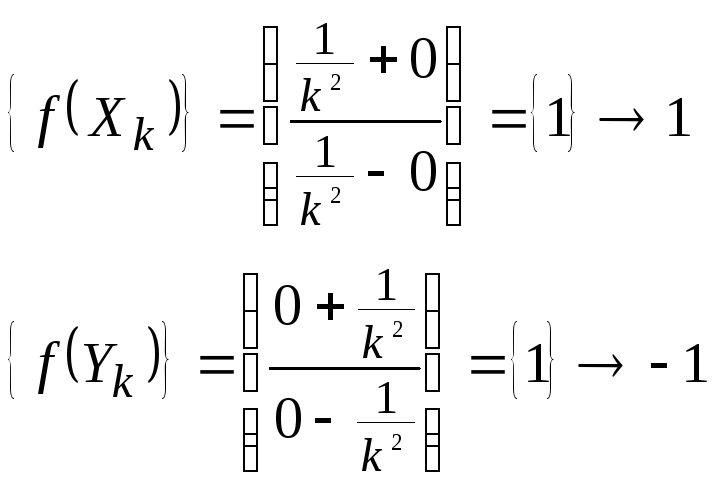
По определению предела данной ф-ции в точке (0;0) не существует.
№56
Дайте определение ф-ции двух переменных,
непрерывной в точке. Является ли ф-ция
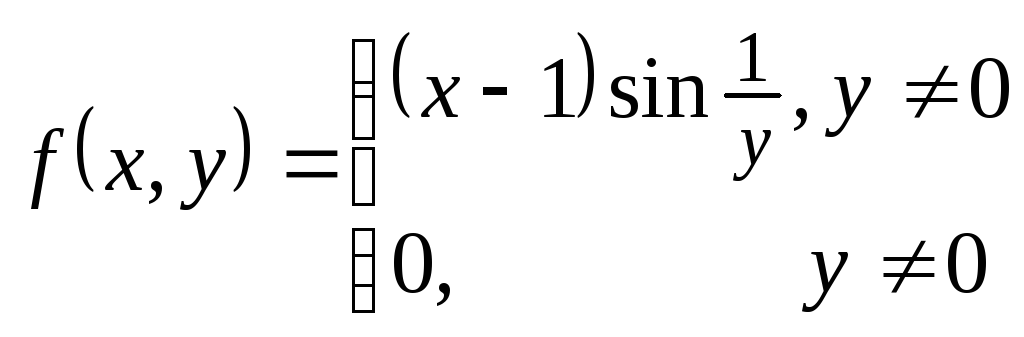 непрерывной
в точке (1,0)?
непрерывной
в точке (1,0)?
Функция u=f(M) называется непрерывной в точке А, если предел этой функции существует и равен значению функции в этой точке: limf(M)=f(A) MA
![]()
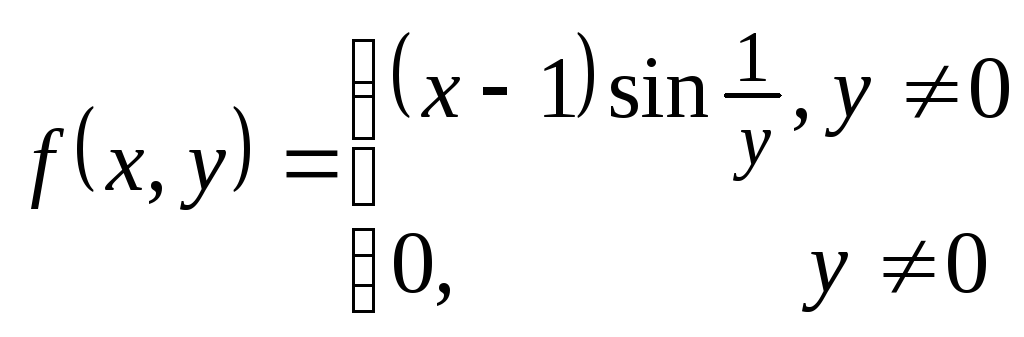
непрерывна в точке (1,0)?
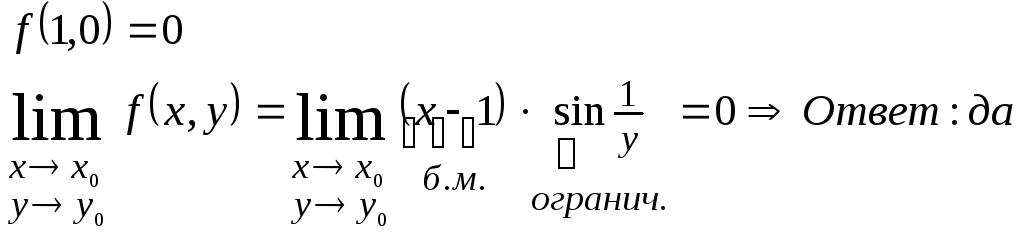
№57
Дайте определение частной производной
ф-ции f(x,y) по y в точке
![]() .
Найдите
.
Найдите
![]() ,
если
,
если
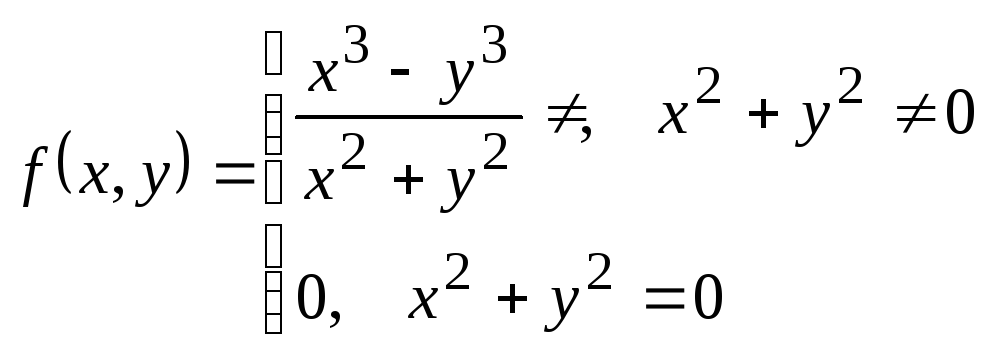
Частной производной по у функции z=f(x;y) называется предел отношений приращения ∆yz к приращению ∆у, при ∆у→0.
Zَx=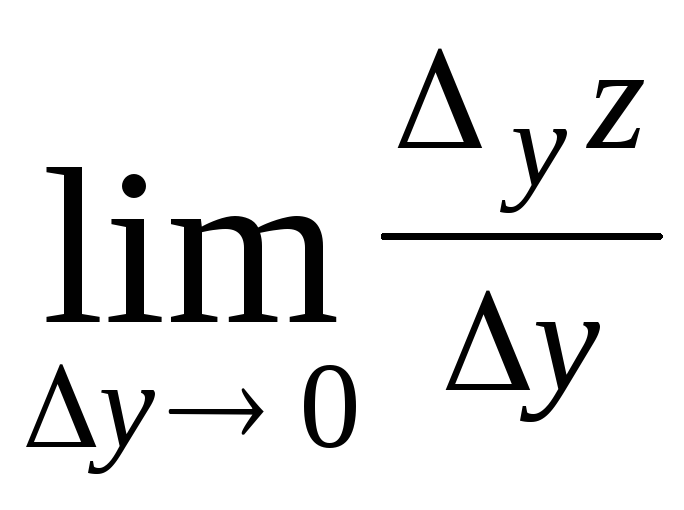 =lim(x0
; y0+∆y)-f(x0
;y0)/∆y,
x=const
=lim(x0
; y0+∆y)-f(x0
;y0)/∆y,
x=const
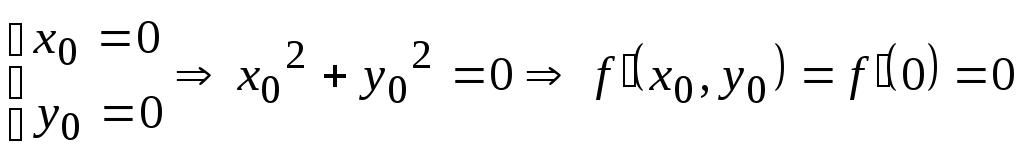
№58 Дайте определение дифференцируемости ф-ции f(x,y) в точке. Докажите, что если ф-ция дифференцируема в точке, то она непрерывна в этой точке.
Ф-ция
z=
f(x,y)
называется дифференцируемой в точке
M,
если её полное приращение в этой точке
может быть представлено в виде
![]() ,
где
,
где
![]() - б.м. ф-ция при
- б.м. ф-ция при
![]() .
.
![]()
=> ф-ция z=f(x,y) непрерывна в точке (х0;y0).
№59 Как связаны производная по направлению и градиент дифференцируемой ф-ции f(x,y)? Чему равна производная по направлению, перпендикулярному градиенту?
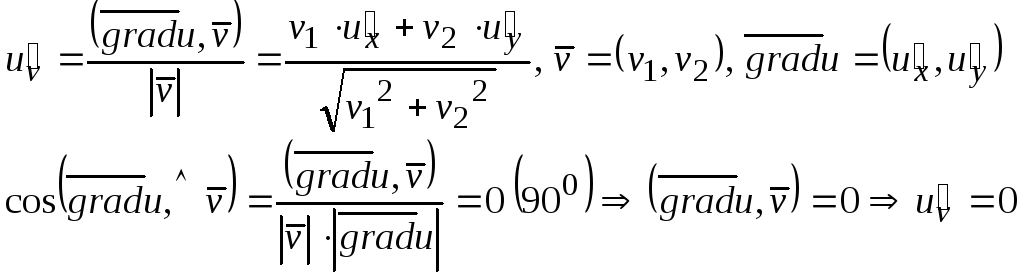
№60 Дайте определение градиента ф-ции f(x,y) в точке (х0;y0). Докажите, что в направлении градиента происходит наиболее быстрый рост ф-ции. Чему равна скорость этого роста?
Градиентом
ф-ции z=
f(x,y)
в точке M(x,y)
называется вектор, координаты которого
равны соответствующим частным производным
![]() ,
взятым в точке M(x,y).
,
взятым в точке M(x,y).
Градиент указывает направление наискорейшего роста функции, а максимальная скорость равна модулю градиента.
По
определению скалярного произведения
![]() .
Учитывая, что
.
Учитывая, что
![]() .
Из последнего следует, что производная
по направлению имеет наибольшую величину
при
.
Из последнего следует, что производная
по направлению имеет наибольшую величину
при
![]() ,
то есть когда направление вектора
,
то есть когда направление вектора
![]() совпадает
с направлением
совпадает
с направлением
![]() .
Скорость роста равна модулю градиента.
.
Скорость роста равна модулю градиента.
61. Дайте определение однородной функции степени . Является ли функция f(x;y) = (х2 +3ху)/(2х7 у –у8 ) однородной и, если да, то какой степени?
Функция z(x;y) называется однородной степени , если для любой точки (х;у) из области определения и переменной t выполняется равенство z(tx;ty)= t z(x;y).
Функция f (x, y)= (x2+3xy)/(2x7y-y8) является ли однородной?
F (tx, ty)= (t2x2+3tx*ty)/(2t7x7*ty-t8y8)=t2(x2+3xy)/t8(2x7y-y8)=t-4(x2+3xy)/(2x7y-y8)
Следовательно, данная функция является однородной степени -4.
