17. Докажите, что предел суммы двух функций равен сумме их пределов, если последние существуют.
(не совсем с функциями связано, но то же свойство, вроде, может подойдет, что-то другого ничего нету)
Пусть a и b – соответственно пределы {Xn} и {Yn}. Тогда Xn = a + αn, Yn = b + βn, где {αn} и {βn} – бм послед-и. Следовательно, (Xn±Yn) – (a±b) = αn ± βn.
Послед-ь {αn ± βn} – бм. Таким образом, послед-ь {(Xn±Yn) – (a±b)} также бм и поэтому послед-ь (Xn±Yn) сходится и имеет своим пределом число a±b.
18. Докажите, что функция f(x) = sin 1/x не имеет предела в точке x = 0.
lim (x→0) sin 1/x по Гейне lim (n→∞) Xn = X0, lim(x→0+0) 1/x = +∞, lim(x→0-0) 1/x = - ∞
lim (x→0+0) sin 1/x – не сущ. sin (x→0-0) 1/x – не сущ.
19. Дайте определение предела функции при x→+∞. Докажите, что функция f(x) = cosx не имеет предела при x→+∞.
-
Пределом функции f(x) при x→+∞ называют число а, если для любой послед-и {Xn} значений аргумента, послед-ь {f(Xn)} значений функции сходится к пределу а: lim (x→∞) f(x) = a.
2) f(x) = cosx => limx→+∞cosx=(-1;+1)
20. Дайте определения односторонних пределов функции в точке. Что можно сказать об односторонних пределах функции f(x) в точке X0, если известно, что lim (x→x0) f(x) = 3? Ответ обоснуйте.
1) Число b называется правым пределом f(x) в точке А, если для любой послед-и значений аргумента Xn, сходящихся к А и состоящих из чисел больше А (справа), соответствующая послед-ь значений функции сходится к числу b.
Число с называется левым пределом f(x) в точке А, если для любой послед-и значений аргумента Xn, сходящихся к А и состоящих из чисел меньше А (слева), соответствующая послед-ь значений функции сходится к числу с.
lim (x→a+0) f(x) = b; lim (x→a-0) f(x) = c
2) В случае Lim (x→ х0) f(x)=3 односторонние пределы тоже устремлены к 3. Обоснованием является существование данного предела в точке. Теорема: Функция f(x) имеет предел в точке x0 тогда и только тогда, когда в этой точке сущ. пределы слева и справа (они должны быть равны).
23. Дайте определение функции, непрерывной в точке. Найдите значение а, при котором функция f(x) = x arctg (1/x), x≠0, является непрерывной в точке x=0.
a, x = 0
Функция f(x), определенная в некоторой окрестности точки x0, называется непрерывной в этой точке, если предел функции в точке x0 существует и равен значению в этой точке:
lim (x→ x0) f(x) = f(x0)
является
непрерывной в точке x
= 0
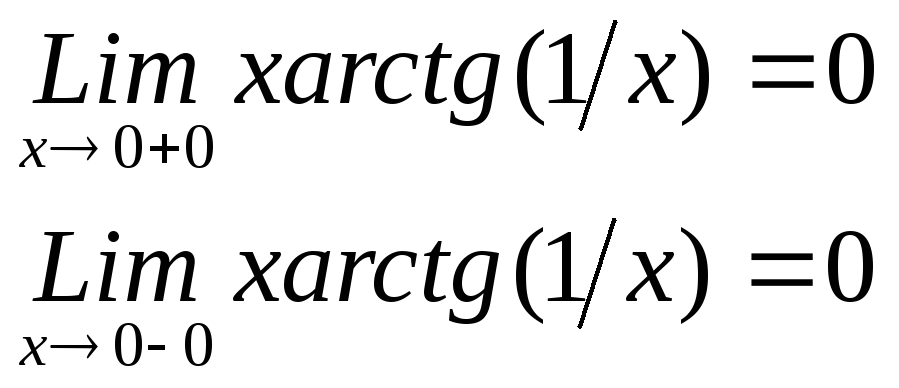следовательно
следовательно
а=0
24. Дайте опред точки разрыва ф-ии. Прив примеры функций, для которых x=0 является: а) т разрыва I рода со скачком, равным 9; б) т разрыва II рода.
Если в точке X0 функция f(x) не является непрерывной, то говорят, что f(x) разрывна в этой точке. Точку X0 называют точкой разрыва функции f(x), причем функция f(x) может быть не определена в точке X0.
1)Разрыв первого рода. Точка x0 называется точкой разрыва первого рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу правый и левый пределы:
2)Разрыв второго рода. Точка x0 называется точкой разрыва второго рода, если в этой точке функция f(x) не имеет по крайней мере одного из односторонних пределов или если хотя бы один из односторонних пределов бесконечен.
a) точка разрыва I рода со скачком, равным 9:
y = 4,5x/ |x| f(x) = x² + 9, x>0
x, x≤0
б) точка разрыва II рода:
y = 1/x точка x=0 – точка разрыва для функции.
25. Сформулируйте теорему о существовании нуля непрерывной функции. Используя эту теорему, докажите, что уравнение 5x2 + 4x - 5 = 0 имеет не менее двух действительных корней на отрезке [-1;1].
Если функция f(x) непрерывна на отрезке [a,b] и принимает на его концах значения разных знаков, то по крайней мере 1 раз функция обращается в нуль на этом отрезке.
5x2 + 4x - 5 = 0, f(-1)=0.25 , f(1)=4, , f(0)=-4
На концах отрезка [-1;1] функция принимает значения одинакового знака. Поделим данный отрезок на два отрезка [-1;0] и [0;1]. На концах отрезка [-1;0] функция принимает значения разных знаков, поэтому по теореме о существовании нуля непрерывной функции существует точка Aє[-1;0], в которой f (A)=0 (аналогично на другом отрезке). Получается, что данное уравнение имеет не менее двух действительных корней на отрезке [-1;1]
Дайте определение производной функции в точке. Найдите, исходя из
определения, производную функции f(x) в точке x0:
26. f(x) = x3, x0 - произвольное число.
Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0.
f
’(x)=
=
f(x) = x3
f
′(xо)=
=
=
=
=3
27. f(x)=sinx, xо-произвольное число
Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0.
f
’(x)=
=
f
′(xо)=
=
=
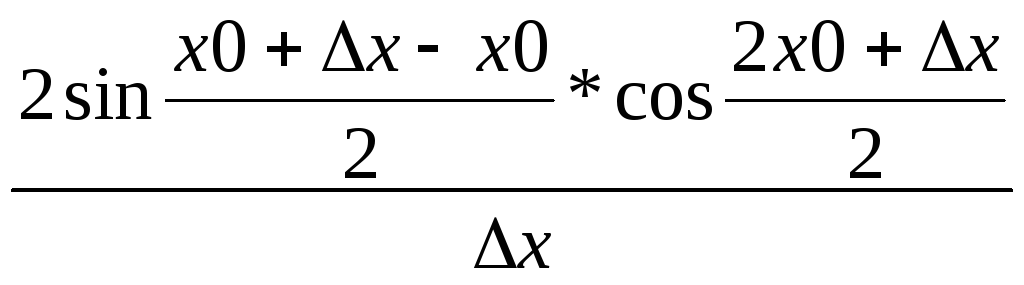=cosx0
28.
f(x)=
,
xо
=9
Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0.
f
’(x)=
=
f
’(x)=
=
=
=1/6
29.
f(x)=
,
xо
=1
Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0.
f
’(x)=
=
f
’(x)=
=
=
=
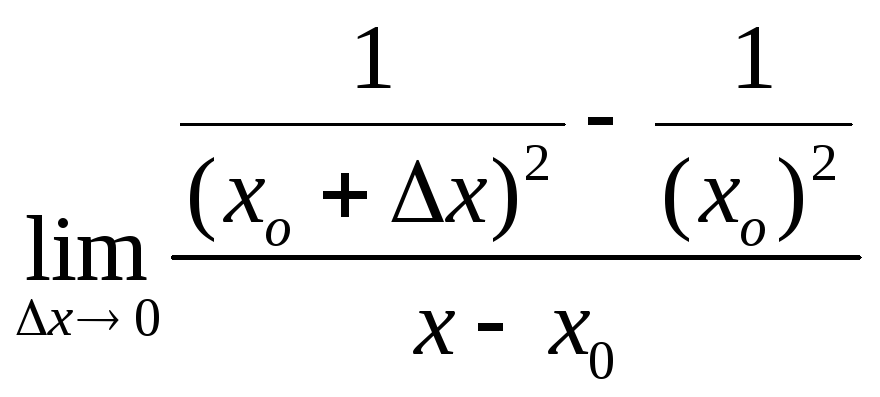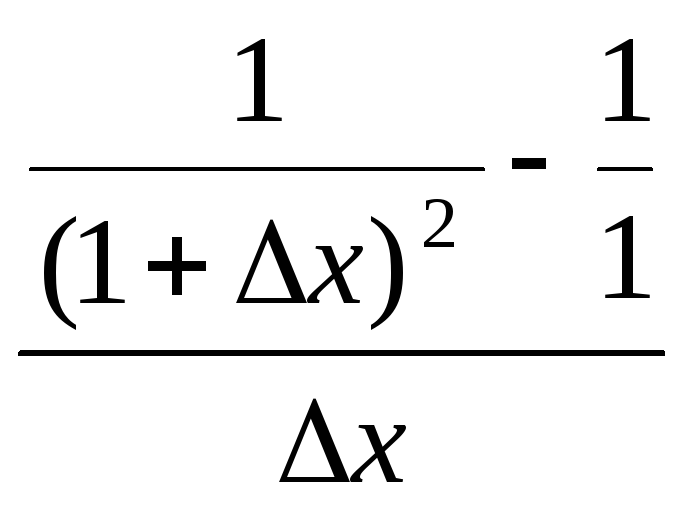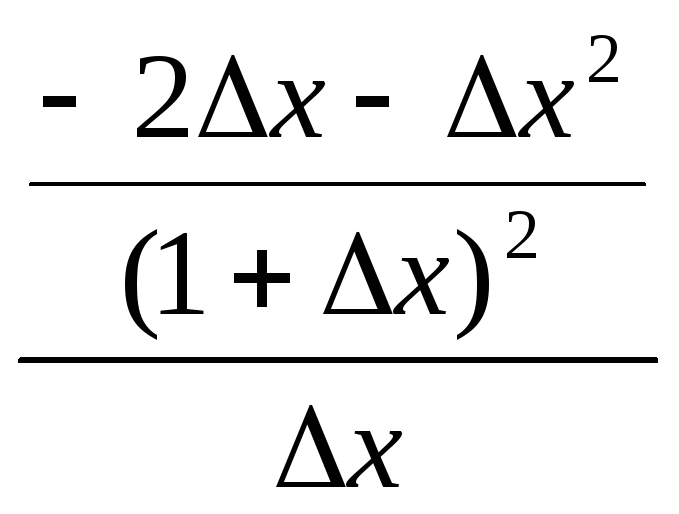=-2
30. f(x)=xx, x0=0
Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0.
f
’(x)=
=
31.
Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0.
f
’(x)=
=
