3. Тема 8. Конъюнктивная нормальная форма(кнф)

▪ Элементарная конъюнкция.

▪ Конъюнктивная нормальная форма.

▪ Минимальная КНФ. Два правила поглощения.

▪ Совершенная конъюнктивная нормальная форма(СКНФ).

▪ Два способа получения КДНФ.

Определение 1. Элементарной дизъюнкцией п пере­менных называется дизъюнкция переменных или их от­рицаний.

Определение 2. Конъюнктивной нормальной формой (КНФ) формулы А называется равносильная ей форму­ла, представляющая собой конъюнкцию элементарных дизъюнкций.

Для любой формулы алгебры логики путем равносиль­ных преобразований можно получить ее КНФ, причем не единственную.

Например, для формулы имеем:

, то есть

КНФ A .

Но так как х˅х = х, у ˅ у = у, , 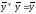то КНФ А = .

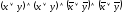А так как ,,

то КНФ A=.

Определение 3. КНФ А называется совершенной конъюнктивной нормальной формой формулы А ( СКНФ А ), если для нее выполнены условия:

1. Все элементарные дизъюнкции, входящие в КНФ А, различны.

2. Все элементарные дизъюнкции, входящие в КНФ А , содержат все переменные.

3. Каждая элементарная дизъюнкция, входящая в КНФ А, не содержит двух одинаковых переменных.

4. Каждая элементарная дизъюнкция, входящая в КНФ А, не содержит переменную и ее отрицание.

Каждая не тождественно истин­ная формула имеет единственную СКНФ.

Один из способов получения СКНФ состоит в исполь­зовании таблицы истинности для формулы .

Действительно, получив с помощью таблицы истин­ности СДНФ , мы получим СКНФ А , взяв отрицание , то есть СКНФ А = .

Другой способ получения СКНФ, использующий рав­носильные преобразования, состоит в следующем:

Путем равносильных преобразований формулы А получают одну из КНФ А.

Если в полученной КНФ А входящая в нее эле­ментарная дизъюнкция В не содержит переменную x_i,то, используя равносильность , элементар­ную дизъюнкцию В заменяют на две элементарные дизъ­юнкции В ˅ x_i и , каждая из которых содержит переменную x_i.

3. Если в КНФ А входят две одинаковых элементар­ных дизъюнкции В, то лишнюю можно отбросить, пользуясь равносильностью В˄ В = В .

4. Если некоторая элементарная дизъюнкция, входящая в КНФ А, содержит переменную x_i дважды, то лишнюю можно отбросить, пользуясь равносильностью x_i ˅ x_i = x_i.

5. Если некоторая элементарная дизъюнкция, вхо­дящая в КНФ А , содержит переменную x_i и ее отрицание, то = 1 и, следовательно, вся элементарная дизъюнкция имеет значение 1, а поэтому ее можно от­бросить, как единичный член конъюнкции.

Ясно, что после описанной процедуры будет получе­на СКНФ А.

Конъюнктивная нормальная форма(КНФ)

В результате изучения курса математической логики учащиеся должны:

- знать определение «элементарной конъюнкции», «конъюнктивной нормальной формы», «минимальной КНФ», «совершенной конъюнктивной нормальной формы(СКНФ)», два правила поглощения, два способа получения СКНФ;

- уметь находить КНФ, минимальную КНФ, СКНФ по заданной формуле и выполнять проверку полученного результата с помощью таблицы истинности.