8 Дисперсійний аналіз

Дисперсійний аналіз (від латинського Dіspersіo - розсіювання) – статистичний метод, що дозволяє аналізувати вплив різних факторів на досліджувану змінну. Метод був розроблений біологом Р. Фішером у 1925 році й застосовувався спочатку для оцінки експериментів у рослинництві. Надалі з'ясувалася загальнонаукова значимість дисперсійного аналізу для експериментів у психології, педагогіці, медицині та ін.

Задачею дисперсійного аналізу є визначення впливу одного або декількох факторів на ознаку, що вивчається.

Дисперсійний аналіз використовується, якщо залежна змінна числова, а незалежні, тобто ті, що впливають, мають нечислову природу.

Наприклад:

1. Порівняння показників міцності інструменту, виготовленого на різних заводах.

2. Вплив раціону корму на вагу тварин.

3. Вплив дизайну упакування на обсяг продажу.

Залежно від кількості факторів, включених в аналіз, розрізняють:

• однофакторний;

• двофакторний;

• багатофакторний.

Для проведення дисперсійного аналізу необхідно дотримуватися таких умов:

• результати спостережень повинні бути незалежними випадковими величинами;

• результати спостережень повинні мати нормальний розподіл;

• результати спостережень повинні мати однакову дисперсію.

Основною метою дисперсійного аналізу є дослідження значущості розбіжності між середніми груп. Необхідно відповісти на запитання, чи істотно фактор впливає на значення вибіркових середніх або ці розбіжності є несуттєвими. Іншими словами, якщо вибірки належать до однієї генеральної сукупності, то розкид даних між вибірками (між групами) повинен бути не більше, ніж розкид даних усередині цих вибірок (усередині груп).

Може здатися дивним, що процедура порівняння середніх має назву дисперсійний аналіз. Це пов'язано з тим, що при дослідженні статистичної значущості розбіжностей між середніми двох або декількох груп насправді аналізуються вибіркові дисперсії.

8.1 Однофакторний дисперсійний аналіз

Для найпростішого випадку таблиця вхідних даних має вигляд:

	Спостереження
Номер сукупності	1	2	...	n
1 2 . . . m	x11 x21 . . . xm1	x12 x22 . . . xm2	… … … … … …	x1n x2n . . . xmn

Це може бути, наприклад, m партій сировини і з кожної взято по n зразків. Необхідно з'ясувати, чи змінюються показники сировини від партії до партії.

Можна сказати, що ми досліджуємо m вибірок, обсяг кожної дорівнює n.

Будемо вважати, що для i-го рівня (для i-ї вибірки) n спостережень мають середню β_i, що дорівнює сумі загальної середньої для всіх випробувань μ і її варіації, яка обумовлена i-м фактором

β_i=μ+γ_i.

Тоді одне спостереження можна подати у вигляді

х_ij=μ+γ_i+ξ_ij=β_i+ξ_ij ,

де μ - загальна середня;

γ_i - ефект, обумовлений i-тим фактором;

ξ_ij – варіація результатів усередині однієї вибірки, характеризує вплив неврахованих факторів.

Відповідно до загальної задачі дисперсійного аналізу потрібно оцінити істотність впливу фактора γ на досліджувану величину.

Загальну варіацію x_ij можна розкласти на частини, одна із яких характеризує вплив фактора, інша – вплив неврахованих факторів.

Для цього необхідно знайти оцінку загальної середньої μ і оцінки середніх за рівнями β_i .

Оцінкою β_i є середнє арифметичне n спостережень i-го рівня:

.

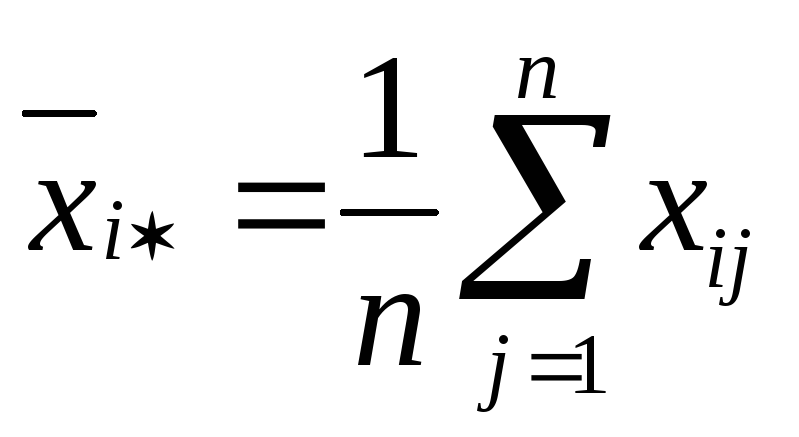Зірочка (*) в індексі означає, що спостереження, фіксовані на і-му рівні.

Оцінкою для μ є середнє арифметичне всієї сукупності:

.

Знайдемо суму квадратів відхилень від середніх

(8.1)

Розглянемо доданок

=0, оскільки це сума відхилень від середніх, а отже і S=0. Тоді (8.1) можна записати у вигляді

,

або

Q=Q₁+Q_2,

де Q₁ – сума квадратів відхилень вибіркових середніх від загального середнього (сума квадратів відхилень між групами), характеризує розбіжності між рівнями;

Q₂ – сума квадратів відхилень спостережуваних значень від вибіркового середнього (сума квадратів відхилень усередині груп), характеризує розбіжності усередині групи;

Q – загальна сума квадратів відхилень спостережуваних значень від загального середнього .

Знаючи Q, Q₁ , Q₂, можна оцінити відповідні дисперсії, тобто загальну, міжгрупову (факторну) і внутрішньогрупову (залишкову):

; ; ;

.

Звичайно розраховують Q і Q₁, а потім обчислюють

Q₂ = Q-Q₁.

Для того, щоб перевірити при заданому рівні значущості α гіпотезу про рівність середніх декількох (m>2) нормальних сукупностей з невідомими, але однаковими дисперсіями, досить перевірити за критерієм Фішера гіпотезу про рівність факторної й залишкової дисперсії S₁=S₂ .

Якщо вплив всіх рівнів фактора g однаковий, то S₁ і S₂ – оцінки загальної дисперсії, тому відрізняються незначуще.

Гіпотези:

Н₀ : S₁² = S₂²; H₁ : S₁² > S₂².

Розраховуємо F_р = , що має розподіл Фішера з k₁= m-1 і k₂ = m(n-1) ступенями вільності.

При заданому рівні значення a обчислюють критичне значення F_кр =F(a; k₁; k₂).

Якщо F_р > F_кр, то Н₀ відкидається й робиться висновок про істотний вплив фактора γ.

Якщо F_p < F_кр – немає підстави відкидати гіпотезу Н₀ і вважають, що вплив фактора γ несуттєвий.

Для більш повного розуміння, як будується F-статистика для перевірки гіпотези H₀ , запишемо

Порівнюючи міжгрупову та залишкову дисперсії, за величиною їх відношення судять, наскільки сильно проявляється вплив фактора.

Однофакторний аналіз зручно подавати у вигляді таблиці.

Компоненти дисперсії	Сума квадратів, (SS)	Число ступенів вільності, (DS)	Дисперсія (MS)
Міжгрупова		m-1
Внутрішньо- групова		m(n-1)
Загальна		mn-1

Приклад. Необхідно виявити, чи впливає відстань від центра міста на ступінь заповнюваності готелів. Нехай введені 3 рівні відстаней від центра міста: 1) до 3 км, 2) від 3 до 5 км і 3) понад 5 км. Дані заповнюваності представлені в таблиці.

Відстань	Заповнюваність
До 3 км	92 98 89 97 90 94
Від 3 до 5 км	90 86 84 91 83 82
Понад 5 км	87 79 74 85 73 77