Пункт 6

Функция плотности нормального распределения имеет вид:

f (x) =

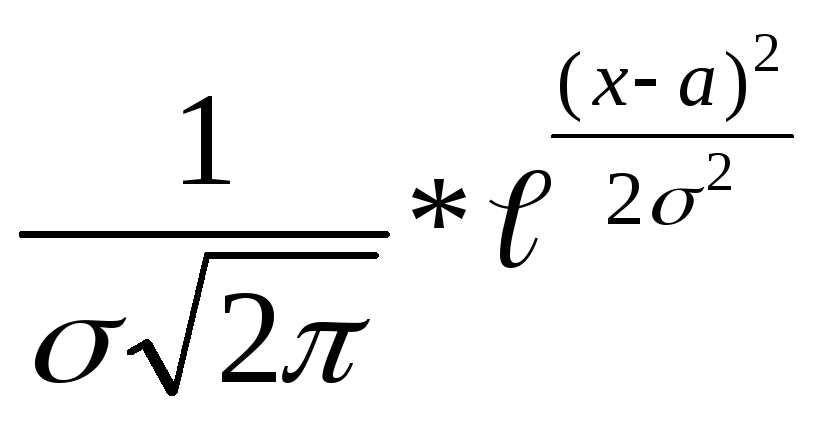
В качестве неизвестных параметров а и возьмем их точечные оценки = 50,57 и S_x=17,95 соответственно. Тогда дифференциальная f (x) и интегральная функции F(x) предполагаемого нормального закона распределения примут вид:

f (x) = ; F(x) =

Пункт 7

Гипотезу о том, что генеральная совокупность, из которой извлечена выборка, распределена по предлагаемому нормальному закону, назовем нулевой (Н₀ : ХN(a,)), тогда Н_а :ХN(a,). Проверим ее с помощью критерия согласия Пирсона.

Согласно критерию Пирсона сравниваются эмпирические n_i (наблюдаемые) и теориетические n*p_i (вычисленные в предположении нормального распределения) частоты. В качестве критерия проверки нулевой гипотезы принимается случайная величина

_набл =

По таблице критических точек распределения по заданному уровню значимости и числу степеней свободы (S – число интервалов, r – число параметров предполагаемого распределения СВ Х) находится критическое значение _кр(,).

Если _набл < _кр(,), то считается, что данный критерий не дает оснований для отклонения гипотезы при данном уровне значимости = 0,05. в противном случае считается, что гипотеза не согласуется с экспериментальными данными и ее нужно отвергнуть.

Если проверяется гипотеза о нормальном распределении, то вероятности p_i рассчитываются с помощью функции Лапласа Ф(х):

p_i = Р(х_i <Х< х_i+1) = Ф- Ф,

где х= 50,57, S_x=17,95.

р₁ = Р(-< х < 19,9 ) = Ф- Ф= Ф(-1,7) – Ф(-) = -Ф(1,7) + Ф() = -0,4554 + 0,5 = 0,0446

р₂ = Р(19,9 < х < 29,7 ) = Ф- Ф= Ф(-1,16) – Ф(-1,7) = -Ф(1,16) + Ф(1,7) = -0,3770 + 0,4554 = 0,0784,

р₃= Р(29,7 < х < 39,5 ) = Ф- Ф= Ф(-0,62) – Ф(-1,16) = -Ф(0,62) + Ф(1,16) = -0,2324 + 0,3770 = 0,1446,

р₄= Р(39,5 < х < 49,3 ) = Ф- Ф= Ф(-0,07) – Ф(-0,62) = -Ф(0,07) + Ф(0,62) = -0,0280 + 0,2324 = 0,2044,

p₅= Р(49,3 < х < 59,1 ) = Ф- Ф= Ф(0,48) – Ф(-0,07) = Ф(0,48) + Ф(0,07) = 0,1844 + 0,0280 = 0,2124,

p₆= Р(59,1 < х < 68,9 ) = Ф- Ф= Ф(1,02) – Ф(0,48) = 0,3462 - 0,1844 = 0,1618,

p₇= Р(68,9 < х < 78,7 ) = Ф- Ф= Ф(1,57) – Ф(1,02) = 0,4418 - 0,3462 = 0,0956,

p₈= Р(78,7 < х < 88,5 ) = Ф- Ф= Ф(2,11) – Ф(1,57) =0,4826 - 0,4418 = 0,0408,

р₉= Р(88,5 < х < 98,3 ) = Ф- Ф= Ф(2,66) – Ф(2,11) =0,4961 - 0,4826 = 0,0135.

Вычисления сведем в таблицу 4. количество интервалов S =9 .

Так как предполагается нормальное распределение имеющее два параметра (математическое ожидание а и среднее квадратическое отклонение ), поэтому r = 2, тогда число степеней свободы = S – r – 1 = 6.

Таблица 4

Интервалы (аi;ai+1]	Частоты эмпирические ni	Вероятности рi	Теоритические частоты n*рi	(ni - n*рi)2/n*рi
(10,1; 19,9]	4	0,0446	4,46	0,0474
(19,9; 29,7]	10	0,0784	7,84	0,5951
(29,7; 39,5]	14	0,1446	14,46	0,0146
(39,5; 49,3]	20	0,2044	20,44	0,0095
(49,3; 59,1]	19	0,2124	21,24	0,2362
(59,1; 68,9]	15	0,1618	16,18	0,0861
(68,9; 78,7]	13	0,0956	9,56	1,2378
(78,7; 88,5]	4	0,0408	4,08	0,0016
(88,5; 98,3]	1	0,0135	1,35	0,0907
	100	0,9961	99,61	2,319

Значение _набл =2,319.

В таблице критических точек распределения по уровню значимости = 0,05 и числу степеней свободы = 6 найдем критическое значение _кр(0,05;6) = 12.592

Так как _набл < _кр, то считаем, что нет оснований для отклонения нулевой гипотезы при заданном уровне значимости = 0,05.

Построим график эмпирической функции f (x). Для этого из середины частичных интервалов восстановим перпендикуляры высотой равной p_i – вероятностям попадания CB X в соответствующий частичный интервал. На рис. 3 концы перпендикуляров отмечены точками, полученные точки соединены плавной кривой.

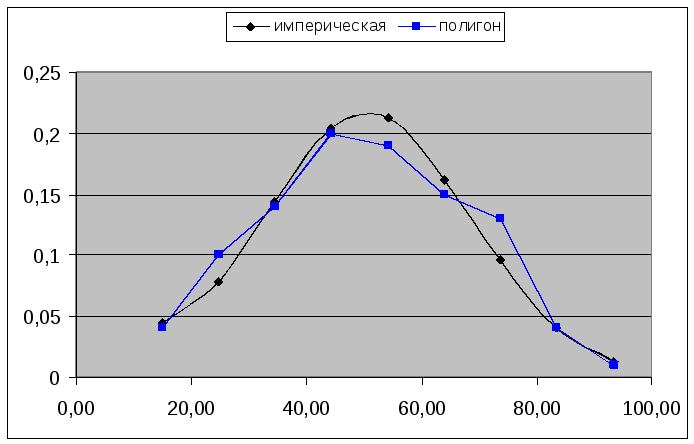
Рис. 3

Сравнение полигона относительных частот и нормальной кривой показывает, что построенная нормальная кривая удовлетворительно сглаживает полигон.