§5. Модуль действительного числа.

Определение: Модулем, или абсолютной величиной, числа называется число , равное самому , если неотрицательно, и равное (-, если - отрицательно:

Из определения модуля a ясно, что неотрицательное число. Отметим геометрический смысл абсолютной величины: – это расстояние между точками 0 и a на числовой прямой.

Легко проверить справедливость неравенств -Действительно, если то справа будет равенство, а левое неравенство очевидно. Если же , то слева будет равенство, а правое неравенство очевидно.

Модуль действительного числа обладает свойствами:

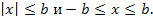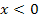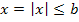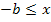1. Пусть b – положительное число, тогда равносильны неравенства В самом деле, пусть выполнено первое, тогда при , очевидно, и, кроме того, При , очевидно, т.е. Значит, выполнено второе. Пусть выполнено второе, тогда при имеем , а при из неравенств получаем 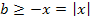, т.е. выполнено первое.

2. Модуль суммы двух чисел не превосходит суммы модулей:

.

Последнее неравенство принято называть неравенством треугольника. Такое название объясняется тем, что для векторов это неравенство означает сравнение длины одной стороны треугольника с суммой длин двух других сторон.

Для доказательства сложим почленно неравенства . Получим , но по предыдущему свойству это равносильно неравенству треугольника.

Методом математической индукции можно доказать справедливость более общего неравенства:

3. Модуль разности не меньше разности модулей данных чисел:

Действительно, . Отсюда и вытекает нужное неравенство.

Замечание: Если учесть, что , то для разности двух чисел справедливы неравенства:

.

Отметим геометрический смысл величины - это расстояние между точками a и b на числовой прямой.

4. Абсолютная величина произведения и частного равны соответственно произведению и частному абсолютных величин данных чисел:

Это свойство следует из определения абсолютной величины и правила знаков при умножении и делении.

§6. Числовые множества.

Как уже отмечалось, изучение множества действительных чисел равносильно изучению множества точек числовой оси. При этом понятия «число», «больше», «меньше» заменяются геометрическими понятиями «точка», «правее», «левее».

Введем теперь важные понятия, относящиеся к произвольным множествам числовой оси.

Определение 1. Множество называется ограниченным снизу, если Число a называется нижней границей множества E.

x

a

x

b

Рис. 4

Определение 2. Множество E называется ограниченным сверху, если . Число b называется верхней границей множества E.

Очевидно, что у ограниченного снизу множества существует бесконечно много нижних границ, а у ограниченного сверху множества – бесконечно много верхних границ.

Определение 3. Множество E называется ограниченным, если оно одновременно ограничено сверху и снизу, т.е.

.

Ясно, что для ограниченного множества можно указать такое , что для всех будет выполнено условие или

Определени 4. Число называется нижней гранью множества E, если оно является наибольшей из нижних границ множества E и обозначается . Иначе говоря, , если выполнены два условия:

1. 

2. .

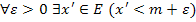Определение 5. Число M называется верхней гранью множества E, если оно является наименьшей из верхних границ множества E и обозначается . Иначе говоря, если выполнены два условия:

1. 

2. .

Например, множество ограничено и сверху и снизу. Для него причем

Множество ограничено только снизу и .

Неограниченное сверху/снизу множество можно определить, используя отрицание определения ограниченного сверху/снизу множества. Например, беря отрицание от формулы получим

Иначе говоря, множество E неограниченно сверху, если для любого числа b найдется такое число что

Например, множество неограниченно сверху и для любого b мы всегда можем указать такое число , что

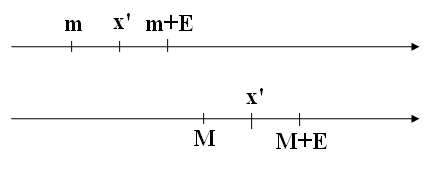
Рис. 5

Рассмотрим простейшие точечные множества на числовой прямой, которые принято называть промежутками.

1. Множество точек удовлетворяющих условию , называется замкнутым промежутком, или отрезком, и обозначается .

2. Множество точек , удовлетворяющих условию называется открытым промежутком, или интервалом, и обозначается .

Множество точек, удовлетворяющих условию или , называется полузамкнутым (полуоткрытым) промежутком, или полуинтервалом, и обозначаются, соответственно,

Далее, в математике часто приходится иметь дело с двумя способами присоединения к числовой системе бесконечных несобственных элементов.

1. Расширение с помощью символа .

Положим по определению:

;

- не имеет смысла;

если ;

– не имеет смысла;

Неравенства с не рассматриваются, т.к. бессмысленно спрашивать больше или меньше , чем конечное число.

2. Расширение с помощью символов - .

Положим по определению:

;

;

не имеет смысла;

;

лишены смысла.

В предположении, что основные свойства неравенств сохраняются и в расширенной числовой системе и, соответсвенно, числовые промежутки могут быть бесконечными. Так интервал (-) есть вся числовая ось; интервал есть множество точек x, удовлетворяющих условию a<x (лежащих справа от a), а интервал есть множество точек x, удовлетворяющих условию x<b (лежащих слева от b).

Общее обозначение для промежутков любой природы .

Теорема. Всякое непустое множество на числовой оси ограниченное снизу (сверху) имеет нижнюю (верхнюю) грань.

Доказательство. Покажем, что утверждение теоремы следует из теоремы Дедекинда. Пусть E – множество точек на числовой прямой ограниченное снизу. Через A обозначим множество всех нижних границ E, а через B – множество остальных точек оси. Множество A не пусто, так как E ограничено снизу, а B непусто, так как для по теореме Архимеда существует , т.е. . По определению B, множества A и B не пересекаются и Наконец, для любых и найдется такое, что (так как b не является нижней границей), но и поэтому

Итак, A и B образуют дедекиндово сечение.

Пусть число, производящее сечение. Покажем, что является искомой нижней гранью Е.

Предположим, что . Тогда найдется такое, что . По свойству плотности найдется число c такое, что . Правое неравенство здесь говорит о том, что , т.е. является нижней границей E, а левое неравенство этому противоречит. Следовательно, предположение о том, что , неверно и . Но тогда наибольшая из нижних границ, что и требовалось доказать.

Нетрудно видеть, что теорема Дедекинда в свою очередь вытекает из теоремы о существовании граней. Действительно, множества, образующие дедекиндово сечение, ограничены: одно – сверху, другое – снизу, а их грани совпадают и производят сечение. Отсюда следует, что эти теоремы эквивалентны.

Модуль 2. Функции.

Лекция 4