
- •Дисциплина «Математический анализ»
- •Раздел I. Введение в анализ
- •§1 Понятие множества. Теоретико-множественные отношения и операции. Декартово произведение.
- •Способы задания множеств
- •Теоретико-множественные отношения
- •Подмножества
- •Теоретико-множественные операции
- •§2 Множество действительных чисел.
- •§3. Изображение действительных чисел на прямой.
- •§4. Основные свойства множества действительных чисел.
- •§5. Модуль действительного числа.
- •Модуль действительного числа обладает свойствами:
- •§6. Числовые множества.
- •§7. Функции и их общие свойства.
- •§8. Действительная функция действительной переменной.
- •§9. Некоторые типы поведения действительных функций действительной переменной. Функции монотонные и кусочно-монотонные.
- •Функции четные и нечетные.
- •Периодические функции.
- •Функции ограниченные и неограниченные.
- •§10. Обратная функция.
- •§11. Числовые последовательности..
- •§12. Принцип вложенных отрезков.
- •§13. Бесконечные десятичные дроби.
- •§14. Предельная точка множества. Теорема Больцано-Вейерштрасса.
- •§15. Понятие предела числовой последовательности.
- •§16. Основные теоремы о пределах последовательностей.
- •§17. Предел монотонной последовательности. Число «e».
- •§18. Критерий Коши.
- •§19. Верхний и нижний пределы.
- •§20. Понятие предела функции.
- •§21. Основные теоремы о пределах функции в точке
- •§22. Предел функции по множеству. Предел на бесконечности.
- •§23. Первый замечательный предел.
- •§24. Второй замечательный предел.
- •§25. Бесконечно малые функции и их сравнения
- •§26 Бесконечно большие функции
§3. Изображение действительных чисел на прямой.
Геометрическое представление множества рациональных чисел может быть получено следующим образом. На некоторой прямой линии (рис.1) выбираем точку О в качестве начала отсчета, положительное направление и единичный отрезок – масштаб.
-3 -2 -1 1 2
3
O A











Рис.1
После этого выбора прямая называется числовой осью. Обычно числовую ось располагают горизонтально, а за положительное направление берут направление слева направо.
Целые
числа на числовой оси изображаются
точками, отстоящими от точки О на
соответствующее целое число единиц
масштаба, нуль изображается точкой О.
Если отрезки между этими точками
разделить на n
равных
частей, то получим точки, изображающие
рациональные числа ![]() .
Придавая n
всевозможные
натуральные значения, получим в результате
множество точек на числовой оси,
изображающих всевозможные рациональные
числа, или короче, множество рациональных
точек оси. Равные рациональные числа,
очевидно, изображаются одной и той же
точкой, а неравные – различными точками,
причем большее число изображается
точкой, лежащей правее.
.
Придавая n
всевозможные
натуральные значения, получим в результате
множество точек на числовой оси,
изображающих всевозможные рациональные
числа, или короче, множество рациональных
точек оси. Равные рациональные числа,
очевидно, изображаются одной и той же
точкой, а неравные – различными точками,
причем большее число изображается
точкой, лежащей правее.
Исчерпывают ли рациональные точки множество всех точек оси? Пусть отрезок OA является диагональю квадрата со стороной, равной единице масштаба.
Если
x
длина
отрезка
ОА
в единицах масштаба, то по теореме
Пифагора должно выполняться равенство
![]() .
Но, как было показано выше, x
не может быть рациональным числом.
Следовательно, точка A
не является рациональной, и множество
рациональных точек не заполняет всю
числовую ось.
.
Но, как было показано выше, x
не может быть рациональным числом.
Следовательно, точка A
не является рациональной, и множество
рациональных точек не заполняет всю
числовую ось.
Важным следствием введения иррациональных чисел является тот факт, что каждой точке числовой оси единственным образом соответствует некоторое действительное число и наоборот. Действительно, пусть A точка на числовой оси (рис.2) не является рациональной точкой.

![]()
![]()
![]()
![]()





A
Рис.2
Пусть
для определенности A
лежит
на положительной полуоси. Найдется
целое неотрицательное число ![]() такое, что A
лежит между точками
такое, что A
лежит между точками ![]() и
и
![]() .
Разделим отрезок между
.
Разделим отрезок между ![]() и
и
![]() на десять равный частей, найдем точки
на десять равный частей, найдем точки
![]() и
и ![]() между
которыми лежит точка A.
Аналогично найдем точки
между
которыми лежит точка A.
Аналогично найдем точки ![]() и
и ![]() и т.д. В результате этого процесса
найдется иррациональное число
и т.д. В результате этого процесса
найдется иррациональное число ![]() соответствующее точке А.
Верно и обратное, для каждого действительного
числа
соответствующее точке А.
Верно и обратное, для каждого действительного
числа ![]() можно найти соответствующую точку А
на
числовой оси.
можно найти соответствующую точку А
на
числовой оси.
Тесная связь между действительными числами и точками числовой оси приводит к тому, что в дальнейшем между понятиями «действительное число» и «точки числовой оси» не делается различия, а изучение числовых множеств становится равносильным изучению точечных множеств на оси.
§4. Основные свойства множества действительных чисел.
Приведем без доказательства совокупность
основных свойств множества ![]() .
Эта совокупность интересна тем, что
может быть принята за систему аксиом,
из которой как следствие выводится вся
теория действительных чисел.
.
Эта совокупность интересна тем, что
может быть принята за систему аксиом,
из которой как следствие выводится вся
теория действительных чисел.
-
Для любых
 однозначно
сопоставлен элемент из
однозначно
сопоставлен элемент из  ,
называемый суммой
,
называемый суммой  ,
причем для любых
,
причем для любых  :
:
-
 / коммутативность сложения/;
/ коммутативность сложения/; -
 /
ассоциативность сложения/;
/
ассоциативность сложения/; -
 /
свойство
нуля/;
/
свойство
нуля/; -
 /
свойство противоположного числа/;
/
свойство противоположного числа/;
Для
любых ![]() однозначно
сопоставлен элемент из
однозначно
сопоставлен элемент из ![]() ,
называемый произведением и обозначаемый
,
называемый произведением и обозначаемый
![]() ,
причем для любых
,
причем для любых ![]() :
:
-
 / коммутативность умножения/;
/ коммутативность умножения/; -
 / ассоциативность умножения/;
/ ассоциативность умножения/; -
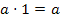 / свойство
единицы/;
/ свойство
единицы/; -
 / существование обратного числа/;
/ существование обратного числа/; -
Для сложения и умножения имеет место дистрибутивность, т.е. для любых


-
Для любых
 выполнено, по крайней мере, одно
неравенство: или
выполнено, по крайней мере, одно
неравенство: или  или
или
 ,
причем для любых
,
причем для любых  :
:
-
 /
рефлексивность/;
/
рефлексивность/; -
 и
и
 /
закон тождества/;
/
закон тождества/; -
 и
и  /
транзитивность/;
/
транзитивность/; -
 / сохранение неравенства/;
/ сохранение неравенства/; -
 и
и  / правило знаков/.
/ правило знаков/.
-
 / Теорема Архимеда/.
/ Теорема Архимеда/. -
Теорема Дедекинда о свойстве полноты или непрерывности.
Пусть
![]() ,
где A
и B
–
два непустых непересекающихся множества
таких, что
,
где A
и B
–
два непустых непересекающихся множества
таких, что ![]() (рис.3). Тогда существует
с
такое, что
(рис.3). Тогда существует
с
такое, что ![]() .
.
A B c




Рис.3
О множествах A и B говорят, что они образуют дедекиндово сечение, а о числе с, что оно производит сечение. Это число принадлежит либо A, либо B. В первом случае с в A наибольшее (при этом в B наименьшего числа нет), а во втором случае с в B наименьшее (при этом в A нет наибольшего числа). Единственность очевидна.
Заметим, что множество рациональных
чисел обладает свойствами I – V, но
свойством полноты не обладает.
Действительно, пусть, например, B-множество
положительных рациональных чисел,
квадрат которых больше, чем 2, а A-
остальные рациональные числа. Тогда B
и A, как нетрудно
видеть, образуют дедекиндово сечение
множества рациональных чисел. Но числа
с, производившего сечение, среди
рациональных чисел нет, так как для
этого числа должно быть ![]() .
Следовательно, свойство полноты является
результатом введения иррациональных
чисел. Существуют и другие формулировки
свойства полноты
.
Следовательно, свойство полноты является
результатом введения иррациональных
чисел. Существуют и другие формулировки
свойства полноты ![]() ,
эквивалентные теореме Дедекинда. Они
будут рассмотрены ниже.
,
эквивалентные теореме Дедекинда. Они
будут рассмотрены ниже.
Лекция 3
