
- •Дисциплина «Математический анализ»
- •Раздел I. Введение в анализ
- •§1 Понятие множества. Теоретико-множественные отношения и операции. Декартово произведение.
- •Способы задания множеств
- •Теоретико-множественные отношения
- •Подмножества
- •Теоретико-множественные операции
- •§2 Множество действительных чисел.
- •§3. Изображение действительных чисел на прямой.
- •§4. Основные свойства множества действительных чисел.
- •§5. Модуль действительного числа.
- •Модуль действительного числа обладает свойствами:
- •§6. Числовые множества.
- •§7. Функции и их общие свойства.
- •§8. Действительная функция действительной переменной.
- •§9. Некоторые типы поведения действительных функций действительной переменной. Функции монотонные и кусочно-монотонные.
- •Функции четные и нечетные.
- •Периодические функции.
- •Функции ограниченные и неограниченные.
- •§10. Обратная функция.
- •§11. Числовые последовательности..
- •§12. Принцип вложенных отрезков.
- •§13. Бесконечные десятичные дроби.
- •§14. Предельная точка множества. Теорема Больцано-Вейерштрасса.
- •§15. Понятие предела числовой последовательности.
- •§16. Основные теоремы о пределах последовательностей.
- •§17. Предел монотонной последовательности. Число «e».
- •§18. Критерий Коши.
- •§19. Верхний и нижний пределы.
- •§20. Понятие предела функции.
- •§21. Основные теоремы о пределах функции в точке
- •§22. Предел функции по множеству. Предел на бесконечности.
- •§23. Первый замечательный предел.
- •§24. Второй замечательный предел.
- •§25. Бесконечно малые функции и их сравнения
- •§26 Бесконечно большие функции
§14. Предельная точка множества. Теорема Больцано-Вейерштрасса.
Пусть E – множество,
расположенное на числовой оси, и точка
![]() .
Любой интервал, содержащий точку
.
Любой интервал, содержащий точку ![]() ,
будем называть окрестностью точки
,
будем называть окрестностью точки ![]() .
.
Интервал ![]() ,
где
,
где ![]() ,
будем называть
,
будем называть ![]() - окрестностью точки
- окрестностью точки ![]() и символически обозначать
и символически обозначать ![]()
Если ![]() ,
то это равносильно неравенству
,
то это равносильно неравенству ![]() .
.
Определение. Точка ![]() называется предельной точкой множества
E, если любая ее окрестность
содержит хотя бы одну точку множества
E, отличную от точки
называется предельной точкой множества
E, если любая ее окрестность
содержит хотя бы одну точку множества
E, отличную от точки ![]() .
.
Заметим, что сама точка ![]() может принадлежать, а может и не
принадлежать множеству E.
может принадлежать, а может и не
принадлежать множеству E.
Если точка ![]() ,
но не является предельной, то она
называется изолированной. Иначе говоря,
точка
,
но не является предельной, то она
называется изолированной. Иначе говоря,
точка ![]() называется изолированной точкой этого
множества, если существует окрестность
точки
называется изолированной точкой этого
множества, если существует окрестность
точки ![]() ,
не содержащая точек множества E,
отличных от
,
не содержащая точек множества E,
отличных от ![]() .
.
Теорема 1. Если ![]() предельная
точка множества E, то любая
ее окрестность содержит бесконечное
множество точек E.
предельная
точка множества E, то любая
ее окрестность содержит бесконечное
множество точек E.
Доказательство: Предположим
противное. Пусть ![]() – предельная точка, а некоторая ее
окрестность содержит конечное множество
точек E, отличных от
– предельная точка, а некоторая ее
окрестность содержит конечное множество
точек E, отличных от ![]() .
Обозначим их
.
Обозначим их ![]() . Пусть
. Пусть
 . Тогда
. Тогда ![]() -
окрестность точки
-
окрестность точки ![]() не
будет содержать ни одной точки множества
E, отличной от
не
будет содержать ни одной точки множества
E, отличной от ![]() и, следовательно, точка
и, следовательно, точка ![]() не будет предельной.
не будет предельной.
В определении предельной точки
требовалось, чтобы в любой ее окрестности
нашлась хотя бы одна точка множества
E, отличная от точки ![]() .
.
Из этого требования вытекает, что в действительности в любой окрестности предельной точки будет бесконечно много точек множества E. Отсюда следует, что конечные точечные множества предельных точек не имеют.
Приведем примеры предельных и изолированных точек.
-
Пусть
 , где
, где  (рис.15).
(рис.15).
![]()











Рис. 15
Множество E имеет две
предельные точки ![]() .
Обе они не принадлежат E.
Точки множества E «сгущаются»
у точек 1 и -1 (поэтому предельные точки
множества E часто называют
точками сгущения множества E).
Точка 0 (как и все точки E)
– изолированная точка. Заметим, что все
остальные точки множества E
, будут изолированными.
.
Обе они не принадлежат E.
Точки множества E «сгущаются»
у точек 1 и -1 (поэтому предельные точки
множества E часто называют
точками сгущения множества E).
Точка 0 (как и все точки E)
– изолированная точка. Заметим, что все
остальные точки множества E
, будут изолированными.
В рассмотренном примере точка ![]() является нижней гранью (она не принадлежит
E, но является для E
предельной), а верхней гранью является
точка
является нижней гранью (она не принадлежит
E, но является для E
предельной), а верхней гранью является
точка ![]() ,
которая принадлежит E, но
не является для E предельной.
,
которая принадлежит E, но
не является для E предельной.
Справедлива следующая теорема.
Теорема 2. Если верхняя (нижняя) грань не принадлежит множеству, то она является для этого множества предельной точкой.
Для доказательства этой теоремы достаточно сопоставить определения верхней (нижней) грани и предельной точки.
Рассмотрим другие примеры предельных и изолированных точек.
-
Пусть
 ,
где
,
где  .
Точка
.
Точка  является предельной точкой множества
E.
Действительно, любая окрестность
является предельной точкой множества
E.
Действительно, любая окрестность  содержит хотя бы одну точку множества
E.
Такой точкой будет точка
содержит хотя бы одну точку множества
E.
Такой точкой будет точка  ,
если
,
если  ,
и достаточно взять
,
и достаточно взять  Все точки множества E
являются изолированными.
Все точки множества E
являются изолированными. -
Пусть
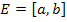 .
Здесь всякая точка
.
Здесь всякая точка  является предельной. В самом деле, любая
окрестность точки
является предельной. В самом деле, любая
окрестность точки  содержит точки отрезка. Кстати, здесь
все предельные точки принадлежат
множеству E.
содержит точки отрезка. Кстати, здесь
все предельные точки принадлежат
множеству E.
-
Пусть
 Здесь
все точки E
будут предельными, но кроме того, будут
предельными и точки a,
b.
В отличие от других предельных точек,
они не принадлежат множеству E.
Здесь
все точки E
будут предельными, но кроме того, будут
предельными и точки a,
b.
В отличие от других предельных точек,
они не принадлежат множеству E. -
Пусть
 .
Это множество предельных точек не
имеет. Все его точки изолированные.
.
Это множество предельных точек не
имеет. Все его точки изолированные.
Множество
предельных точек множества E
принято обозначать через ![]() .
.
Точки множества E и его
предельные точки принято называть
точками прикосновения для множества
E, а их совокупность
обозначают через ![]() Очевидно,
Очевидно, ![]()
Последний пример показывает, что не всегда бесконечное множество имеет предельные точки. Следующая теорема устанавливает класс бесконечных множеств, имеющих предельные точки.
Теорема 3. (Больцано-Вейерштрасса). Всякое бесконечное ограниченное множество имеет хотя бы одну предельную точку.
Доказательство. Так как E
ограничено, то можно указать отрезок
![]() ,
содержащий множество E.
Положим
,
содержащий множество E.
Положим ![]() .
Тогда хотя бы один из отрезков
.
Тогда хотя бы один из отрезков ![]() содержит бесконечное множество точек
E. Обозначим его через
содержит бесконечное множество точек
E. Обозначим его через ![]() Отрезок
Отрезок ![]() вновь разделим пополам и обозначим
через
вновь разделим пополам и обозначим
через ![]() ту половину, которая содержит бесконечное
множество точек E. Продолжая
процесс, мы получим бесконечную
последовательность вложенных отрезков
ту половину, которая содержит бесконечное
множество точек E. Продолжая
процесс, мы получим бесконечную
последовательность вложенных отрезков
![]() ,
каждый из которых содержит бесконечное
множество точек E. Так как
длина отрезка
,
каждый из которых содержит бесконечное
множество точек E. Так как
длина отрезка ![]() равна
равна ![]() ,
то для любого положительного числа
,
то для любого положительного числа
![]() найдется
найдется ![]() ,
что для всех
,
что для всех
![]() .
.
Следовательно, по теореме Кантора
существует единственная точка ![]() ,
общая точка для всех отрезков
,
общая точка для всех отрезков ![]() .
.
Докажем теперь, что точка ![]() предельная точка множества E.
предельная точка множества E.
Рассмотрим произвольный интервал ![]() ,
содержащий точку
,
содержащий точку ![]() При достаточно большом
При достаточно большом ![]() .Так
как отрезок
.Так
как отрезок ![]() содержит бесконечное множество точек
E, то и интервал
содержит бесконечное множество точек
E, то и интервал ![]() содержит бесконечное множество точек
E. Значит, точка
содержит бесконечное множество точек
E. Значит, точка ![]() - предельная для множества E.
- предельная для множества E.
Итак, отметим:
-
Множество E может иметь не одну предельную точку (пример 3).
-
Предельная точка может и не принадлежать множеству E (пример 2).
-
Оба условия теоремы существенны. Пример 5 показывает, что существуют неограниченные бесконечные множества, не имеющие предельных точек, а конечные множества, как было показано, предельных точек не имеют.
