Содержание

Структурный анализ зубчато-рычажного механизма…………………………………………………………………3

Кинематическое исследование механизма методом планов в рабочем положении…….6

Построение плана скоростей рабочего положения. ……………………...............................................8

Построение плана ускорений………………………………………………………………………………………………………9

Силовой расчет механизма…………………………………………………………………………………………………………………….…11

Определение сил, действующих на звенья механизма…………………………………………………12

Силовой расчет группы 3-4 [В₂₃-В₃₄-П₄₀]…………………………………………………………………………….13

Силовой расчет группы 2-2’[ВП₁₂-В₀₂]…………………………………………………………………………………..14 Силовой расчет начального механизма В₀₁………………………………………………………………………..16

Рычаг Жуковского…….…………………………………………………………………………………………………………………………………17

Расчет КПД механизма. …………………………………………………………………………………………………………………………..18

Балансировка ротора ……………………………………………………………………………………………………………………………….19

Кинематический анализ зубчатых механизмов.………………………………………….…………………………………23

Литература……………………………………………………………………………………………………………………………………………………25

Структурный анализ зубчато-рычажного механизма

Цель структурного анализа – выявить строение (структуру) механизма.

При этом необходимо:

1. определить число звеньев механизма и назвать каждое из них;

2. определить число кинематических пар и дать характеристику (соединения каких звеньев, вид (вращательная, поступательная), характер соприкосновения звеньев (низшая или высшая кинематическая пара), число степеней свободы(класс));

3. выявить структурные группы (группы Ассура), входящие в состав механизма; привести схемы групп, назвать их, определить класс группы, написать формулу строения;

4. определить степень подвижности механизма(по формуле П.Л.Чебышева);

5. привести формулу строения механизма(в общем и развернутом виде).

Структурный анализ механизма

Подвижные звенья		Кинематические пары
Схема	Название	Схема	Вид	Степ. Подв.	Символ	Класс пары	Высш.. или Низш.
	Шестер-ня-ведущее звено		Вращ.	1	В01	Р5	Низш.
			Вращ.-поступ.	2	ВП12	Р4	Высш.
	Зубчатое колесо-кривошип
			Вращ.	1	В02	Р5	Низш.
	Шатун		Вращ..	1	В2’3	Р5	Низш.
			Вращ.	1	В34	Р5	Низш.
	Ползун
			Поступ..	1	П40	Р5	Низш.

Число подвижных звеньев n=4

Число кинематических пар: всего-6, из них пятого класса Р₅ =5, четвертого класса Р₄=1

Степень подвижности механизма: W=3·n-2·P₅ -P₄=12-10-1=1

Примечание: пассивных звеньев и кинематических пар механизм не содержит

0. Структурный состав механизма.

Начальный механизм и структурные группы (группы Ассура)
Схема	Название, класс, порядок, вид.	Число звеньев	Число кинематических пар		Формула строения
			Всего	Поводковых
	Начальный вращательный механизм 1 класса	1	1	-	В01
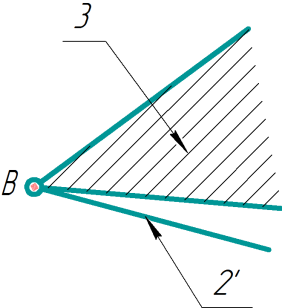
	Однозвеньевая двухповодковая группа Ассура с высшей кинематической парой	1	2	2	ВП12-В02
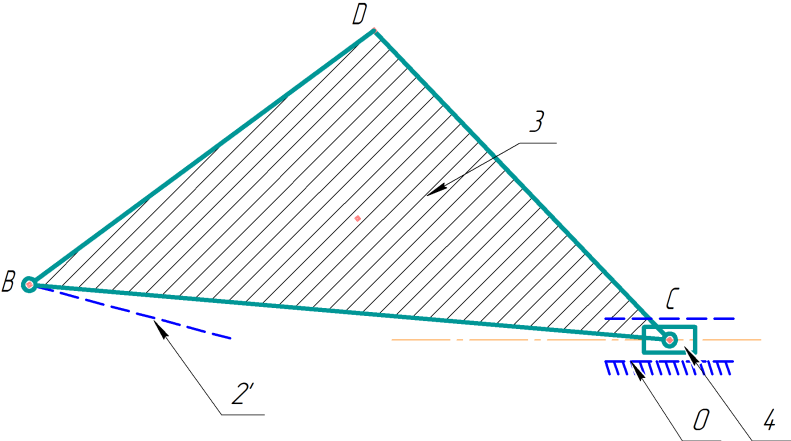
	Двухзвеньевая двухповодковая группа Ассура 2 класса 2 порядка	2	3	2	В23-В34-П40
Начальный механизм -1. Cтруктурных групп(групп Ассура) -2, соединение групп- последовательное, механизм второго класса. Формула строения: В01 - [ВП12-В02 ] - [В23-В34-П40 ]

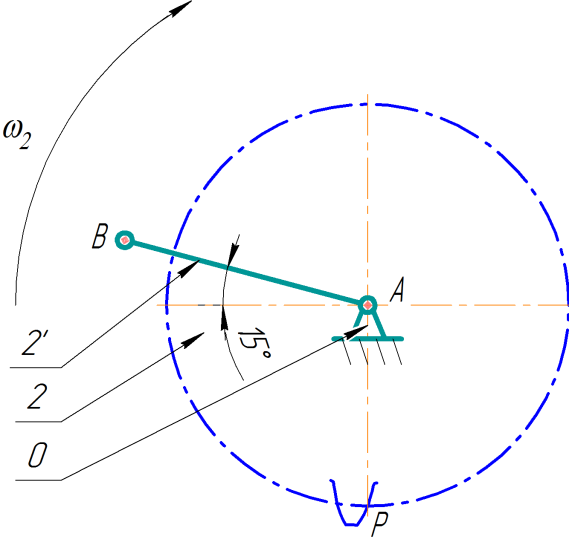
Кинематическое исследование механизма методом планов в рабочем положении.

Задача кинематического исследования механизма состоит в определение:

- численных значений линейных скоростей всех характерных точек механизма (кинематических пар, центров тяжести) и угловых скоростей всех звеньев для рассматриваемых положений, для чего построить планы скоростей для рабочего положения;

- численных значений линейных ускорений всех характерных точек механизма и угловых ускорений всех звеньев для данных положений, для чего построить планы ускорений для того же положения;

- траекторий некоторых точек звеньев.

Построение плана скоростей рабочего положения.

d₁ = m∙z₁ = 2 ∙18 = 36 мм = 0,036 м;

d₂ = m∙z₂ = 2 ∙ 20 = 40 мм = 0,04 м;

V_A =V_F = 0

Угловая скорость колеса 1:

ω₁ == с ^-1;

Частота вращения колеса 2:

n₂ = n₁ ∙ z₁/z₂ = об./мин;

Угловая скорость колеса 2:

ω₂ == с ^-1;

Определим линейную скорость точки В звена 2

V_В = ω₂∙ l_AB = м/с;

Строим точку b на плане скоростей. Для этого задаем масштаб плана скоростей:

μ_v= 0,005 (м/с)/мм;

Находим длину вектора скорости точки B на плане скоростей:

P_vb = V_В / μ_v = 0,4712/0,005 = 94,2478 мм;

На плане скоростей из произвольной точки P_v (полюса) проводим линию, перпендикулярную прямой АВ на плане механизма и откладываем отрезок равный P_vb .

Находим скорость точки С . Для этого решаем систему двух векторных уравнений:

;

где – V_В скорость точки В (найдена),

V_C – направление вектора скорости нам известно. Вектор направлен вдоль горизонтальной оси.

V_CB CB –скорость точки С при вращении звена ВDС вокруг оси шарнира В (направлена перпендикулярно линии ВС)

Построение точки с на плане скоростей ведем в следующей последовательности:

Из точки b проводим направление скорости V_СВ – линию перпендикулярную линии ВС.

Из полюса проводим вектор V_C до пересечения с вектором V_CB. Точка пересечения векторов и есть точка с.

Скорость V_С точки С равна:

V_С = P_vc ∙ μ_v = 16,5101 ∙ 0,005 = 0,0826 м/с;

Скорость точки D найдем по правилу подобия:

Строим треугольник bdc подобный треугольнику BDC

мм;

мм;

V_D = P_vd ∙ μ_v = 73,7514 ∙ 0,005 = 0,3688 м/с;

Угловая скорость 3-его звена:

ω₃ = V_BC / l_BC = μ_v∙ bc/ l_BC = с ^-1;

ω2, с -1	VA =VF, м/с	VВ, м/с	VС, м/с	VD, м/с	ω3, м/с
20,944	0	0,4712	0,0826	0,3688	6,0918