3.1.1.2. Квантование

После дискретизации сигналов по времени осуществляется квантование выборочных значений, состоящее в преобразовании непрерывных по амплитуде значений сигнала в моменты отсчета в дискретное с последующим кодированием, т.е. представлением полученной квантованной последовательности цифровым кодом в соответствии с принятой системой счисления (обычно двоичной).

Квантование по уровню может быть равномерным и неравномерным. При равномерном квантовании весь диапазон изменения сигнала разбивается на одинаковых частей - интервалов квантования. Под шагом (интервалом) квантования понимается разность , где - соседние уровни квантования.

При неравномерном квантовании шаг квантования непостоянен. На практике преимущественное применение получило равномерное квантование в связи с простотой его технической реализации.

Шкала значений сигнала может быть разбита на отдельные участки различным образом: с привязкой уровней квантования к точке ; к границам диапазона изменения сигнала и т.д. (рис.3.12).

Рис.3.12. Способы квантования шкалы параметра

Для случая, приведенного на рис.3.12а, первый уровень квантования совмещен с началом шкалы , а - й уровень совпадает с концом шкалы . Для этого случая шаг равномерного квантования

(3.13)

На рис.3.12б начальный уровень квантования отстоит от начала шкалы на величину . Как видно, для рассмотренных вариантов положение уровня является фиксированным.

Обычно на практике применяют два способа отнесения значений сигнала к соответствующему уровню квантования /5,9/. При первом из них мгновенные значения функции заменяются меньшим дискретным значением, рис.3.13а. При втором - ближайшим меньшим или ближайшим большим дискретным значением в зависимости от того, какое из этих значений ближе к мгновенному значению функции. В этом случае переход ступенчатой функции с одной ступени на другую происходит в те моменты, когда первоначальная непрерывная функция пересекает середину между соответствующими соседними дискретными уровнями, рис.3.13б.

Рис.3.13. Квантование непрерывных процессов: а) с усечением, б) с округлением

Устройство для квантования сигналов по уровню, называемое квантователем (квантизатором), представляет собой нелинейный элемент с амплитудной характеристикой, приведенной на рис.3.14а, при отождествлении сигнала с ближайшим меньшим уровнем квантования или, приведенной на рис.3.14б, в случае отождествления сигнала с ближайшим большим или меньшим уровнем.

Рис.3.14. Характеристика равномерных квантователей:

а) - с усечением; б) – с округлением

Квантование по уровню сопровождается методической погрешностью, которая связана с заменой истинного значения сигнала уровнем квантования . Эта погрешность получила название погрешности квантования или шума квантования. Абсолютное значение этой погрешности в каждый момент времени определяется разностью между квантованным значением и действительным мгновенным значением функции .

(3.14)

На рис.3.15а и 3.15б показан характер изменения абсолютного значения погрешности квантования для способов квантования, представленных на рис.3.14а и 3.14б, соответственно.

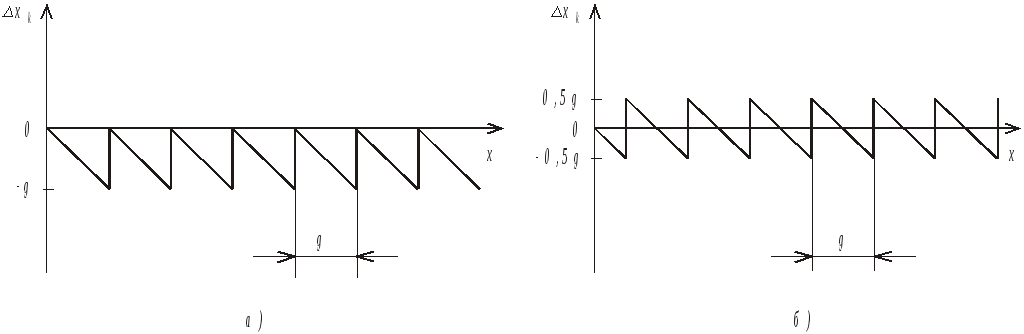
Рис.3.15. К определению погрешности квантования:

а) с усечением, б) - с округлением.

Как видно, в первом случае абсолютная погрешность квантования будет всегда отрицательной в пределах . Во втором - изменяется от минус до плюс . Максимальная погрешность, как легко видеть из приведенных рисунков, для первого способа квантования равна

(3.15)

а для второго способа она не превышает , т.е. способ квантования по уровню, отождествляющий сигнал с ближайшим меньшим или большим уровнем квантования, приводит к снижению максимальной погрешности квантования в два раза.

Закон распределения этой погрешности зависит от закона распределения . Можно показать, что при идеальном преобразовании с достаточно большим числом уровней квантования погрешность квантования подчиняется равномерному закону распределения, который для первого случая имеет следующий вид:

(3.16)