3.1.1. Дискретизация и квантование

3.1.1.1. Дискретизация.

В основу дискретизации положена принципиальная возможность представления непрерывных сигналов в виде взвешенных сумм:

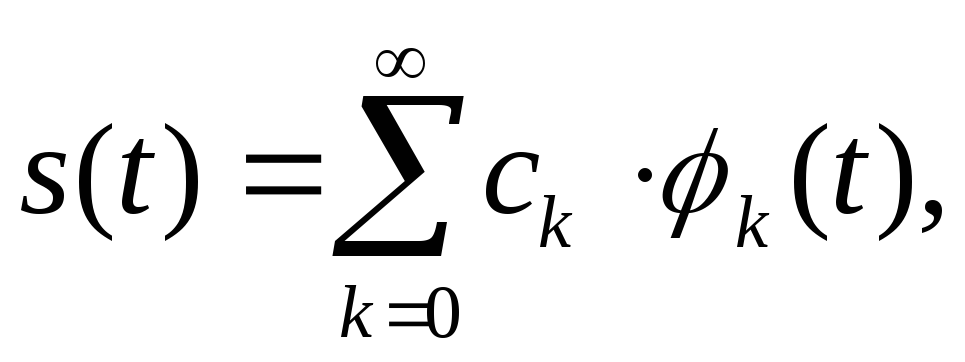(3.1)

где - некоторые коэффициенты или отсчеты, характеризующие исходный сигнал в дискретные моменты времени,

- набор элементарных функций, с помощью которых происходит восстановление сигнала по его отсчетам.

Очевидно, что по дискретным значениям исходную функцию можно восстановить с некоторой погрешностью. Часто функцию, полученную в результате восстановления (интерполяции) по значениям , называют воспроизводящей и обозначают каким-либо другим, отличным от исходного сигнала , символом, например /4/ .

Понятно, что при обработке сигналов дискретизация по времени должна производиться таким образом, чтобы по отсчетным значениям можно было бы получить воспроизводящую функцию , которая с заданной точностью отображает исходную функцию .

Как уже отмечалось, при дискретизации приходится решать вопрос о том, как часто следует брать отсчеты функции, т.е. каким должен быть шаг дискретизации

При малом количество отсчетов преобразуемого сигнала на интервале обработки будет большим и точность воспроизведения - высокой. Однако при отсчетах, взятых в слишком близко расположенных точках, будут получаться коррелированные данные, число которых будет избыточно велико, что неизбежно вызовет увеличение как объема, так и стоимости расчетов. С другой стороны, при больших количество отсчетов уменьшится, но при этом, как правило, снижается точность восстановления и, кроме того, при дискретизации реальных сигналов может привести к явлению наложения (маскировки) низко- и высокочастотных составляющих. Оптимальной является такая дискретизация, которая обеспечивает представление исходного сигнала с заданной точностью при минимальном числе выборок, обусловленными необходимостью адекватного представления существенной информации, содержащейся в высокочастотной части спектра сигнала.

Наиболее распространенной является равномерная дискретизация, при которой шаг (интервал) дискретизации остается постоянным:

Величина, обратная интервалу дискретизации, называется частотой дискретизации.

Методы равномерной дискретизации нашли широкое применение вследствие того, что алгоритмы дискретизации и восстановления сигналов, а также соответствующая аппаратура, реализующая их, в этом случае достаточно просты.

Равномерная дискретизация, как известно, основывается на разложении исходного непрерывного сигнала в ряд Котельникова. Это разложение составляет основу теоремы Котельникова (за рубежом ее называют теоремой Шеннона, или просто теоремой отсчетов). Суть теоремы отсчетов состоит в следующем: непрерывная функция времени , не содержащая частот выше , полностью определяется отсчетами мгновенных значений в точках, отстоящих друг от друга на интервал .

В формулировке автора эта теорема звучит так: любую функции , состоящую из частот от до , можно непрерывно передавать с любой точностью при помощи чисел, следующих друг за другом через с.

В этом случае исходный сигнал может быть восстановлен без погрешностей по точным значениям выборок в виде

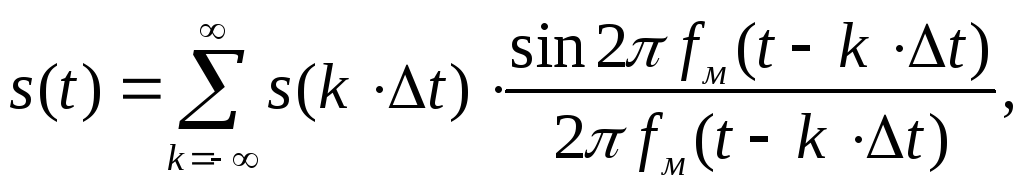(3.2)

где - шаг (интервал) дискретизации.

Из выражения (3.2) видно, что непрерывная функция представляется суммой (бесконечной) произведений, один из сомножителей которых есть выборка функции, а другой - так называемая функция отсчетов

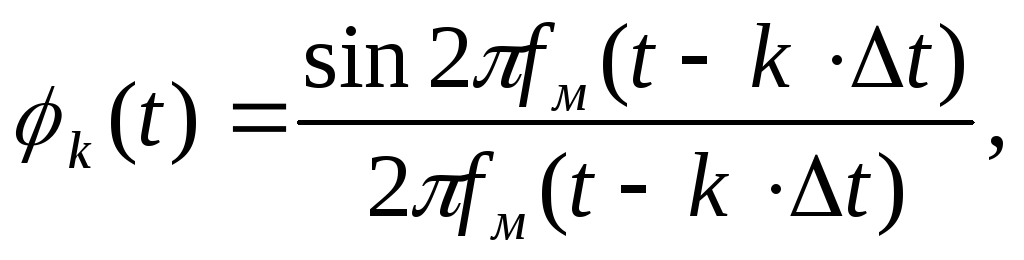(3.3)

график которой приведен на рис.3.4.

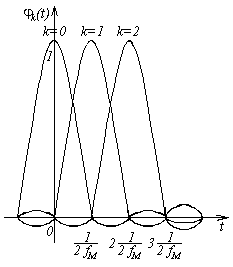
Рис.3.4. Функции отсчетов

Свойства функции отсчетов:

1) в момент времени функция достигает своего наибольшего значения, равного единице;

2) в моменты времени , где - любое целое положительное число, функция обращается в нуль;

3) функции отсчетов ортогональны с весом единица на бесконечном интервале времени;

4) ширина лепестка функций отсчетов на нулевом уровне равна .

Каждое слагаемое ряда (3.2) можно рассматривать как отклик идеального фильтра нижних частот с верхней граничной частотой , когда на вход фильтра поступает - импульс, тождественный выборке временной функции в момент .Следует отметить, что идеальный фильтр физически не реализуем.

При практическом применении теоремы отсчетов возникают некоторые дополнительные погрешности представления. Наиболее существенными из них являются следующие. Теорема отсчетов относится к сигналам с ограниченным спектром. Реальные сигналы, являющиеся носителями информации, имеют ограниченную длительность. Следовательно, точное разложение (3.2) заменяется следующим приближенным:

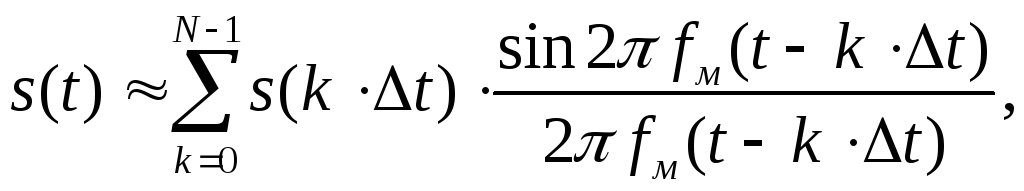(3.4)

Причем, общее число независимых параметров, т.е. значений равно , если учитывать отсчеты на концах интервала обработки . Обычно и полагают равным .

Очевидно, что погрешность представления будет в этом случае тем больше, чем меньше число членов разложения участвует в восстановлении функции .

Другая причина, вызывающая погрешность при представлении реальных сигналов рядом Котельникова, состоит в том, что из-за конечной длительности их частотный спектр не ограничен. Если ограничить реальный спектр сигнала, простирающийся от нуля до бесконечности, некоторым диапазоном частот от нуля до , в котором сосредоточена основная часть энергии, то дисперсия приведенной погрешности будет определяться выражением /5/:

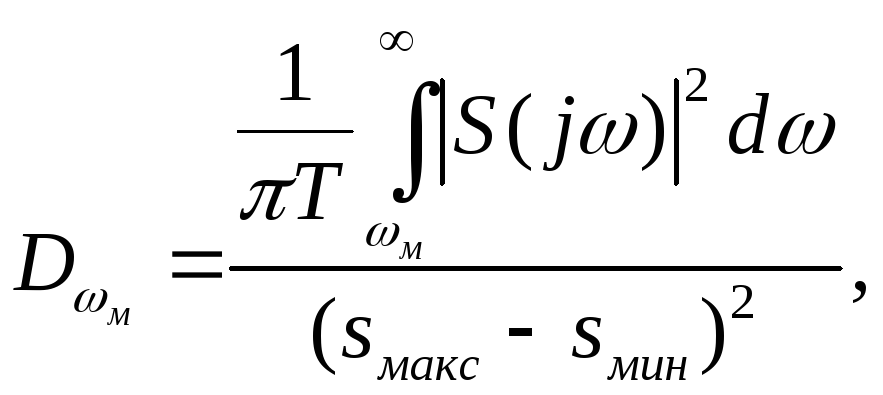(3.5)

где - преобразование Фурье исследуемого сигнала,

Т - длительность функции s(t),

- пиковые значения функции s(t).

Нетрудно заметить, что числитель выражения (3.5) определяет среднюю мощность отсекаемой части частотного спектра функция s(t).

Для удобства расчётов (3.5) можно представить в виде

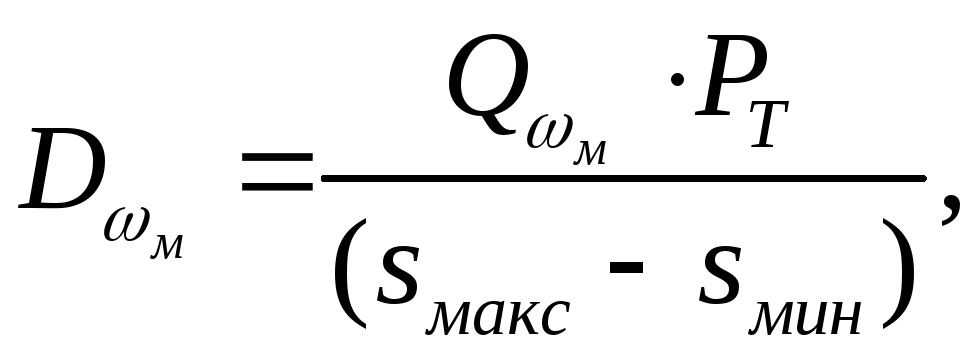(3.6)

где 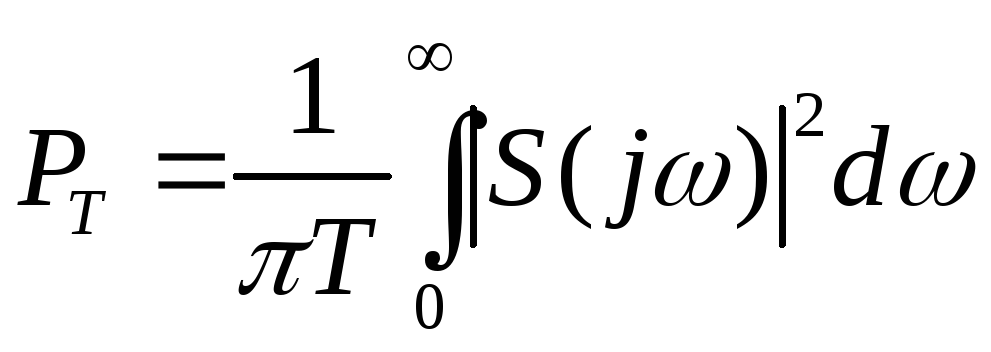- средняя мощность сигнала,

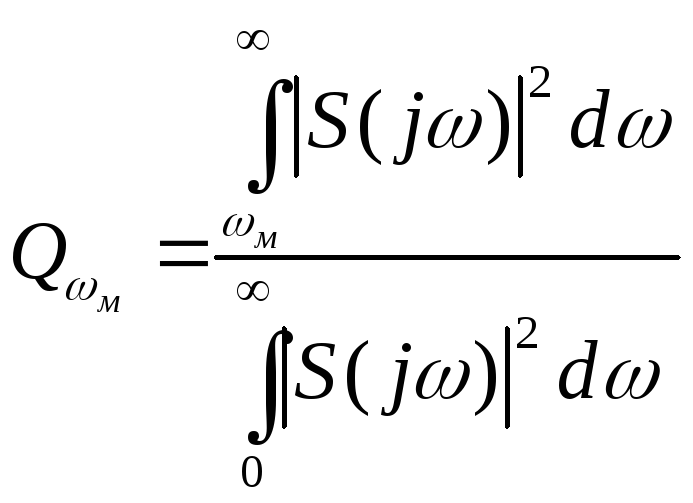- относительная площадь отсекаемого участка энергетического спектра сигнала s(t).

Выражение (3.6) по заданной величине и при известных и спектре функции s(t) позволяет определить частоту , ограничивающую спектр.

Теорема отсчетов может быть обобщена и на случай сигналов, спектр которых начинается не с нулевой частоты.

В идеальном случае процесс дискретизации можно представить как произведение исходного сигнала s(t) на последовательность единичных импульсов (дельта-импульсов):

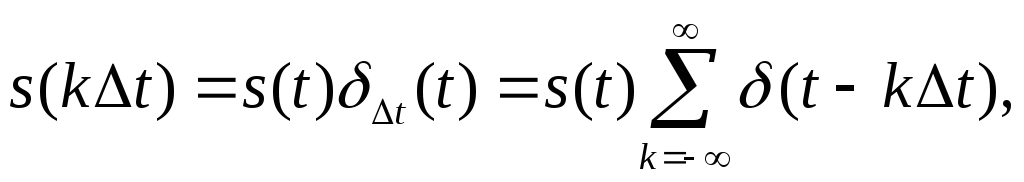(3.7)

где - интервал дискретизации,

(t) - дельта-функция Дирака.

Найдем преобразование Фурье выражения (3.7). На основании теоремы о свертке получим:

(3.8)

где и - преобразование Фурье функций и соответственно,

- условное обозначение операции свертки,

F - оператор преобразования Фурье.

Так как

где - частота дискретизации,

то выражение (3.8) можно представить в виде:

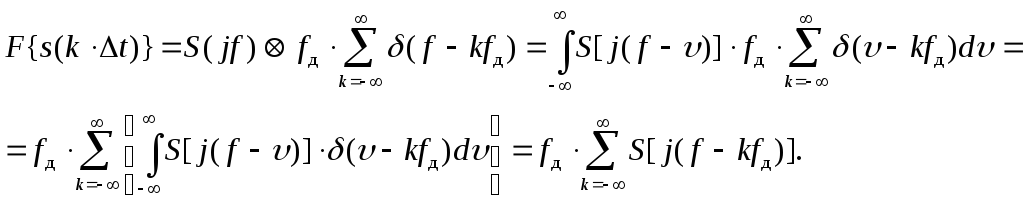
Отсюда видно, что спектр исходного сигнала повторяется по частоте через интервал Гц. Графически это выглядит следующим образом, рис.3.5.

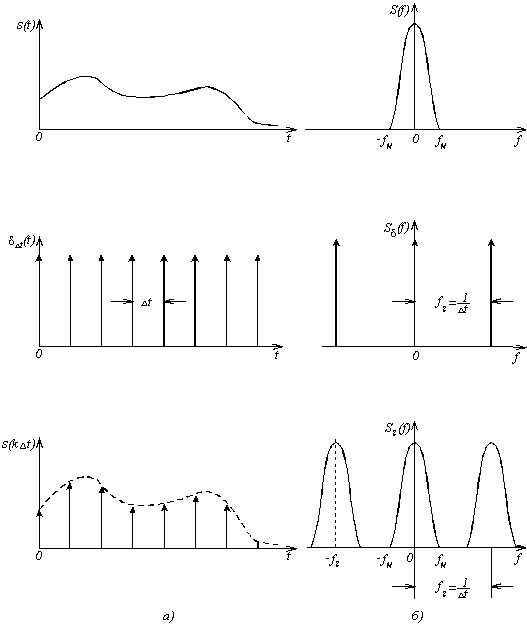
Рис.3.5. Дискретизация сигналов с помощью последовательности единичных импульсов; а) – представление во временной области; б) – представление в частотной области.

Как видно, спектр исходного сигнала повторяется периодически без взаимного перекрытия, если или, что тоже самое

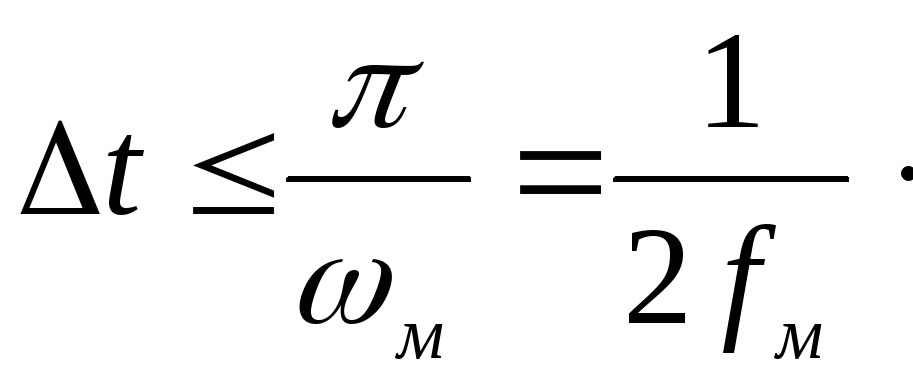
Следующий рисунок 3.6 иллюстрирует различные соотношения между частотой дискретизации и максимальной частотной составляющей в спектре преобразуемого сигнала.

Рис.3.6. Иллюстрация соотношения между частотой дискретизации и максимальной частотой в спектре сигнала

Легко заметить из первых двух рисунков, что форма спектра сохраняется в диапазоне частот выше удвоенной максимальной частоты в спектре исходного сигнала, т.е. при выборе частоты дискретизации (в том случае, когда спектр преобразуемого сигнала резко ограничен частотой ). При неправильном выборе частоты дискретизации составляющие спектра, превышающие частоту нельзя будет отличить от составляющих, лежащих в интервале частот от 0 до , что приводит к возникновению эффекта, известного как наложение спектров (aliasing).

В самом деле, нетрудно показать, что

если выборка осуществляется в моменты времени . В этом случае для любой частоты из диапазона 0 - имеется набор частот, замаскированных под

Например, если =200 Гц, то составляющие с частотой 30 Гц будут неотделимы от составляющих с частотами 170, 230, 370, 430 и т.д. Эти составляющие будут неотделимы в том смысле, что в точках дискретизации они имеют одинаковые значения, рис.3.7.

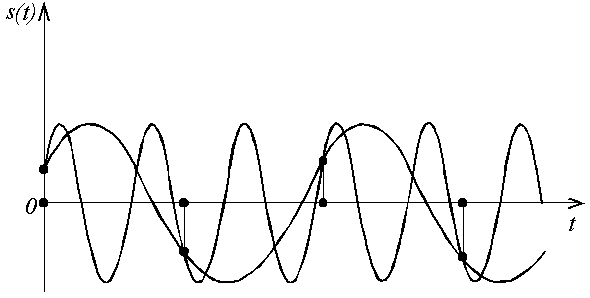
Рис.3.7. Частотные искажения (эффект наложения), связанные с дискретизацией

Влияние дискретизации будет проявляться в том, что энергия составляющих с частотами выше будет отражена в главный диапазон энергетического спектра симметрично относительно , рис.3.8.

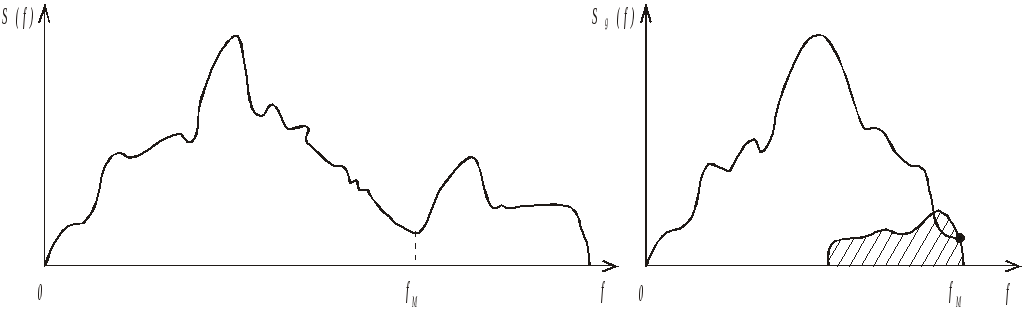
Рис.3.8. Влияние дискретизации на энергетический спектр преобразуемых сигналов: а) - энергетический спектр непрерывного сигнала; б) - энергетический спектр после дискретизации

Это явление известно из кино и телевидения. По мере того как колеса телеги вращаются все быстрее и быстрее, нам кажется, что они замедляют свое движение и затем останавливаются. Если частота вращения продолжает увеличиваться, то будет казаться, что колеса вращаются назад, останавливаются, вращаются вперед и так последовательно несколько раз. Очевидно, что эти эффекты связаны с дискретизацией изображения кинокамерой.

Таким образом, явление наложения или маскировки частот, несвойственное аналоговым методам обработки, является источником специфической погрешности, которую необходимо учитывать при практическом применении цифровых методов обработки сигналов.

В заключение уточним некоторые термины теории дискретизации, встречающиеся в литературе. Для этого обратимся к рисунку 3.9.

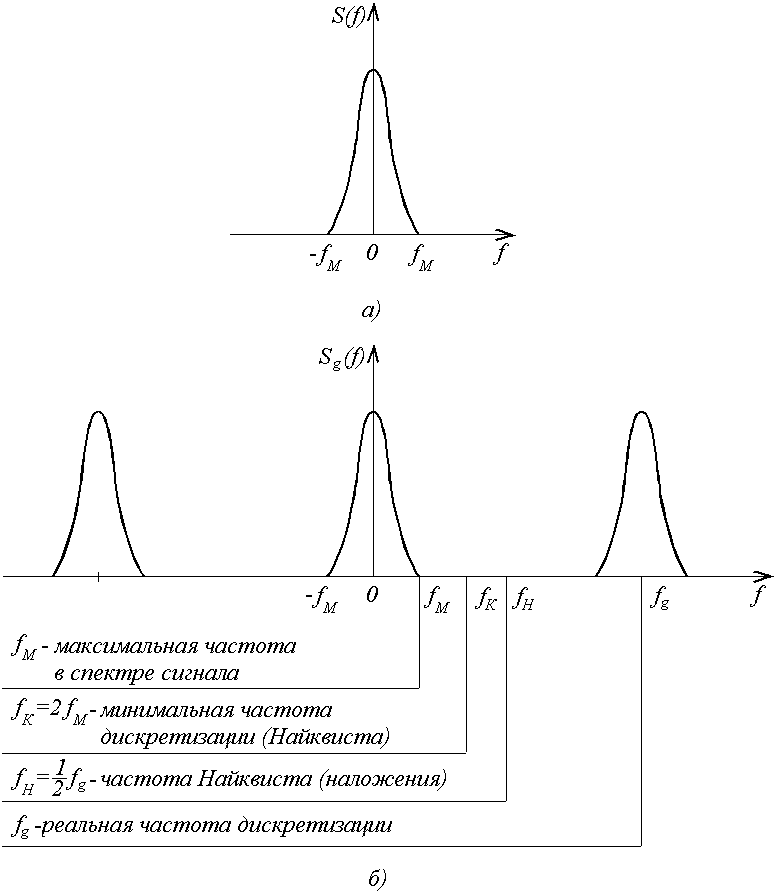
Рис.3.9. Наглядное представление некоторых терминов теории дискретизации: а) - спектр исходного сигнала; б) - спектр сигнала после дискретизации

Наивысшая частота , присутствующая в спектре сигнала, иногда называется частотой Котельникова. Частота является наименьшей частотой, при которой можно дискретизировать сигнал, а затем восстановить его по дискретным отсчетам. Интервал – интервал Котельникова (Найквиста). Частота - это частота дискретизации, выбранная в конкретной (реальной) системе обработки. Величина, обратная реальной частоте дискретизации, называется интервалом (шагом) дискретизации. Частотой Найквиста (наложения) обычно называют половину реальной частоты дискретизации.