Лабораторная работа №1 исследование способов формирования нечетких множеств и операции над ними

Цель работы: Изучить методы построения нечетких множеств с использованием различных типов функций принадлежности. Ознакомиться с наиболее распространенными логическими операциями над нечеткими множествами.

Теоретическая часть

Теория нечетких множеств и основанная на ней логика позволяют описывать неточные категории, представления и знания, оперировать ими и делать соответствующие заключения и выводы. Наличие таких возможностей для формирования моделей различных объектов, процессов и явлений на качестсвенном, понятийном уровне определяет интерес к организации интеллектуального управления и обработки информации на основе применения методов нечеткой логики.

Формализация понятия нечеткого множества основана на использовании так называемой функции принадлежности (ФП), которая в свою очередь является обобщением характеристической функции, определяющей обычное (четкое) множество.

Характеристическая функция , определяющая множество в полном пространстве , представляет собой отображение, для которого есть область определения, а (двузначное множество из 0 и 1) есть область значений:

или

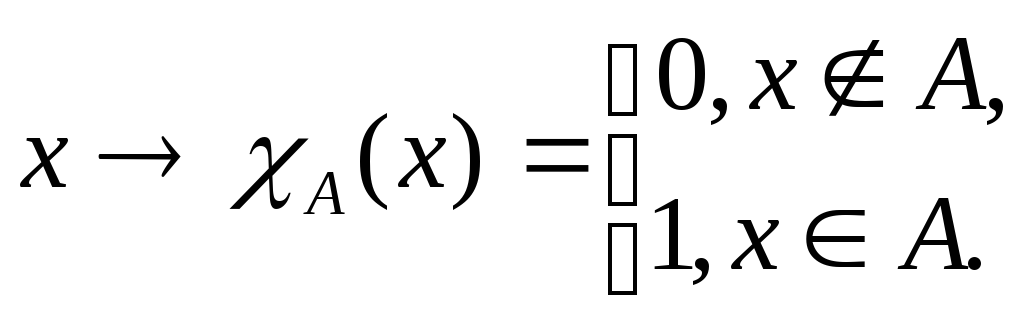
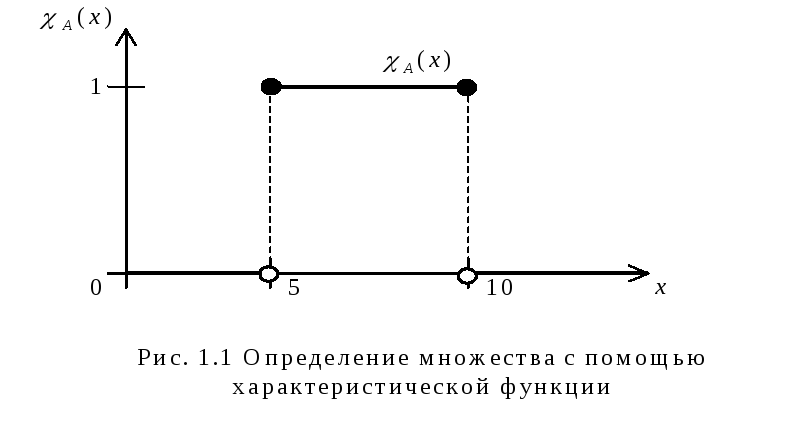
При этом , если элемент удовлетворяет свойствам , и 0, если не удовлетворяет. Графическое представление характеристической функции показано на рис. 1.1 ( - множество действительных чисел от 5 до 10 включительно).

Нечеткое множество является расширением классического (четкого) множества. ФП, описывающая нечеткое множество, принимает свои значения в интервале [0,1] и отражает субъективную оценку степени принадлежности отдельных элементов базовой шкалы соответствующему нечеткому множеству:

где - определяемое нечеткое множество; - исходная базовая шкала (область определения); - функция принадлежности.

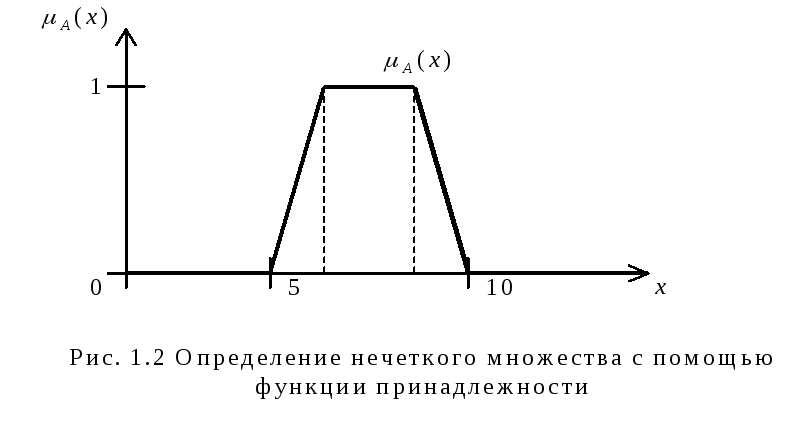
Нечеткое множество может задаваться и непосредственно в виде ФП, являющейся его исчерпывающей характеристикой (рис. 1.2):

Важнейшими логическими операциями из числа разрешенных над нечеткими множествами являются пересечение, объединение и дополнение (отрицание). Эти операции соответственно записываются следующим образом:

(1)

где

Логические операторы

Конъюнктивные и дизъюнктивные операторы ()

Конъюнктивные операторы	Дизъюнктивные операторы
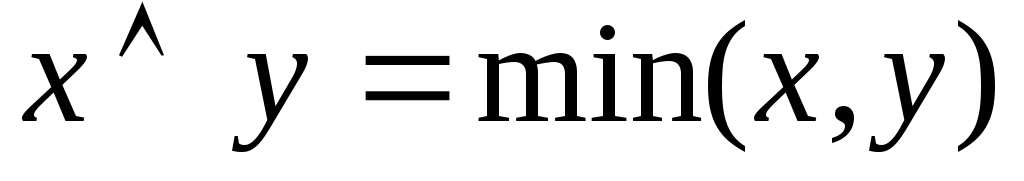
Оператор минимума	Оператор максимума
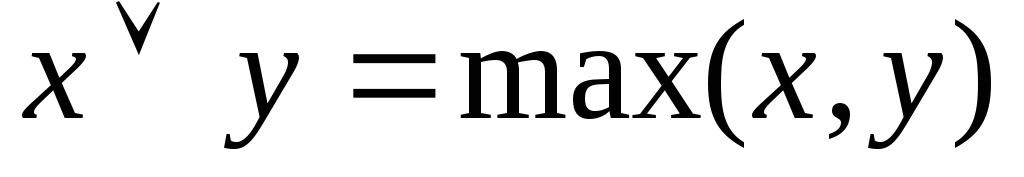
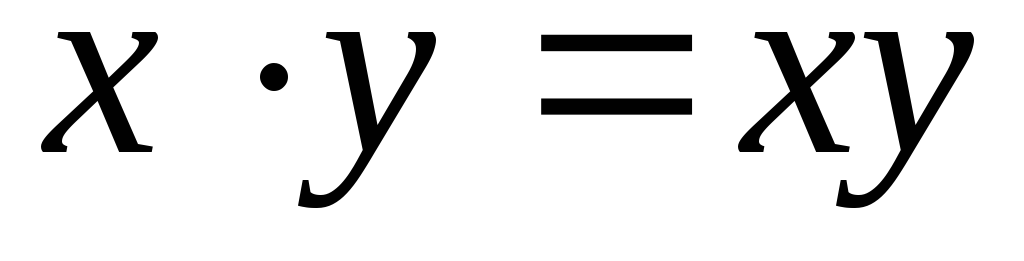
Алгебраическое произведение	Алгебраическая сумма

Практическая часть

1. Используемые типы функций принадлежности в matlab

Инструментарий нечеткой логики (ИНЛ) в составе пакета MATLAB содержит 11 встроенных типов функций принадлежности, формируемых на основе кусочно-линейных функций, функции распределения Гаусса, сигмоидной кривой и квадратических и кубических полиномиальных кривых.

К наиболее простым ФП можно отнести треугольную и трапециевидную ФП. Наименование треугольной ФП - trimf (mf - указывает на принадлежность к ФП (membership function). В параметрическом виде она представляет собой ни что иное, как набор трех точек, образующих треугольник.

Описание функции:

y = trimf(x, [a b c])

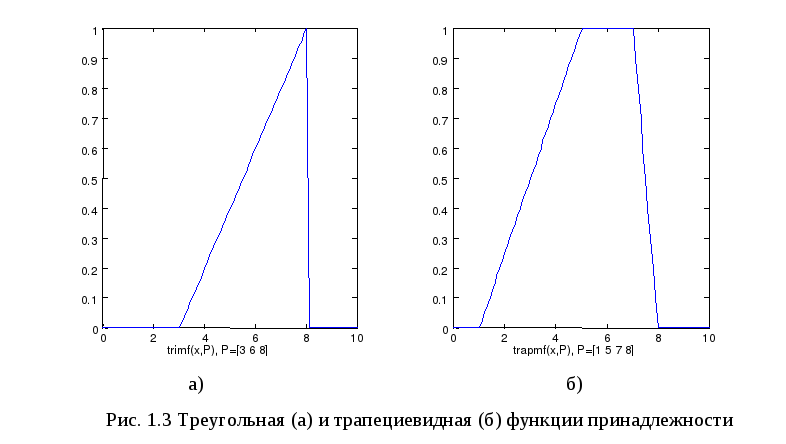
Вектор x определяет базовое множество, на котором определяется ФП. Величины a и c задают основание треугольника, а величина b - его вершину (рис. 1.3, а).

В аналитическом виде треугольная ФП может быть задана следующим образом:

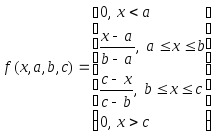
Пример 1.1

x=0:0.1:10; Задается базовое множество

y=trimf(x,[3 6 8]); Определяется треугольная ФП

plot(x,y); Вывод графика функции

xlabel('trimf(x,P), P=[3 6 8]') Подпись графика под осью абсцисс

Трапециевидная ФП, trapmf, отличается от предыдущей функции лишь тем, что имеет верхнее основание.

Описание функции:

y = trаpmf(x, [a b c d]),

где параметры a и d задают нижнее основание, а b и c - верхнее основание трапеции (рис. 1.3, б).

Аналитическая запись трапециевидной функции следующая:

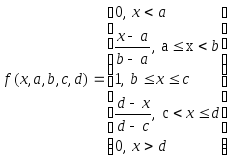
Одним из основных достоинств треугольных и трапециевидных ФП является их простота.

На основе функции распределения Гаусса в MATLAB, используя ИНЛ, есть возможность построения двух ФП: простая ФП Гаусса и двухсторонняя ФП, образованная с помощью двух различных функций распределения Гаусса. Первая из них обозначается - gaussmf, а вторая - gauss2mf.

Описание функции:

y = gaussmf(x, [, c]).

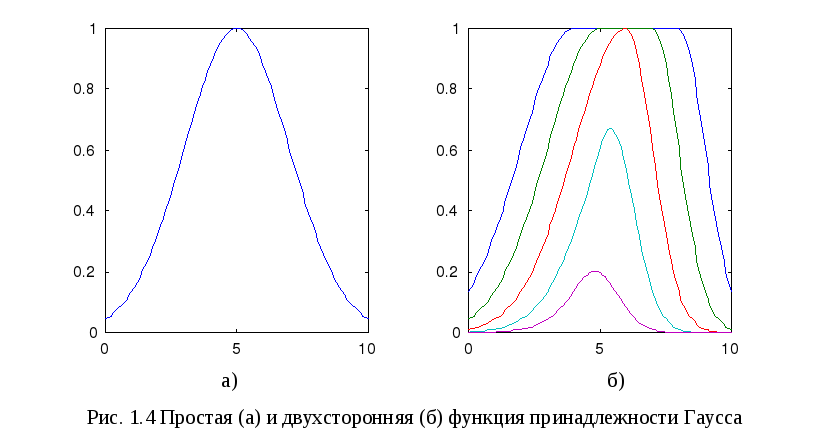
Симметричная функция Гаусса зависит от двух параметров и с (рис. 1.4, а):

.

Пример 1.2

x=0:0.1:10;

y=gaussmf(x,[2 5]);

plot(x,y)

Описание функции:

y = gauss2mf(x, []).

Данная функция является комбинацией двух различных функций распределения Гаусса. Первая функция распределения, определяемая параметрами и задает форму левой стороны, а вторая функция (параметры , ) - правой стороны ФП.

Если <, то в этом случае функция gauss2mf достигает своего максимального значения на уровне 1. Иначе - максимальное значение функции меньше, чем 1 (рис.1.4, б).

Пример 1.3

x = (0:0.1:10)';

y1 = gauss2mf(x, [2 4 1 8]);

y2 = gauss2mf(x, [2 5 1 7]);

y3 = gauss2mf(x, [2 6 1 6]);

y4 = gauss2mf(x, [2 7 1 5]);

y5 = gauss2mf(x, [2 8 1 4]);

plot(x, [y1 y2 y3 y4 y5])

Символ “ ‘ ” в строке определения базового множества x показывает свойство транспонированности.

Следующей функцией, которая позволяет представлять нечеткие субъективные предпочтения, является ФП “обобщенный колокол” и обозначается - gbellmf. Основное ее отличие от двух ранее рассмотренных ФП, основанных на функции распределении Гаусса, заключается в добавлении третьего настраиваемого параметра, что позволяет осуществлять плавный переход от нечеткого множества к четкому.

Описание функции:

y = gbellmf(x, [a b c] )

Функция “обобщенный колокол” зависит от трех параметров и имеет следующую аналитическую запись:

,

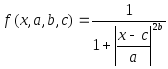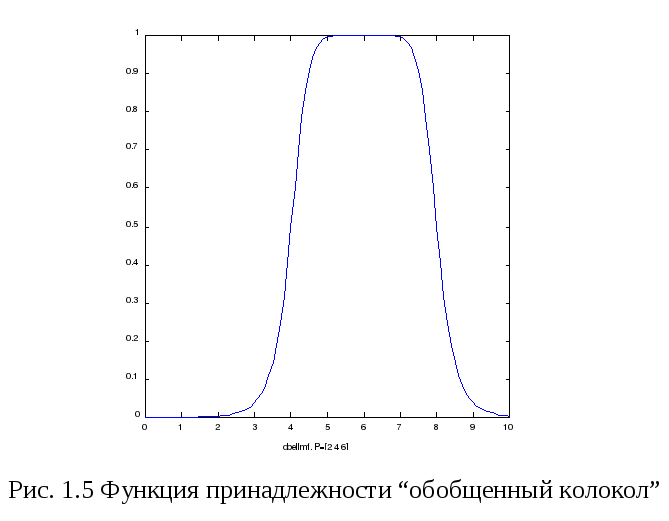
где параметр - определяет расположение центра ФП, а параметры и оказывают влияние на форму кривой (рис.1.5).

Пример 1.4

x=0:0.1:10;

y=gbellmf(x,[2 4 6]);

plot(x,y)

xlabel('gbellmf, P=[2 4 6]')

Благодаря их гладкости и простоты записи, ФП на основе функции распределения Гаусса и ФП “обобщенный колокол” являются наиболее часто используемыми при описании нечетких множеств. Дополнительным достоинством указанных функций является неравенство их значений нулю на всем базовом множестве.

Несмотря на то, что Гауссовские и колоколообразные ФП обладают свойством гладкости, они не позволяют формировать ассимметричные ФП. Для этих целей в MATLAB был предусмотрен набор функций сигмоидных функций. Соответствующие ФП могут быть открыты либо слева, либо справа в зависимости от типа функции. Симметричные и закрытые функции могут быть синтезированы с использованием двух дополнительных сигмоидных функций. Основная сигмоидная ФП обозначается sigmf, а дополнительные - dsigmf и psigmf.

Описание функции:

y = sigmf(x,[a c])

В аналитической форме сигмоидная функция sigmf записывается следующим образом:

. (*)

В зависимости от знака параметра данная ФП будет открыта или справа или слева (рис. 1.6, а), что позволяет применять ее при описании таких нечетких понятий, как “очень большой”, “крайне отрицательно” и других.

Описание функции:

y = dsigmf(x,[ ])

ФП dsigmf зависит от четырех параметров , , и и определяется как разность двух сигмоидных функций (*): (рис. 1.6, б)

Описание функции:

y = psigmf(x,[ ])

ФП psigmf также как и предыдущая функция зависит от четырех параметров , , и и определяется как произведение двух сигмоидных функций (*): (рис. 1.6, в)

Пример 1.5

x=0:0.1:10; Определяется базовое множество

subplot(1,3,1); Формируется матрица графиков (31) (1-й элемент - текущий

y=sigmf(x,[2 4]);

plot(x,y) Вывод графика в первый элемент матрицы

xlabel('sigmf, P=[2 4]')

subplot(1,3,2); Выбор второго текущего элемента

y=dsigmf(x,[5 2 5 7]);

plot(x,y) Вывод графика во второй элемент матрицы

xlabel('dsigmf, P=[5 2 5 7]')

subplot(1,3,3); Выбор третьего текущего элемента

y=psigmf(x,[2 3 -5 8]);

plot(x,y) Вывод графика в третий элемент матрицы

xlabel('psigmf, P=[2 3 -5 8]')

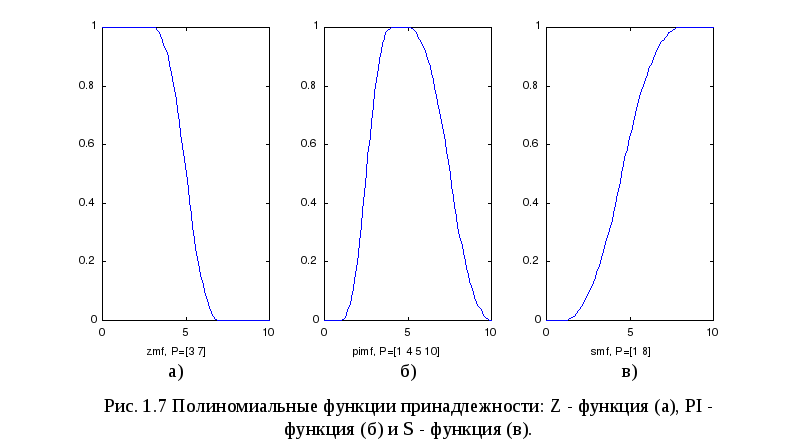
ИНЛ в составе MATLAB предоставляет возможность формирования ФП на основе полиномиальных кривых. Соответствующие функции называются Z - функции (zmf), PI - функции (pimf) и S - функции (smf). Функция zmf представляет собой ассимметричную полиномиальную кривую, открытую слева (рис.1.7, а), функция smf - есть зеркальное отображение функции zmf (рис. 1.7, б). Соответственно функция pimf равна нулю на правом и левом пределах и принимает значение, равное единице, на некотором отрезке в середине (рис. 1.7, в).

Описание функции:

y = zmf(x,[a b])

Параметры и определяют экстремальные значения кривой (рис. 1.7, а).

Описание функции:

y = pimf(x,[a b c d])

Параметры и определяют переход функции в нулевое значение, а параметры и - в единичное (рис. 1.7, б).

Описание функции:

y = smf(x,[a b])

Параметры и определяют экстремальные значения кривой (рис. 1.7, в).

Пример 1.6

x=0:0.1:10;

subplot(1,3,1);

y=zmf(x,[3 7]);

plot(x,y)

xlabel('zmf, P=[3 7]')

subplot(1,3,2);

y=pimf(x,[1 4 5 10]);

plot(x,y)

xlabel('pimf, P=[1 4 5 10]')

subplot(1,3,3);

y=smf(x,[1 8]);

plot(x,y)

xlabel('smf, P=[1 8]')

Помимо рассмотренных выше функций, позволяющих представлять нечеткие множества, в ИНЛ имеется возможность формировать собственные ФП или модифицировать встроенные.