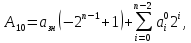37. Определение понятия – «машинное слово».

Машинное слово - упорядоченный набор цифр, букв и т. д., хранящихся в памяти ЭВМ и воспринимаемых при обработке устройствами машины как единое слово, команда. Количество основных символов в машинном слове называется длиной слова. Обычно машинное слово содержит целое число байтов.

38. Представление двоичного сигнала в эвм.

В какой бы форме не представлялась подлежащая обработке информация, она должна быть переведена компьютером на язык, доступный для автоматической обработки. Язык компьютера – это язык чисел, причем не обычных (десятичных), а двоичных, алфавит которых состоит всего лишь из двух цифр – 0 и 1.

Двоичная система наиболее проста и удобна для обработки на ЭВМ, т. к. компьютер – электрическая машина и работает с электрическими сигналами: есть сигнал – включено, нет сигнала – выключено.

В современной вычислительной технике информация как раз и кодируется с помощью сигналов двух видов: включено или выключено. Все входные сигналы, поступающие в компьютер, преобразуются в нули и единицы, при этом 0 означает отсутствие тока (нет сигнала, т. е. выключено), а 1 – присутствие тока в цепи (есть сигнал, т. е. включено). Принято обозначать одно состояние цифрой 0, а другое – цифрой 1. Такое кодирование называется двоичным, а цифры 0 и 1 называются битами

На этом простом принципе и основана работа ЭВМ. Любая информация в компьютере может быть представлена в виде последовательности двоичных символов – бит.

39. Формы представления двоичных чисел в эвм. Прямой,

обратный и дополнительный коды.

В вычислительных машинах применяются две формы представления двоичных чисел:

• Естественная форма, или форма с фиксированной запятой (точкой);

• Нормальная форма, или форма с плавающей запятой (точкой);

С фиксированной запятой все числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой (точкой), отделяющей целую часть от дробной. В общем случае разрядная сетка ЭВМ с фиксированной запятой имеет вид, показанный на рисунке:

знак	2n-1	…	21	20
n+1

2-1	2-2	…	2-r
r

Диапазон представления чисел по модулю для такой формы:

2^-r ≤ |N| ≤ 2ⁿ - 2^-r

С плавающей запятой каждое число изображается в виде двух групп цифр. Первая группа цифр называется мантиссой, вторая – порядком, причем абсолютная величина мантиссы должна быть меньше 1, а порядок – целым числом. В общем случае число в форме с плавающей запятой может быть представлено в виде:

N = ± Mp^±S

Прямой код. Прямой n-разрядный двоичный код отличается от двоичного тем, что в нем отводится один, как правило, самый старший разряд для знака, а оставшиеся n – 1 разрядов – для значащих цифр. Значение знакового разряда равно 0 для чисел А₂>0, и 1 – для чисел А₂<0.

Дополнительный код. Использование чисел со знаком (прямого кода представления чисел) усложняет структуру ЭВМ. В этом случае операция сложения двух чисел, имеющие разные знаки, должна быть заменена на операцию вычитания меньшей величины из большей и присвоения результату знака большей величины. Поэтому в современных ЭВМ, как правило, отрицательные числа представляют в виде дополнительного или обратного кода, что при суммировании двух чисел с разными знаками позволяет заменить вычитание на обычное сложение и упростить тем самым конструкцию арифметико-логического устройства компьютера.

Смысл перевода отрицательных чисел из прямого в дополнительный и обратный коды поясним на примере с десятичными числами. Допустим, вычислительная машина, которая оперирует с 2-разрядными десятичными числами, должна сложить два числа: X₁ = 84 и X₂ = -32. Заменим код отрицательного слагаемого X₂ его дополнением до 100, так что [X₂]_доп = 100 + X₂ = 68. Сложив числа X₁ + [X₂]_доп, получим:

Y = X₁ + [X₂]_доп = 84 + 68 = 1 52.

Обратный код. Для представления отрицательных чисел используется также обратный код, который получается инвертированием всех цифр двоичного кода абсолютной величина числа: ноли заменяются единицами, а единицы – нолями. При этом необходимо помнить, что все операции с отрицательными числами выполняются в формате машинного слова. Это значит, что к двоичному числу слева дописываются ноли до нужного количества разрядов. Например, для 8-разрядного машинного слова:

Число: -1 Код модуля числа: 00000001 Обратный код числа: 11111110

Число: -127 Код модуля числа: 01111111 Обратный код числа: 10000000

1

0

0

0

0

0

0

0

1

1

1

1

1

1

1

0

Для обратного кода справедливо следующее соотношение: