
- •Основные понятия
- •Скалярное поле
- •Предел функции нескольких переменных
- •Дифференцирование функций нескольких переменных Частные производные
- •Условия дифференцируемости
- •Производная по направлению
- •Дифференцирование сложной функции
- •Инвариантность формы полного дифференциала
- •Нормаль и касательная плоскость к поверхности
- •Геометрический смысл полного дифференциала функции двух переменных
- •Производная функции, заданной неявно
- •Производные и дифференциалы высших порядков
- •Частные производные высших порядков
- •Дифференциалы высших порядков
- •Операторная форма дифференциалов высших порядков
- •Формула Тейлора
- •Экстремумы функций нескольких переменных Точки максимума и минимума
- •Необходимое условие экстремума
- •Достаточные условия экстремума
- •Условный экстремум
- •Методы нахождения условного экстремума Метод исключения переменных
- •Метод неопределенных множителей Лагранжа
- •Геометрический смысл условного экстремума функции:
- •Наибольшие и наименьшие значения
- •Составители
- •Функции нескольких переменных Методические указания к самостоятельному изучению соответствующего раздела курса математики для студентов всех специальностей
Производная по направлению
Пусть
заданы функция
 ,
определенная в некоторой окрестности
точки
,
определенная в некоторой окрестности
точки
 , и
, и — единичный вектор
— единичный вектор
 .
.
Через
точку
 проведем прямую в направлении вектора
проведем прямую в направлении вектора
 и обозначим
и обозначим
 приращение функции, которое она получает
при смещении из точки
приращение функции, которое она получает
при смещении из точки
 в некоторую точку
в некоторую точку
 на этой прямой. Обозначим
на этой прямой. Обозначим
 – приращение функции в направлении
– приращение функции в направлении
 (рис.9).
(рис.9).




x

a

Рис.9
Производной
функции
 в точке
в точке
 по направлению
по направлению
 называется предел отношения
называется предел отношения
 к
к
 при
при

Обозначение

Производная по направлению характеризует скорость изменения функции в данной точке в данном направлении.
Составим формулу для производной по направлению. Для этого используем параметрические уравнения прямой:

где
 ,
,
 и
и
 — единичный направляющий вектор прямой.
Переменная
— единичный направляющий вектор прямой.
Переменная
 .
.
Проекция
функции
 на данную прямую есть функция
на данную прямую есть функция
 одной переменной
одной переменной
 :
:

причем
 ).
Тогда из определения (3) следует, что
).
Тогда из определения (3) следует, что

Для
трехмерного пространства когда
 получим,
получим,

где
 — углы, образованные вектором
— углы, образованные вектором

с осями координат. Тогда параметрические уравнения прямой имеют вид

Находим
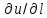 в точке a
по формуле (4). Для этого дифференцируем
функцию вида
в точке a
по формуле (4). Для этого дифференцируем
функцию вида

как
сложную функцию от
 при
при
 .
Получим
.
Получим

Производная
n-мерной
функции
 в точке
в точке
 в направлении единичного вектора
в направлении единичного вектора
 вычисляется аналогично. Получим
вычисляется аналогично. Получим

Таким образом геометрический смысл производной по направлению функции двух переменных следующий :

В
Z=U(x,y)



N

A
M
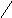
Рис.10
На
рис. 10 изображена поверхность
 ,
точка
,
точка
 и вектор
и вектор

Проведем
числовую ось
 через точку
через точку
 параллельно вектору
параллельно вектору
 .
Начало отсчета на этой оси выберем в
точке
.
Начало отсчета на этой оси выберем в
точке
 .
Положение любой точки на оси определяется
числом
.
Положение любой точки на оси определяется
числом
 .
Проведем плоскость
.
Проведем плоскость
 через ось
через ось
 параллельно оси
параллельно оси
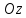 .
Плоскость
.
Плоскость
 пересекает график функции
пересекает график функции
 по кривой (АВ), изображенной на рис. 10.
Эта кривая является графиком функции
по кривой (АВ), изображенной на рис. 10.
Эта кривая является графиком функции

Касательная
(MN) к графику функции
 в точке
в точке
 образует с положительным направлением
оси
образует с положительным направлением
оси
 некоторый угол
некоторый угол
 .
Получим
.
Получим

Градиент
Пусть
функция
 в точке
в точке
 частные производные по всем переменным.
частные производные по всем переменным.
Тогда вектор
 ,
,
или
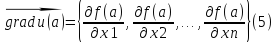
называется
градиентом
(вектором–градиентом) функции
 в точке
в точке
 .
.
Вектор–градиент
(5) обозначается символом
 или
или
 .
Символ
.
Символ
 читается как «намбл». Называется оператор
намбла
читается как «намбл». Называется оператор
намбла
Для случая трех переменных получим соответственно:

Свойства градиента:
Пусть
 и
и
 функции дифференцируемы в некоторой
точке
функции дифференцируемы в некоторой
точке
 .
Тогда в этой точке градиент имеет
свойства:
.
Тогда в этой точке градиент имеет
свойства:




где
 ,
- постоянная величина,
,
- постоянная величина,
 и
и
 – функции n
переменных.
– функции n
переменных.
Связь градиента с производной по направлению
Производная
функции
 в направлении единичного вектора
в направлении единичного вектора
 вычисляется по формуле
вычисляется по формуле

Используя определение градиента и формулу для скалярного произведения (в ортонормированном базисе), получим:

Свойство инвариантности градиента
Так
как
 , из формулы (6) следует, что
, из формулы (6) следует, что

где
 — угол между векторами
— угол между векторами
 и
и
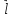 в данной точке.
в данной точке.
Из
формулы (7) следует, что наибольшая
скорость изменения функции
 достигается в направлении ее градиента
достигается в направлении ее градиента
 и равна норме (модулю) градиента -
и равна норме (модулю) градиента -
 .
Это доказывает, что вектор
.
Это доказывает, что вектор
 не зависит от выбора системы координат
(инвариантность).
не зависит от выбора системы координат
(инвариантность).
Сложные функции нескольких переменных
Понятие сложной функции
Пусть
функция
 определена в некоторой окрестности
точки
определена в некоторой окрестности
точки
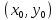 . Пусть ее аргументы
. Пусть ее аргументы
 и
и
 в свою очередь являются функциями
в свою очередь являются функциями
 ,
,
 и определены в некоторой окрестности
точки
и определены в некоторой окрестности
точки
 ,
причем
,
причем
 .
.
Тогда
в окрестности точки
 определена сложная
функция
аргумента
определена сложная
функция
аргумента
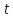

Подобным образом определяются сложные функции любого числа переменных.
Например,
если
 и
и
 — функции 2–х переменных:
— функции 2–х переменных:
 и
и
 , то функция
, то функция
 является сложной функцией двух переменных
является сложной функцией двух переменных
 и
и
 :
:

