2.Метод анализа иерархии т. Саати

Иерархический анализ систем проводится в последовательности, показанной на схеме рис.8.1.

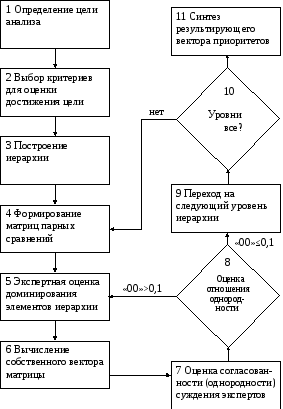
Рис.8.1. Схема анализа иерархии систем по методу Т. Саати

3.Построение иерархии

Формируется решаемая проблема (задача). Для решения этой проблемы строится иерархия, включающая цель, расположенную в вершине (фокус), промежуточные уровни (критерии, процессы) и альтернативы (искомые решения), формирующие самый низкий иерархический уровень. На рис.8.2 в качестве примера приведена иерархия, построенная с целью определения значимости основных процессов организации с точки зрения удовлетворения нужд и ожидания всех заинтересованных сторон.

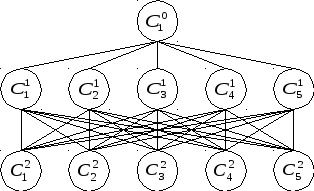
Рис.8.2. Иерархия для оценки значимости процессов организации

По международному стандарту ИСО 9004:2000 степень удовлетворенности всех заинтересованных сторон является глобальным критерием эффективности системы качества любой организации. Поэтому на рис.8.2 первый уровень иерархии (фокус) имеет одну цель: – эффективность и конкурентоспособность организации располагается на вершине иерархии (в фокусе), на втором (промежуточном) уровне располагаются заинтересованные стороны организации: – потребители; – работники; – поставщики; – владельцы; – общество. На последнем (третьем) уровне иерархии располагаются альтернативы – основные группы (классы) существующих в организации процессов: – подразделения; – менеджмента качества; – бизнес-процессов; – безопасности труда; – охраны окружающей среды. Целями третьего уровня являются удовлетворение нужд и ожиданий заинтересованных сторон, помещенных на втором уровне иерархии.

На рис.8.3 в качестве примера приведена иерархия задачи выбора оптимальной стратегии предприятия в области качества (содержание этой схемы см. на рис.11 в книге Горленко О.А., Мирошников В.В. «Создание систем менеджмента качества в организации»).

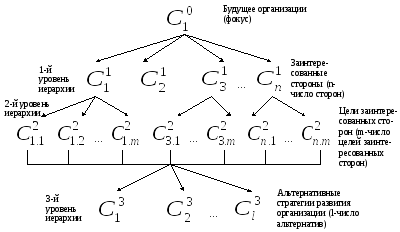
Рис.8.3. Иерархия задачи выбора оптимальной стратегии предприятия в области качества

Лекция 9

Матрицы парных сравнений

1.Понятие о матрицах парных сравнений

После построения иерархии производится сравнение значимости ее элементов. Сравнение этих элементов производится с помощью матриц парных сравнений, которые имеют следующий вид (рис.9.1).

Сj Ci	C1	C2	C3	C4	C5	C6	C7	…	CN
C1	а11	а12	а13	а14	а15	а16	а17	…	а1N
C2	а21	а22	а23	а24	а25			…
C3	а31	а32	а33					…
C4				а44
C5					а55
C6						а66
C7							а77
…								…	…
CN	aN1	aN2	aN3	aN4					аNN

Рис.9.1. Матрица парных сравнений

Матрицы парных сравнений строятся следующим образом. Обозначим через , сравниваемую пару элементов, (k =0, 1, 2, …, q), q – общее число уровней иерархии; i – номер элемента, который сравнивается с элементом, имеющим номер j на том же (k+1) уровне иерархии (i,j = 1, 2 … N), N – число элементов на (k+1) уровне иерархии.

Обозначим через а_ij число, соответствующее значимости элемента по сравнению с относительно элемента , расположенного на вышестоящем k-том уровне иерархии. Элемент является в данном случае критерием доминирования элемента над , т.е. какой из двух сравниваемых элементов важнее, предпочтительнее, более вероятен, имеет большее воздействие. Тогда матрицу парных сравнений можно представить так:

, где

(9.1)

k – номер вышестоящего уровня иерархии;

n – номер элемента на k-том уровне, относительно которого определены оценки а_ij элементов и нижестоящего (k+1)-го уровня иерархии;

i и j – порядковые номера соответственно в строке и столбце матрицы .

Матрица (9.1) обладает свойством обратной симметрии, т.е. (9.2).