Векторная диаграмма:

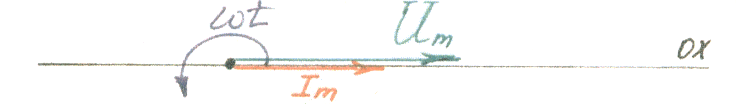
Закон Ома для данной цепи будет иметь вид:

Мощность в этой цепи:

т.к. тогда:

Среднее значение мошности за период:

т.к. (Вт)

т.к.

Среднее значение мощности Р в цепи переменного тока с сопротивлением R принято называть активной мощностью, а сопротивление R- активным сопротивлением.

Цепь переменного тока с индуктивностью L.

Такая цепь получится, если к зажимам генератора переменного тока подключить идеальную катушку индуктивности, т.е. катушку, обладающую только индуктивностью L.

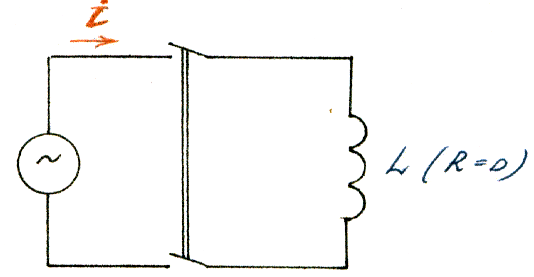
При замыканий рубильника по катушке будет проходить синусоидальный ток:

_m sin (А).

Этот ток создаст переменное магнитное поле, которое будет пронизывать витки этой катушки и индуктировать в ней эдс самоиндукции:

e_L =

Применяя второе правило Кирхгофа для рассматриваемой цепи можно записать:

Тогда: U_L + e_L = 0

т.к. то:

Таким образом, в цепи переменного тока с индуктивностью Ь при синусоидальном токе напря­жение будет тоже синусоидальным, но опережающим ток по фазе на угол 90° или %Т.

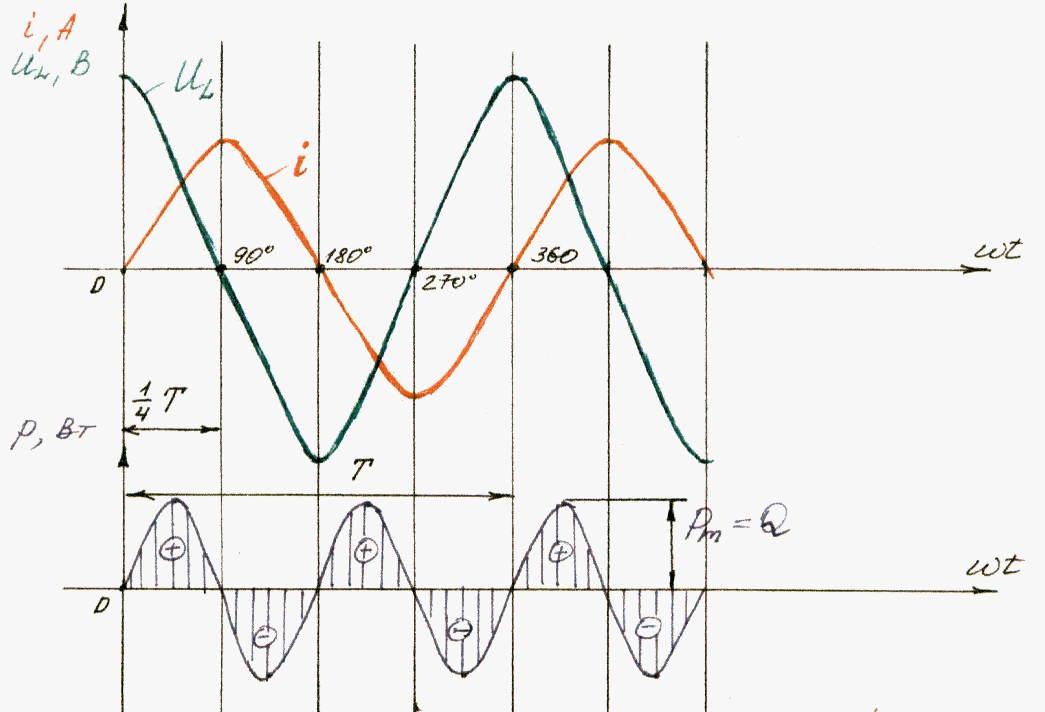
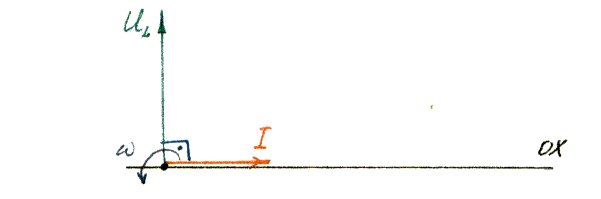
Векторная диаграмма будет иметь вид:

Масштаб: для токов

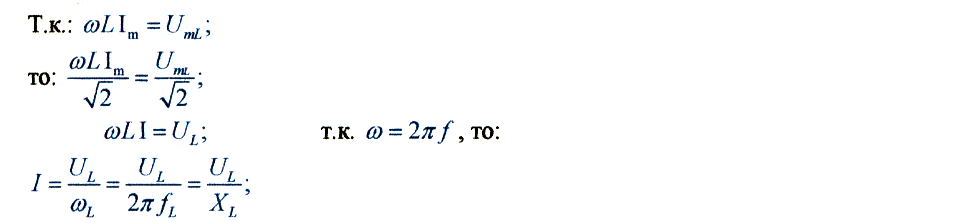
(А) – закон Ома для цепи с емкостью,

Пример:

Катушка, обладающая индуктивностью L = 0,0127Гн, включена в сеть переменного тока с час­тотой 50 Гц и напряжением 40 В. Определить ток, проходящий по катушке и ее реактивную мощ­ность.

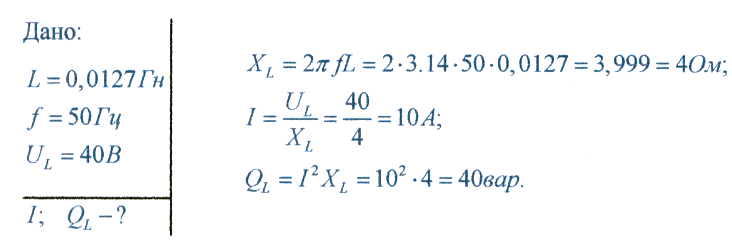
Цепь переменного тока с емкостью С.

Такая цепь получится, если к зажимам генератора переменного тока подключить обыкновенный конденсатор, обладающий какой-то емкостью С.

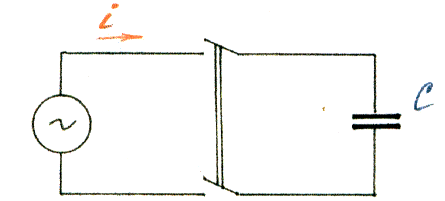
При замыкании рубильника к обкладкам конденсатора будет приложено синусоидальное на­пряжение:

(В)

На обкладках конденсатора будут накапливаться электрические заряды:

.

Ток в этой цепи:

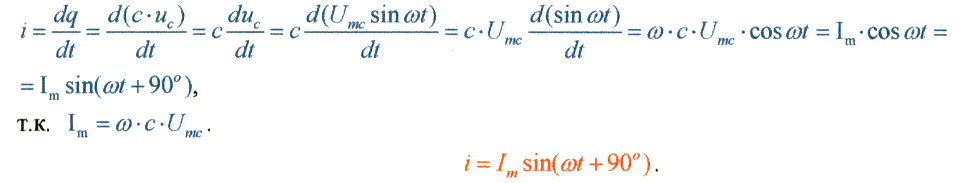
Таким образом, в цепи переменного тока с емкостью С при синусоидальном напряжении ток будет тоже синусоидальным, но опережающим напряжение по фазе на угол 90º или Т.

Векторная диаграмма для данной цепи:

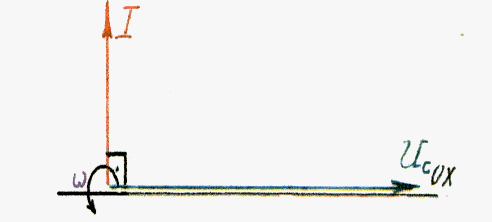
Т.к. , то:

;

— (А) - закон Ома для цепи с емкостью С,

где (Ом) - реактивное сопротивление емкости или емкостное сопротивление.

Мощность в этой цепи:

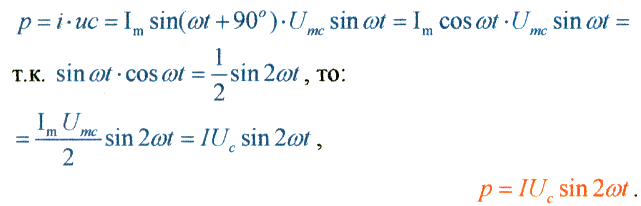
Максимальное значение мощности за период в цепи с емкостью принято называть реактивной мощностью .

(вар;квар)

Пример:

Конденсатор емкостью 80 мкФ подключен в сеть переменного тока с частотой 50 Гц и напря­жением 400 В. Определить ток и реактивную мощность в цепи.

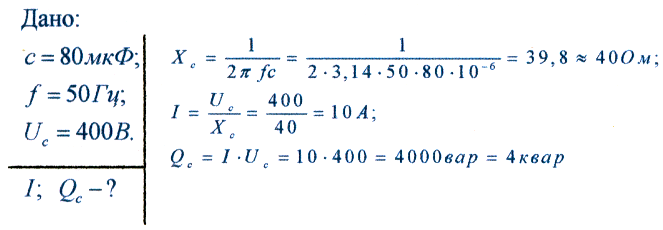
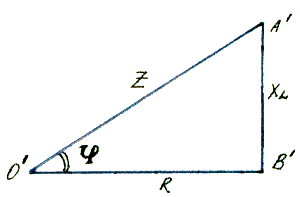
Треугольник О'А'В' - это треугольник сопротивлений, который подобен треугольнику напря­жений (∆ОАВ). Поэтому угол φ, заключенный между катетом R и гипотенузой Z. будет тот же угол сдвига по фазе между током I и напряжением, приложенным ко всей цепи, U, который для этого тре­угольника можно определить через:

и

В рассматриваемой цепи следует различать три мощности:

1. активную мощность:

(Вт)

2. реактивную мощность:

(вар)

3. полную мощность:

(ВА)

где ВА - вольтампер.

Эти три мощности также связаны между собой, как стороны прямоугольного треугольника, ка­тетами у которого являются Р и Q_L, а гипотенузой - S.

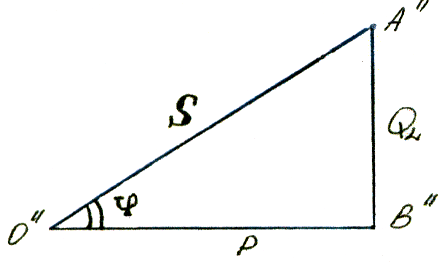
По теореме Пифагора для треугольника О" А"В":

(ВА)

∆О"А"В" - треугольник мощностей, который подобен треугольнику напряжений и треуголь­нику сопротивлений. Поэтому угол φ, заключенный между катетом Р и гипотенузой S - это тот же угол сдвига по фазе между током и напряжением, приложенным ко всей цепи, который определяется через:

где соsφ - коэффициент мощности, показывающий, какая часть из полной мощности будет активной (полезной) мощностью.

Цепь переменного тока с активным сопротивлением R и индуктивностью L.

Такая цепь получится, если к зажимам генератора переменного тока подключить реальную ка­тушку индуктивности, обладающую активным сопротивлением R(электрическим сопротивлением провода) и индуктивностью L.

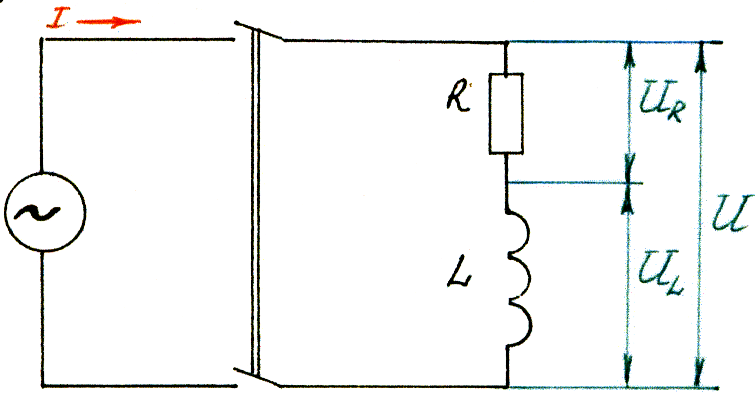
При замыкании рубильника в цепи возникает ток, который, проходя через каждый элемент этой цепи, будет создавать на них падения напряжений:

1) на активном сопротивлении: - активное напряжение, совпадающее по

фазе с током;

2. на индуктивности: 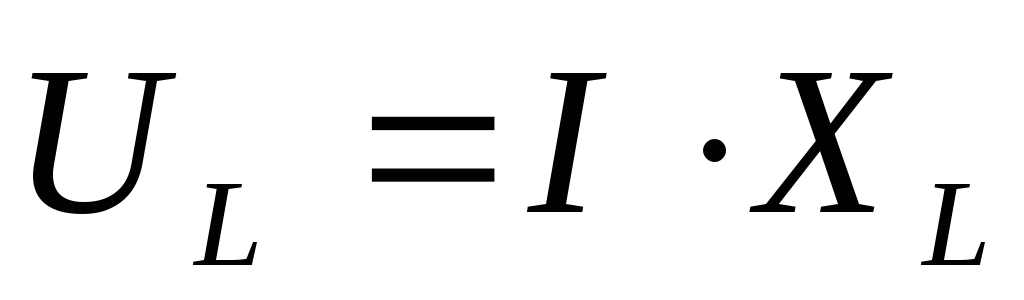- индуктивное напряжение, опережающее ток по

фазе на угол 90°

Для определения напряжения U, приложенного ко всей цепи, строим векторную диаграмму:

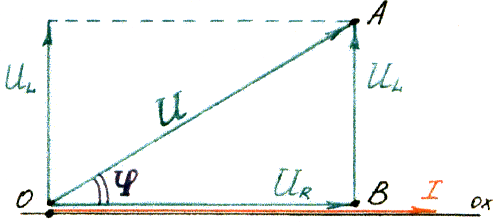
По теории Пифагора: ;

.

В векторной диаграмме ∆ОАВ — треугольник напряжений, в котором угол φ — это угол сдвига по фазе между током I и напряжением U, приложенным ко всей цепи, можно определить через:

а также tg φ =; φ = ψ_i – ψ_u, где ψ_i – ψ_u - начальные фазные углы тока и напряжения.

Из последнего выражения следует, что полное сопротивление цепи Z и его составляющие R и Х_L, связаны между собой, как стороны прямоугольного треугольника, катетами у которого являются R и Х_L, а гипотенузой - Z.

Пример:

Катушка, обладающая активным сопротивлением R=8OM и индуктивностью L=0,0191Гн, включена в сеть переменного тока с частотой 50 Гц под напряжение 200 В. Определить: I; U_r; U_l; Р; Q; S; соsφ.

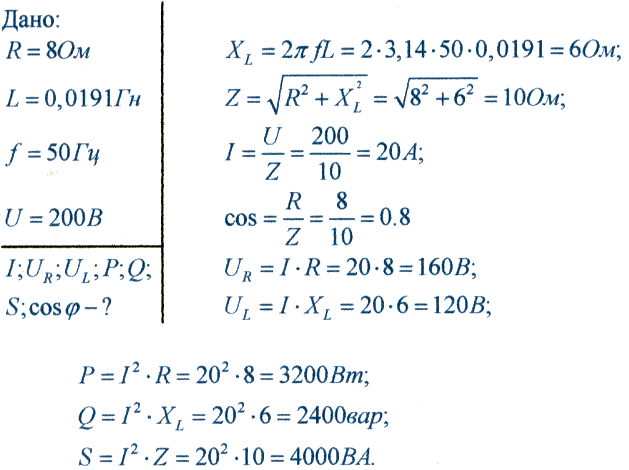
Неразветвленная цепь переменного тока с активным сопротивлением, индуктивностью и емкостью.

Такая цепь получится, если в сеть переменного тока подключить последовательно соединенные между собой катушку и конденсатор.

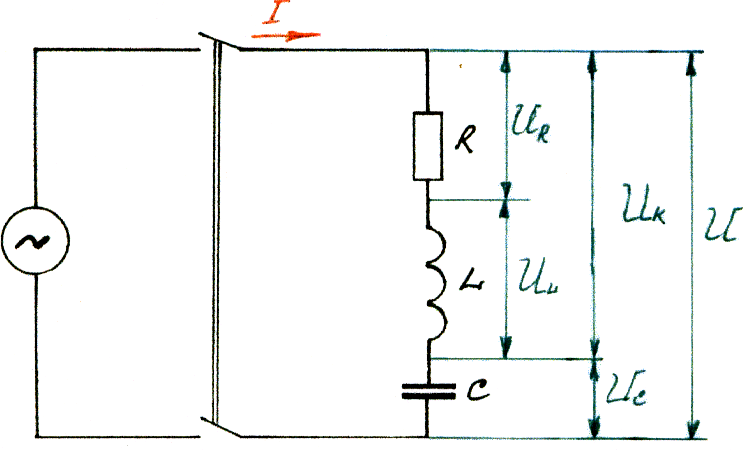
При замыкании рубильника в цепи возникнет ток, который на каждом из элементов цепи будет создавать падение напряжений:

1) на активном сопротивлении:, совпадающие по фазе с током, т.е. φ = 90°;

2) на индуктивности:, опережающее ток по фазе на угол φ = 90° (Т);

3) на емкости:, отстающее по фазе от тока на угол φ = 90°.

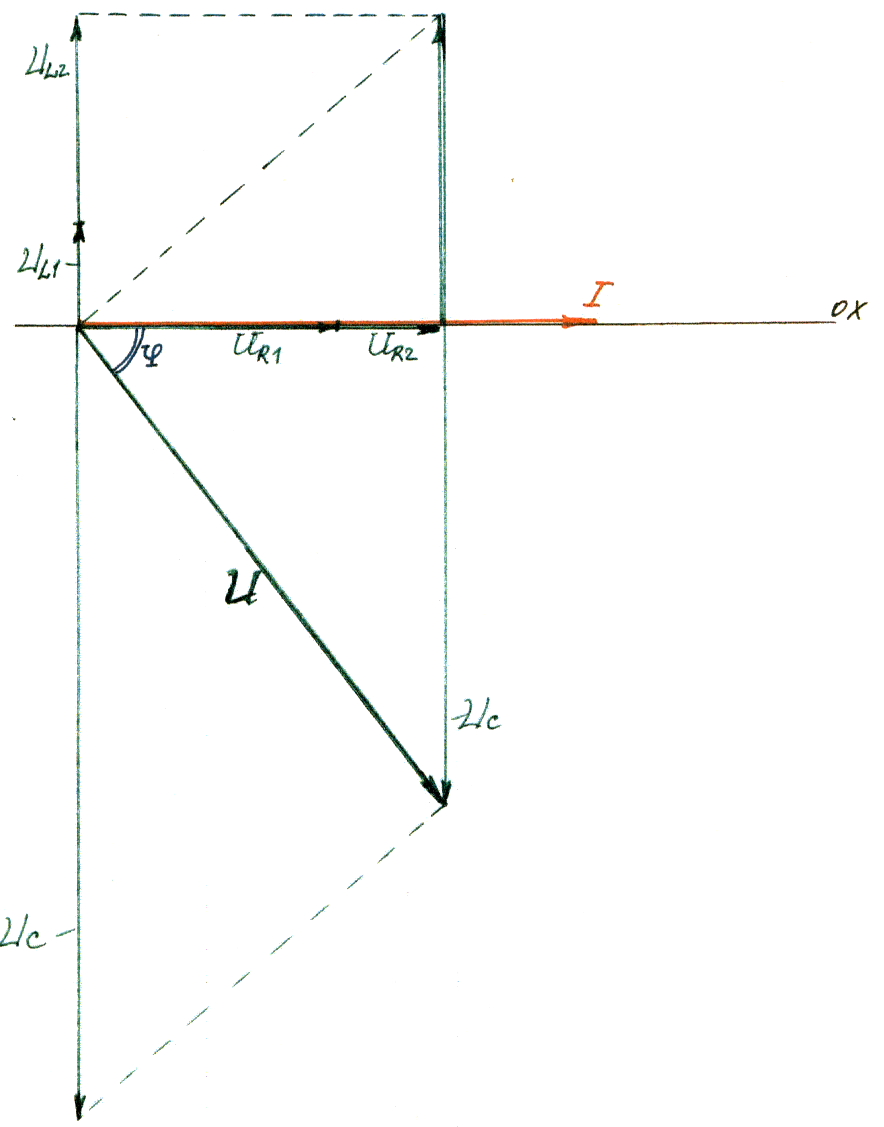
Для определения общего напряжения строим векторную диаграмму:

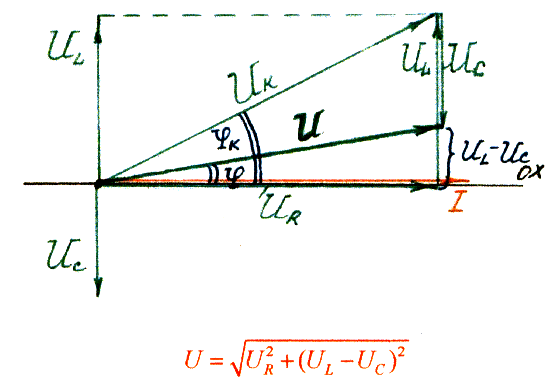
Учитывая, что: ; ,

тогда:

отсюда закон Ома для данной цепи будет иметь вид: (А),

где (Ом) - полное сопротивление для рассматриваемой цепи.

В этом случае:

Если же неразветвленная цепь переменного тока будет содержать в себе несколько активных и несколько реактивных элементов, тогда:

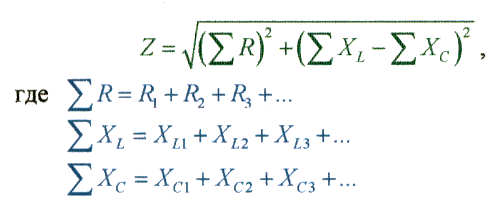
Мощности в неразветвленной цепи:

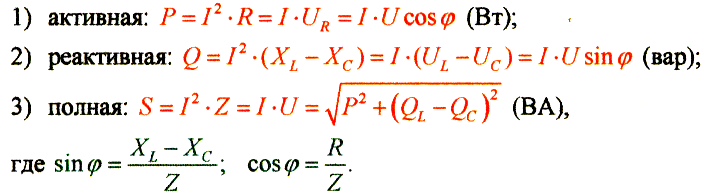
Если реактивная мощность Q имеет положительное значение «+», то это значит, что цепь по­требляет электроэнергию.

Если реактивная мощность Q имеет отрицательное значение «-», то цепь отдает энергию гене­ратору. Если же Q = 0, тогда цепь не потребляет и не отдает энергию.

Пример:

Катушка с активным сопротивлением 8 Ом и индуктивностью 0,274 Гн соединена последова­тельно с конденсатором емкостью 40 мкФ и включена в сеть переменного тока с частотой у=50 Гц под напряжение 200 В. Определить: I;U_a;U_L;U_c;P;Q;S;cosφ.

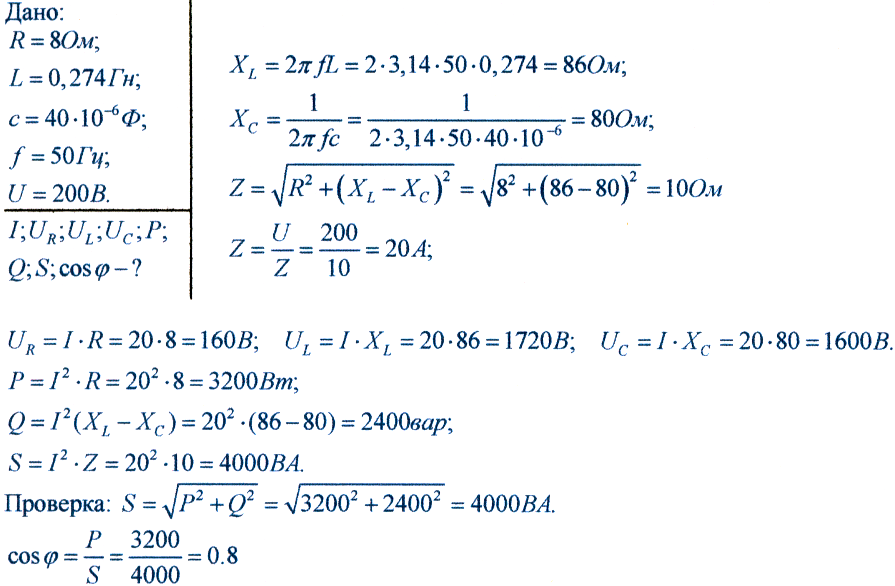
Резонанс напряжений.

В цепи с последовательным соединением активного сопротивления R, индуктивности L и ем кости С напряжение приложенное ко всей цепи может:

1) опережать ток по фазе на какой-то угол φ, если u_l>u_c или x_l>x_c:

2) отставать от тока по фазе на какой-то угол φ, если u_l>u_c или x_l>x_c:

3) совпадать по фазе с током (φ = 0), если u_l>u_c или x_l>x_c:

В этом случае в цепи наступает резонанс напряжений, условием которого является равенство реактивных сопротивлений:

Х_L=Х_С.

При резонансе напряжений:

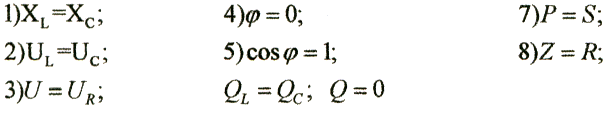
9) Ток в цепи достигает наибольшего своего значения для рассматриваемой

цепи.

Пример:

Для ниже приведенной схемы определить: I; UR; UL; UC; P; Q; S; соsφ, если известно, что:

\

Порядок построения векторной диаграммы:

а) откладываем вектор тока по оси ординат (ОХ);

б) т.к. вектор напряжения на активном сопротивлении и вектор тока совпадают, то векторы на­пряжения на активных сопротивлениях откладываем параллельно вектору тока;

в) т.к. вектор напряжения на индуктивности опережает вектор тока на угол φ = 90°, то векторы напряжений на индуктивностях строим перпендикулярно вверх к вектору тока;

г) т.к. вектор напряжения на индуктивности отстает от вектора тока на угол φ = 90°, то вектор напряжения на емкости откладываем перпендикулярно вниз вектору тока;

д) проводим геометрическое суммирование векторов напряжений по правилу параллелограмма, результирующим будет вектор напряжения, приложенного ко всей цепи, начало которого будет совпадать с началом первого вектора активного напряжения, а конец - с концом вектор; напряжения на емкости.

Разветвленная цепь переменного тока с активным сопротивлением R, ин­дуктивностью L и емкостью С.

Такая цепь получится, если к зажимам генератора переменного тока подключить параллельно соединенные между собой реальную катушку индуктивности и конденсатор.

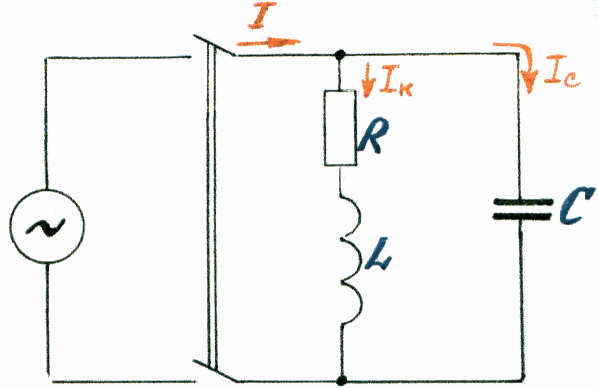
При замыкании рубильника в каждой из параллельных ветвей будут протекать токи:

1) ток в катушке: где — отстающий по фазе от напряжения на какой-то угол φ_к

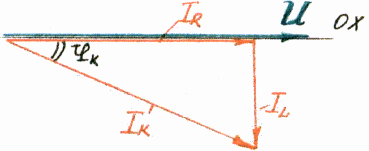
Этот угол можно определить через:

откуда токи:

и

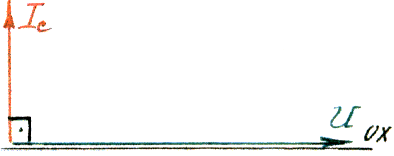
2) ток во второй ветви – это чисто емкостной ток:

, где опережающий по фазе напряжение на угол 90°.

Для определения тока, протекающего по всей цепи, строим общую векторную диаграмму:

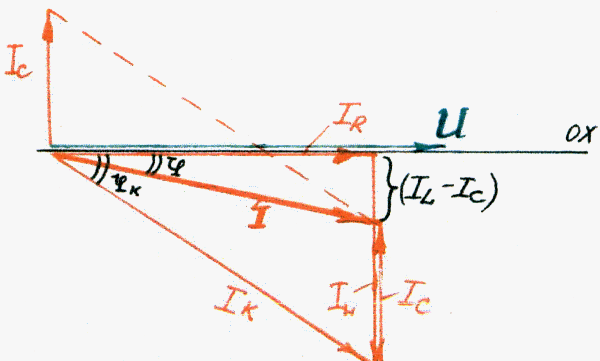
Общий ток в этой цепи будет определяться по формуле:

Угол сдвига по фазе tp можно определить через:

Мощность в такой цепи:

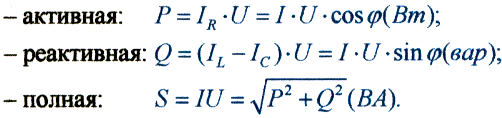
Пример:

Катушка, обладающая активным сопротивлением 8 Ом, индуктивным сопротивлением x_l= 6 Ом, соединена параллельно с конденсатором емкостью 80мкФ. Они включены в сеть переменно­го тока с частотой 50 Гц и напряжением 400 В.

Резонанс токов.

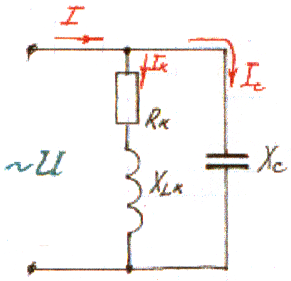
В рассматриваемой цепи общий ток может:

1) отставать по фазе от напряжения на какой-то угол φ, если I_L >I_C:

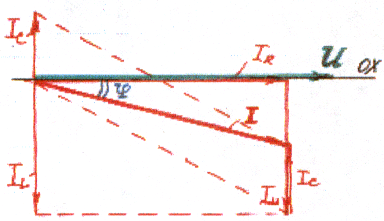
2) опережать напряжение по фазе на какой-то угол φ, если I_L <I_C:

3) совпадать по фазе с напряжением (φ=0), если I_L =I_C:

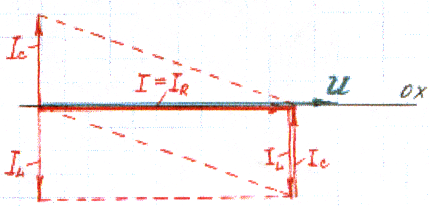
В этом случае в рассматриваемой цепи наступает резонанс токов, при котором:

1. φ = 0

2. cos φ = 0

3. Q = 0

4. P = S,

5. Ток, протекающий по всей цепи, I=I_R и достигает своего самого наименьшего возможного значения.

Расчет цепей переменного тока символическим методом.

Для расчета сложных цепей переменного тока со смешанным соединением активных и реактивных сопротивлений используется символический метод, основанный на применении комплексных чисел.

Сущность метода сводится к тому, что все параметры цепи (полные сопротивления; токи; напряжения; полные мощности) записываются в комплексной форме, что позволяет заменить все действия над векторами на алгебраические действия над комплексными числами и приводит расчет сложной цепи переменного тока к подобию расчета цепи постоянного тока любым из известных методов (упрощения; уравнений Кирхгофа; контурных токов и т.д.).

Поэтому в комплексной форме полное сопротивление ветви электрической цепи будет иметь вид:

Z = R ± jX (Ом),

причем действительной частью этого комплекса будет активное сопротивление R, а мнимой реактивное сопротивление или емкости, или индуктивности. Знак перед мнимой частью означает, что, если: «+», то это индуктивное сопротивление, если «-»., то емкостное сопротивление.

Полная мощность в комплексной форме будет иметь вид:

S = IU = P+jQ (BA),

где Р - активная мощность, представляет действительную часть комплекса мощности;

JQ ~ реактивная мощность - мнимая часть комплекса мощности;

I - сопряженный комплекс тока.

Расчет цепи символическим методом рассмотрим на примере.

Пример

Для ниже приведенной цепи переменного тока со смешанным соединением активных и реактивных сопротивлений определить: токи в ветвях I₁; I₂; I₃ и общий ток в цепи; мощности S₁; S₂; S₃; Sобщ и cos . Построить векторную диаграмму токов и напряжений для всей цепи, если известно:

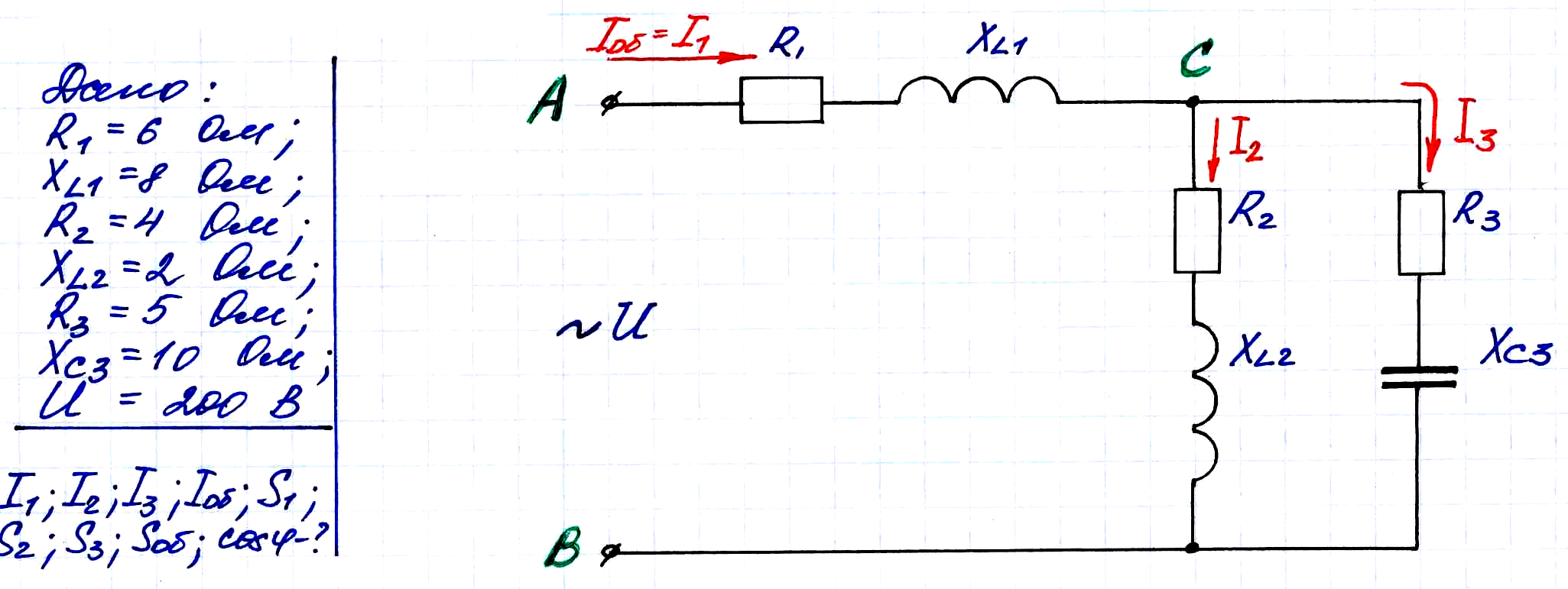
1) Запишем в комплексной форме полные сопротивления для отдельных участков данной цепи:

(Ом);

(Ом);

(Ом).

2) Применяя метод упрощения схемы, определим общее полное сопротивление для ветвей с Z₂

и Z₃ в комплексной форме:

т.к. Z₂ и Z₃ - соединены параллельно, то:

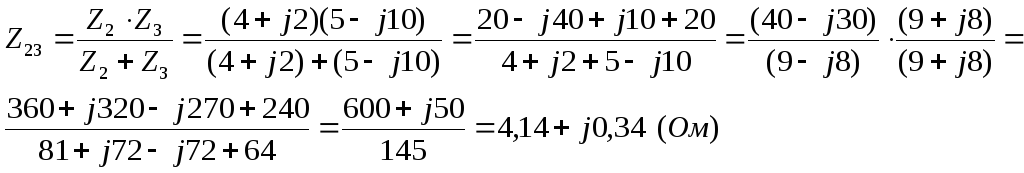
2. Определить комплекс общего сопротивления всей цепи:

т.к. Z₁ и Z₂₃ – соединены последовательно, то:

(Ом)

2. Определим общий ток цепи:

(Ом)

Так как Iобщ = I₁, то I₁ = 11,77 – j 9,68 (А)

5) Определим напряжение на отдельных участках цепи:

U₁ = I₁ ^. Z₁ = (11,77 – j 9,68) (6 + j8) = 70,62 + j94,16 – j58,08 + 77,44 = 148,06 + j36,08 (В);

так как ток I₁ протекает и через эквивалентное сопротивление Z₂₃, то:

U₂₃ = I₁ ^. Z₂₃ = (11,77 – j9,68) (4,14 + j0,34) = 48,7 + j4 – j40,08 + 3,29 = 52 – j36,08 (В).

6)Определим ток в ветвях с сопротивлениями Z₂ и Z₃:

(А)

(А)

7) Проверка:

для узла С по первому правилу Кирхгофа:

I₁=I₂+I₃;

11,77 – j 9,68 = 6,8 – j12,42 + 4,97 +j2,72

11,77 – j9,68 = 11,77 – j9,7 (А)

8)Определим мощности:

, Q₁ = 1857,88 вар.

(ВА),

где P₂ = 801,71 (Вт), Q₂ = 400,5 (Вар).

где P3 = 160,3 Вт, Q3 = - 320,76 вар

(BA),

где Pобщ = 2354 Вт, Qобщ = 1936 вар.

Определим модель комплекта общей мощности:

(BA)

9)Определим коэффициент мощности для всей цепи:

10)Для построения векторной диаграммы для данной цепи необходимо выбрать масштабы для токов и напряжений :

- для токов масштаб – m_i = 2 A/см;

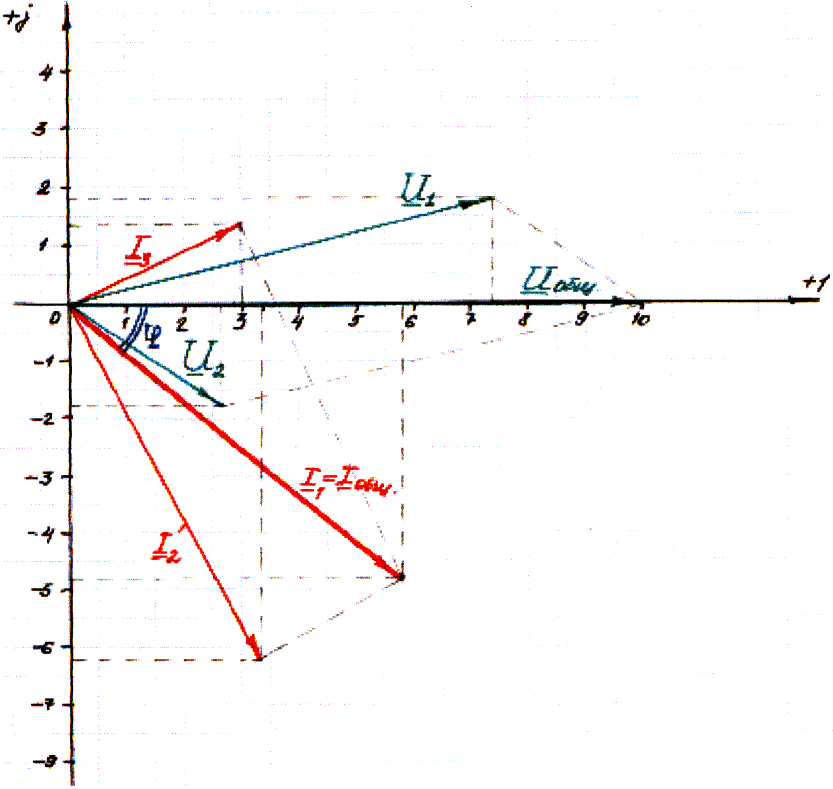
Угол сдвига по фазе между общим током и общим напряжением цепи определяем через: