Тема 5. Решение дифференциальных уравнений в системе Maple

Для нахождения решений дифференциальных уравнений используется команда dsolve. Рассмотрим характерные применения этой команды:

dsolve(eqns,vars) - решение уравнений eqns относительно переменных vars.

dsolve(eqns+inits,vars) - решение задачи Коши для eqns с начальными данными inits.

Можно также указывать дополнительные условия (option):

laplace - использовать трансформанту Лапласа;

series - применять разложение в ряды;

explicit - явно выражать решение через зависимую переменную;

numeric - численно решать дифференциальное уравнение.

При составлении уравнений для указания производной применяется команда diff, а команда D используется для обозначения производной при задании начальных или краевых условий.

Рассмотрим примеры задания системы дифференциальных уравнений и обращения к команде dsolve.

Рассмотрим примеры:

> deqn:=diff(y(x),x$2)+3*diff(y(x),x)+2*y(x);

> dsolve(deqn,y(x));

Здесь _C1 и _C2 - произвольные константы, через которые выражается решение и которые должны быть определены из дополнительных (начальных или краевых условий).

Зададим теперь краевые условия и решим то же уравнение еще раз.

> ini:=y(0)=0,y(1)=1;

> dsolve({deqn,ini},y(x));

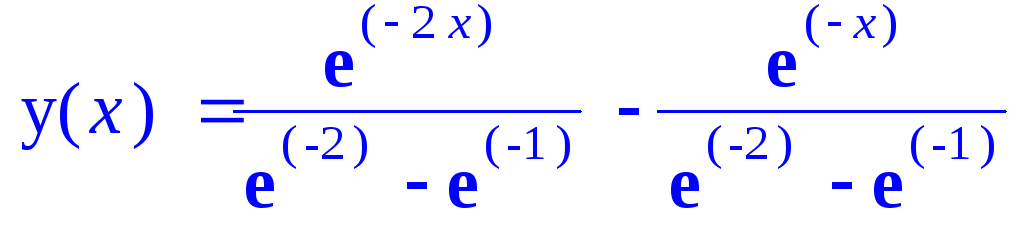
Все то же самое можно оформить несколько по-другому (численно, используя опцию numeric):

> deqn:=diff(y(x),x$2)+3*diff(y(x),x)+2*y(x);

> seqn:=dsolve({deqn, y(0)=0, y(1)=1},y(x),numeric);

Аргумент функции x_bvp указывает здесь на тот факт, что решается краевая задача (boundary value problem по независимой переменной x – x_bvp). Далее выведем полученное численное решение в нескольких характерных точках:

> seqn(0); seqn(0.25); seqn(0.5); seqn(0.75); seqn(1);

Зададим теперь не краевые условия для нашего уравнения, а начальные условия в точке x=0, причем второе условие будет соответствовать и решим повторно нашу задачу (в данной постановке речь идет о классической задаче Коши для обыкновенного дифференциального уравнения, а не о краевой задаче, для которой дополнительные (краевые) условия задаются на разных концах интервала, на котором ищется решение):

> deqn:=diff(y(x),x$2)+3*diff(y(x),x)+2*y(x);

> ini:=y(0)=0,D(y)(0)=1;

> dsolve({deqn,ini},y(x));

Если явное решение дифференциального урвнения не находится, то команда dsolve может быть запущена для поиска решения в виде разложения в ряд (опция series), методом преобразования Лапласа (опция laplace) или же численно (опция numeric).

Результатом работы команды dsolve с опцией numeric будет создание процедуры, к которой можно обращаться для вычисления отдельных значений или для построения графика решения на заданном промежутке решения:

> deqn:=diff(y(x),x$2)+3*diff(y(x),x)+2*y(x);

> ini:=y(0)=0,D(y)(0)=1;

> F:=dsolve({deqn,init},y(x),numeric);

Здесь указано, что численный метод method=rkf45, примененный здесь является разновидностью метода Рунге-Кутта 4-ого порядка точности (этот высокоточный метод применяется системой по умолчанию).

> F(.5);

> with(plots);

> plots[odeplot](F,[x,y(x)],0..10,labels=[x,y]);

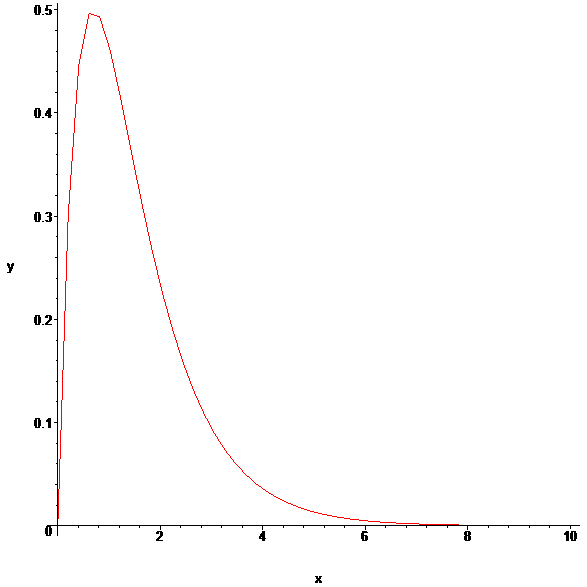
Отметим, что в приведенном примере для построения графика решения использована команда odeplot из пакета plots, который необходимо предварительно подключить (см. команду with(plots)).