-
Двойственные функции и принцип двойственности
Функция
называется двойственной к функции
f(x1,x2,…,xn).
Для обозначения двойственной функции
используется запись: [f(x1,x2,…,xn)]*
или f*(x1,x2,…,xn)
или f*.
Для получения столбца значений двойственной функции, как следует из определения, необходимо инвертировать значения функции f, т.е. заменить все единицы на нули, а нули – на единицы, а затем «перевернуть» полученный столбец, т.е. переписать его, начиная с конца, – что соответствует инвертированию значений переменных.
Пример: в таблице 13 процесс получения двойственной функции показан по шагам.
|
x |
y |
z |
f(x,y,z) |
|
|
|
|
0 |
0 |
0 |
1 |
0 |
0 |
|
|
0 |
0 |
1 |
1 |
0 |
1 |
|
|
0 |
1 |
0 |
0 |
1 |
1 |
|
|
0 |
1 |
1 |
1 |
0 |
1 |
|
|
1 |
0 |
0 |
0 |
1 |
0 |
|
|
1 |
0 |
1 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
0 |
1 |
0 |
|
|
1 |
1 |
1 |
1 |
0 |
0 |
Таблица 13 |
Легко
убедиться, что (0)*=1, (1)*=0,
(х)*=х, (
)*=
,
(x&y)*=
xy,
(xy)*=x&y,
(xy)*=
,
(
)*=yx,
(xy)*=xy,
(xy)*=xy,
(xy)*=xy,
(xy)*=xy.
Функция, совпадающая со своей двойственной, называется самодвойственной. Из перечисленных выше функций к самодвойственным относятся тождественная функция и отрицание.
Из определения двойственности следует, что f**=(f*)*=f, т.е. f двойственна f*, – это так называемое свойство взаимности.
Пусть формула U реализует функцию f(x1,x2,…,xn). Найдем формулу, реализующую двойственную функцию f*(x1,x2,…,xn).
-
О двойственной функции
Пусть функция Ф(x1,x2,…,xn) является суперпозицией функций f1(x11,x12,…,x1p1), f2(x21,x22,…,x2p2),…, fs(xs1,xs2,…,xsps), т.е. Ф(x1,x2,…,xn)=f(f1(x11,x12,…,x1p1), f2(x21,x22,…,x2p2),…, fs(xs1,xs2,…,xsps)), где x1,x2,…,xn – это все различные символы имен переменных из наборов (x11,x12,…,x1p1), (x21,x22,…,x2p2), …,(xs1,xs2,…,xsps), тогда Ф*(x1,x2,…,xn)=f*(f*1(x11,x12,…,x1p1), f*2(x21,x22,…,x2p2),…, f*s(xs1,xs2,…,xsps)).
Доказательство:
По определению
двойственной функции Ф*(x1,x2,…,xn)=
=
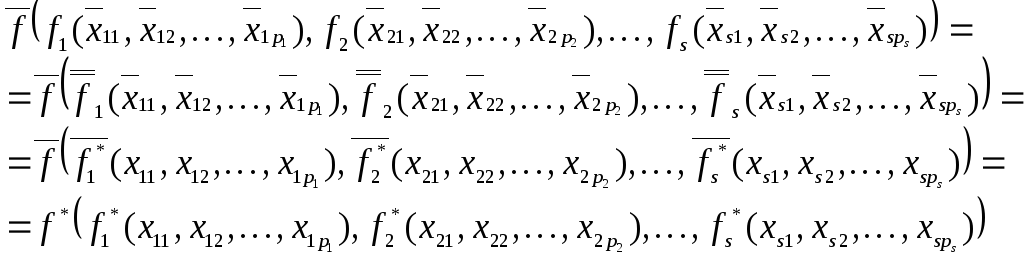
Из этой теоремы следует так называемый принцип двойственности:
Пусть формула U=S [f1, f2,…, fp] реализует функцию f(x1,x2,…,xn), тогда формула S [f1*, f2*,…, fp*], полученная из формулы U заменой функций f1, f2,…, fp двойственными функциями f1*, f2*,…, fp* соответственно, реализует функцию f*(x1,x2,…,xn), двойственную f. Эта формула называется двойственной к формуле U и обозначается U*. Таким образом, U*= S [f1*, f2*,…, fp*], где S означает структуру формулы. Заметим, что структура формулы, определяемая порядком выполняемых действий, остается неизменной.
На практике наиболее часто принцип двойственности применяется к формулам, сконструированным из таких функций, как константы ноль и единица, тождественной функции, отрицания, конъюнкции и дизъюнкции. В таких случаях для получения двойственной формулы необходимо ноль заменить на единицу, а единицу на ноль везде, где они встречаются, знак «&» заменить знаком «», а знак «» – на «&». При этом следует учесть порядок выполняемых действий в исходной формуле и, если он не был задан явно скобками, а задавался только приоритетом операций, то, возможно, придется расставить скобки в двойственной формуле. Тогда установить их надо на тех же местах, где они неявно присутствовали в исходной формуле. В других случаях, ввиду того же старшинства операций, в двойственной формуле скобки, возможно, и не понадобятся.
Примеры:
U1(x,y) = x & y U1*(x,y) = x y;
U2(x,y) = x & y 
U2*(x,y) = (x y) &
;
U3(x,y) = (x y) & (
)
U3*(x,y) = x & y 
.