17 Обобщенный закон Гука

Обобщенный закон Гука представляет собой связь между напряжениями и деформациями в случае объемного, и как частый случай, плоского напряженных состояний.

Он может быть получен на основании з-на Гука для линейного напряжен состояния и принципа независимости действия сил.

Пусть задано произвольное объемное напряж состояние с главными напряжениями ,  и . Представим его в виде суммы 3х линейных напряженных состояний. Учитывая, что при линейном напряженном состоянии  и  запишем выражение для лин относит деформации в направлении :

      Деформации в направлении действия главных напряжений равны

       ,

        ,

         .

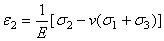Эти выражения носят название обобщенного закона Гука, записанного для главных площадок. Деформации , , , в направлении главных напряжений называются главными деформациями.

Соотношения обобщенного закона Гука могут быть записаны для любых (не главных) площадок, но т.к. при этом будут действовать, кроме нормальных и касательные напряжения (рис.3.10), то необходимо добавить три соотношения для вычисления угловых деформаций. Таким образом, для произвольных площадок обобщенный закон Гука содержит 6 соотношений, связывающих деформации и напряжения:

,

,

,

;      ;      .

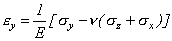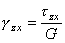18 Температурные напряжения. Методика решения.

Вторым важным свойством статически неопределимых систем является то, что при изменении температурных условий работы конструкций в элементах возникают напряжения, которые называются температурными напряжениями. Это обстоятельство следует учитывать на стадии проектирования конструкций, т.к. температурные напряжения, суммируясь алгебраически с рабочими напряжениями, могут привести материал к предельному состоянию (текучести или хрупкому разрушению).

Расчёт температурных напряжений для стержня, уложенного с зазором между двумя жёсткими плитами, рассмотрен на примере в конце данного раздела. Определим температурные напряжения в шарнирно- стержневой системе.

Пример

Решение

Статическая сторона задачи:

Предположим, что во всех стержнях возникают растягивающие продольные усилия (дальнейшее решение уточнит правильное направление усилий):

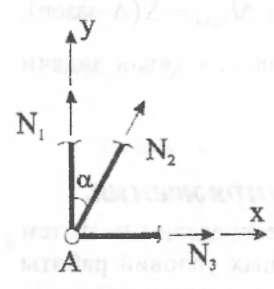
Равновесие узла А:

Анализ полученных результатов показывает, что все три стержня унеличивают свою длину, что полностью соответствует деформационной схеме. Несмотря на то, что в стержнях 1 и 3 возникает сжимающая продольная сила, деформация укорочения, которую она вызывает, незначительна по сравнению с удлинением стержня от нагрева.

Изменение температурных условий работы конструкции опасно не столько из-за появления температурных напряжений, сколько из-за нозникновения больших удлинений или укорочений элементов. И эта опасность, главным образом, относится к хрупким материалам, которые разрушаются при малых деформациях. Для пластичных материалов температурные напряжения не столь опасны, в крайнем случае они могут привести к незначительным остаточным деформациям.