Графики

Используя данные корреляционной таблицы, построим гистограммы, полигоны и графики эмпирических функций распределения для X и Y (рис. 2 — рис. 11):

Рис. 2. Гистограмма частот случайной величины X

Рис. 3. Полигон частот случайной величины X

Рис. 4. Гистограмма нормированных относительных частот случайной величины X

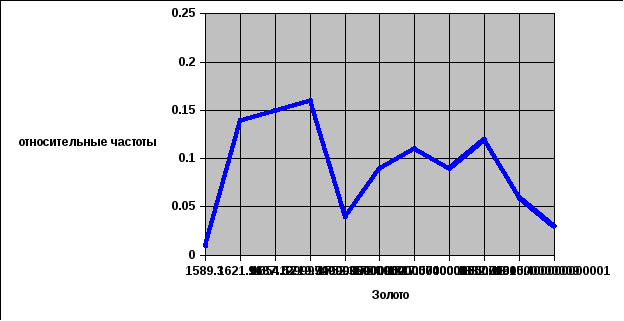
Рис. 5. Полигон относительных частот случайной величины X

Рис. 6. Эмпирическая функция распределения случайной величины X

Рис. 7. Гистограмма частот случайной величины Y

Рис. 8. Полигон частот случайной величины Y

Рис. 9. Гистограмма относительных нормированных частот случайной величины Y

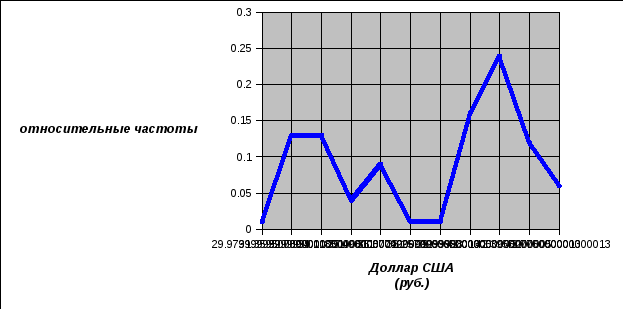
Рис. 10. Полигон относительных частот случайной величины Y

Рис. 11. Эмпирическая функция распределения случайной величины Y

Линейная регрессия

Метод нахождения минимального отклонения и есть метод наименьших квадратов.

.

Это суммарное отклонение зависит от коэффициентов а и b функции Y, поэтому эти коэффициенты должны быть минимальными, то есть производная функции в этих точках равны нулю:

Найдя частные производные и приравняв их нулю, получим следующую систему уравнений:

Решив эту систему, мы найдем наилучший набор этих параметров. Эта теоретическая кривая с параметрами, которые определяются методом наименьших квадратов, и будет искомой линией — линией линейной регрессии.

Для нахождения коэффициентов a и b методом наименьших квадратов были посчитаны следующие необходимые параметры:

= 298048622,6;

= 172403,3;

= 6436897,193;

= 3720,815.

Решив данную систему уравнений методом Гаусса, мы получим значения коэффециентов a и b.

В нашем случае коэффициенты а и b соответственно равны:

; .

Следовательно, уравнение линейной регрессии для нашей выборки (рис. 12) имеет вид:

y = 0,0269x - 9,2544

Рис. 12. Линейная регрессия y по x

Выразим уравнение линейной регрессии X по Y, тогда уравнений будет иметь вид:

Подставим значения и получим:

Упростим и получим уравнение:

x = 11,84y + 1283,5

Таким образом, коэффициент a=-11,84, b=1283,5.

Параболическая регрессия

Уравнение регрессии в форме параболы второго порядка имеет вид: . Суммарное отклонение зависит от коэффициентов , и этой функции. Как и в предыдущем исследовании, нам необходимо провести оптимальную кривую, т. е. найти минимум функции .

Известно, что минимум достигается в точках, где частные производные равны нулю. В нашем случае имеем:

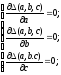
В итоге получаем следующую систему уравнений, откуда находим коэффициенты a, b и c:

Для нахождения коэффициентов a, b и c методом наименьших квадратов были посчитаны следующие необходимые параметры:

89821137170;

5,16691;

= 298048622,6;

1116761,858;

= 172403,3;

= 6436897,193;

= 3720,815.

Получаем систему уравнений:

Данную систему уравнений мы решаем методом Крамера, для чего вычислим соответствующие определители:

В нашем случае коэффициенты а, b и c соответственно равны: , , .

Следовательно, уравнение параболической регрессии для нашей выборки (рис. 14) имеет вид:

y = 0,0002x² - 0,7591x + 670,97

Рис. 14. Параболическая регрессия