Фізичний зміст шпф

Нехай є функція x = sin(t), максимальна амплітуда коливання якої дорівнює 1(див. рис.А1).

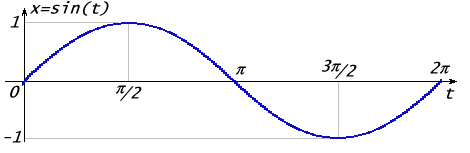
Рис.А.1

Якщо помножити значення синуса на деякий коефіцієнт A, то одержимо графік, розтягнутий по вертикалі в A раз: x = Asin(t). Період коливання дорівнює 2π. Якщо необхідно збільшити період до T, то треба помножити змінну t на коефіцієнт, що викличе розтягання графіка по горизонталі: x = A sin(2πt/T).

Частота коливання обернена періоду: ν = 1/T. Кругова частота обчислюється за формулою: ω= 2πν = 2πT. Звідки: x = A sin(ωt). Фаза (φ) визначає зсув графіка коливання вліво. У результаті сполучення всіх цих параметрів отримується гармонійне коливання або просто гармоніку (див. рис.А2):

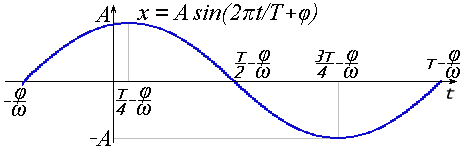
Рис.А2.

При зміні фази на π/2 отримується вираження гармоніки через косинус (див. рис. А3):

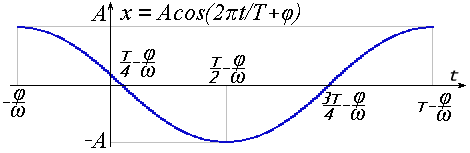
Рис.А3.

x = A cos(2πt/T + φ) = A cos(2πνt + φ) = A cos(ωt + φ) (А1)

Подібною функцією описуються коливання маятника, струни, водні і звукові хвилі тощо.

Перетворимо (А1) за формулою косинуса суми:

x = A cos φ cos(2πt/T) - A sin φ sin(2πt/T) (А2)

Виділимо в (А2) елементи, незалежні від t, і позначимо їх як Re і Im:

x = Re cos(2πt/T) - Im sin(2πt / T) (А3)

Re = A cos φ, Im = A sin φ

За величинами Re і Im можна однозначно відновити амплітуду і фазу вихідної гармоніки:

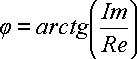   і    (А4)

Виконаємо над формулою(2) такі дії: розкладемо кожне комплексне X_k на уявну і дійсну складові X_k = Re_k + j Im_k; розкладемо експоненту за формулою Ейлера на синус і косинус дійсного аргументу; перемножимо; внесемо 1/N під знак суми і перегрупуємо елементи у дві суми:

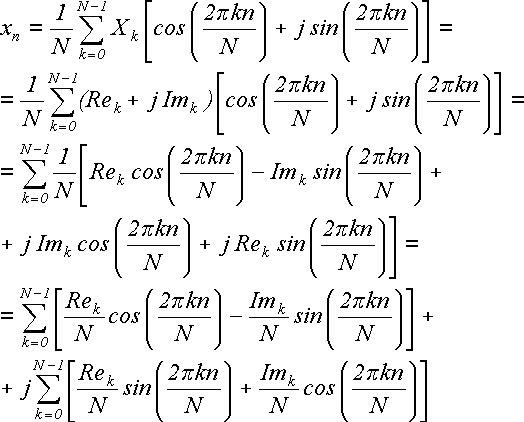    (А5)

Для аналізу формули (А5) розглянемо приклад. Нехай маємо є звукове коливання у вигляді функції x = f(t), яке представлене у вигляді графіка для відрізка часу [0, T] (див.рис.А4). При дискретизації відрізок ділиться на N-1 частин і визначаються значення функції x₀, x₁, x₂,..., x_N для N крапок на границях відрізків t₀ = 0, t₁ = T/N, t₂ = 2T/N,..., t_n =n/N,..., t = T.

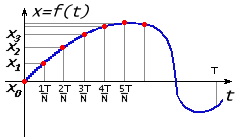
Рис.А4

У результаті прямого ДПФ (1) отримані N значень для X_k. Тепер при застосуванні зворотне ДПФ отримаємо вихідну послідовність {x}, яка складалася з дійсних чисел (послідовність {X} у загальному випадку комплексна).

У формулі (А5) ліворуч стоїть дійсне число x_n, а праворуч - дві суми, одна з яких помножена на j. Самі ж суми складаються з дійсних доданків. Звідси виходить, що друга сума дорівнює нулю при дійсному значенні вихідної послідовності {x}. При її відкиданні отримується (16):

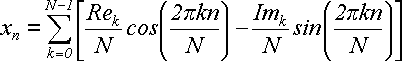(А6)

Оскільки при дискретизації t_n = nT/N і x_n = f(t_n), то можна виконати заміну: n = t_nN/T. Отже, у синусі і косинусі замість 2πkn/N можна написати 2πkt_n/T. У результаті отримаємо (17):

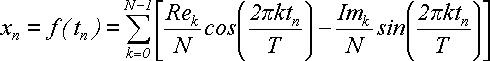(А7)

На основі аналізу формул (А1), (А3) і (А7), видно, що остання формула є сумою з N гармонійних коливань різної частоти, фази і амплітуди 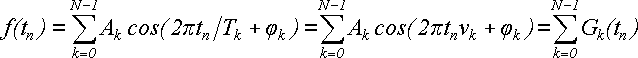(А8):

(А8)

А функція називається k-ою гармонікою.

G_k(t) = A_k cos(2πtk/T + φ_k) (А9)

Отже, амплітуда, фаза, частота і період кожної з гармонік пов'язані з коефіцієнтами X_k формулами 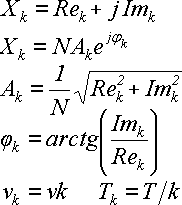(А10):

(А10)

Фізичний зміст дискретного перетворення Фур'є полягає в представленні дискретного сигналу у вигляді суми гармонік. Параметри кожної гармоніки обчислюються прямим перетворенням, а сума гармонік - зворотним.

4