§1 Применение функций в экономике

Функции находят широкое применение в экономической теории и практике. Спектр использования разнообразных функций: от простейших линейных до функций, полученных по определённому алгоритму с помощью программ, рекуррентных соотношений, связывающих состояния изучаемых объектов в разные периоды времени. На ряду с линейными используются нелинейные монотонные функции, моделирующие характер тенденции экономического процесса (возрастания, убывания, и т.д.). Периодичность экономического процесса позволяет учесть тригонометрические модели.

Часто в экономическом процессе удаётся выделить основной фактор, определяющий тип тенденции, а действием побочных факторов пренебречь (или зафиксировать побочные факторы на одном уровне), тогда влияние основного фактора изучается с помощью функции одной переменной , где x - независимая (факторная) переменная, y - зависимая (результативная) переменная. y

Пример 1. Зависимость спроса y на разные товары от дохода x описывается функциями Л. Торнквиста: , , , где а1, а2, а3 – уровни дохода, при которых начинается потребление тех или иных товаров; b1, b2 – уровни насыщения для групп товаров первой и второй необходимости.	b2 b1 0 а1 а2 а3 x
Пример 2. Рассматривая в одной системе координат кривую спроса и кривую предложения, можно установить равновесную точку p0 - рыночную цену товара, формируемую в условиях конкурентного рынка.	кривая кривая спроса предложения p0
Пример 3. Пусть - функция издержек (полных затрат) фирмы; - функция дохода от объёма производства q. Тогда прибыль при данном производстве составляет . И можно установить уровни объёма производства, при которых это производство приносит прибыль , , или же производство убыточно , или даёт максимальную прибыль или максимальный убыток и найти их размеры.	у 0 q1 q2 q3 q4

§2 Классификация тенденций экономических процессов

При решении задач экономики часто необходимо анализировать тенденции экономических показателей. Рассмотрим разные варианты изменения переменной у при увеличении факторной переменной х с учетом двух признаков: направления изменения величины и направления изменения предельной величины зависимой переменной . y

I Тенденция возрастания с постоянной скоростью может быть описана линейным уравнением или , . Тогда скорость возрастания y равна - постоянна и неотрицательна.

k b x x

Пример 1 Стоимость покупки возрастает с постоянной скоростью k (цена продукта) по мере увеличения веса х покупаемого продукта.

Пример 2 Если затраты от реализации единицы товара постоянны и не зависят от объема реализации x, то совокупные издержки и суммируются из kx - издержек от реализации товара в объеме x и b - постоянных издержек.

II Тенденции возрастания с постоянно убывающей скоростью описывается выпуклой вверх возрастающей кривой , которая либо , либо . При этом производная монотонно убывает с ростом x.

у А х х х

Математические модели: (, ) – степенная модель, () – логарифмическая модель, - дробно-рациональная модель.

Пример 1 Закон убывающей предельной полезности (Д. Бернулли 1788 г.): совокупная полезность U с ростом объема x потребляемого блага возрастает с монотонно убывающей скоростью.

Пример 2 Закон убывающей доходности ресурсов: по мере увеличения количества используемого в производстве переменного ресурса k при неизменном уровне других фиксированных ресурсов неизбежно наступает момент, когда по мере увеличения k прирост продукции , приходящийся на очередную порцию используемого ресурса будет монотонно снижаться.

III Тенденция возрастания с монотонно возрастающей скоростью описывается вогнутой возрастающей кривой , при этом . Математические модели: - полиномиальная,

у х х

(, ) – степенная, (, ) – экспоненциальная. Особенность экспоненциальной модели в следующем: - не зависит от аргумента х. Отношение называют темпом роста.

П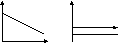ример Закон спроса: в условиях монопольного рынка при увеличении объема продаж х совокупная выручка W возрастает с монотонно возрастающей скоростью. y

IV Тенденция убывания с постоянной скоростью может быть описана линейным уравнением или , , . Тогда скорость возрастания y равна - неотрицательная постоянная.

b k x

Пример 1 Закон спроса: спрос D на товар линейно падает с ростом цены р на этот товар.

Пример 2 Линейная модель амортизации: текущая стоимость у средств производства линейно убывает с ростом срока х эксплуатации средств производства , где b - исходная стоимость средств производства.

V Тенденция убывания с монотонно убывающей скоростью описывается убывающей вогнутой кривой, имеющей горизонтальную асимптоту , . монотонно убывает по абсолютной величине с ростом х. Математические модели: (, ) – степенная модель,

у х х

(, ) – экспоненциальная модель с постоянным темпом , (,, ) – экспоненциальная модель с горизонтальной асимптотой, (, ) - дробно-рациональная модель.

Пример 1 Закон убывающей предельной полезности: предельная полезность (полезность последней порции потребленного блага) монотонно убывает с ростом общего объема х потребленного блага.

Пример 2. Спрос D на товар монотонно падает с ростом цены р.

Пример 3. Всякая система (коллектив, организм, устройство и т.п.) при заданных условиях деятельности имеет определенную продуктивность (производительность) П. Воздействие на систему с целью повышения её продуктивности называется стимуляцией системы. Принцип убывающей отдачи А.Тюрго-Т.Мальтуса гласит: чем выше текущая продуктивность системы П, тем меньше окажется прирост её продуктивности за счет воздействия очередной порции стимулятора. Например, размер оплаты труда стимулирует рост производительности работника П до определенного предела. По мере увеличения зарплаты (интенсивности труда П), стимулирующей эффект от очередной надбавки к зарплате неуклонно снижается.

VI Тенденция убывания с монотонно возрастающей скоростью описывается выпуклой убывающей кривой y=f(x), производная которой отрицательна и монотонно возрастает по абсолютной величине. В чистом виде такая тенденция встречается редко. Наблюдается в составных моделях.

у х х