
- •Оглавление
- •Глава 1 интегрирование функций комплексного переменного
- •1.1. Основные понятия. Формы записи. Геометрическая интерпретация. Свойства
- •Теорема Коши для односвязной области
- •Теорема Морера
- •Теорема Коши для −связной области
- •Доказательство
- •Следствия теоремы Коши для −связной области
- •Интегральная формула Коши
- •Следствие интегральной формулы Коши
- •1.4. Задачи для самостоятельной работы (по главе 1)
- •Глава 2 Ряды в комплексной области.
- •2.1. Числовые ряды. Основные понятия
- •2.2. Функциональные ряды. Область сходимости. Равномерная сходимость. Свойства. Степенные ряды с комплексными членами
- •Свойства равномерно сходящихся рядов
- •Признак Вейерштрасса (достаточный признак равномерной сходимости)
- •Теорема Абеля
- •2.3. Ряды Тейлора Теорема
- •Основные разложения
- •2.4. Задачи для самостоятельной работы (по главе 2)
- •Библиографический список
- •Часть II
Свойства равномерно сходящихся рядов
Равномерно
сходящиеся ряды от непрерывных функций
комплексного переменного на множестве
![]() обладают свойствами конечных сумм:
обладают свойствами конечных сумм:
1) сумма ряда
![]() является непрерывной функцией на
множестве
является непрерывной функцией на
множестве ![]() ;
;
2) ряд можно почленно интегрировать;
3) ряд, составленный из аналитических функций можно почленно дифференцировать.
Признак Вейерштрасса (достаточный признак равномерной сходимости)
Если
ряд
![]() на некотором множестве
на некотором множестве
![]() мажорируется сходящимся числовым рядом
мажорируется сходящимся числовым рядом
![]() с положительными членами
с положительными членами
![]() ,
то он сходится на области
,
то он сходится на области
![]() равномерно.
равномерно.
Ряд вида
![]() =
=![]() ,
(24)
,
(24)
где ![]() − комплексная
переменная;
− комплексная
переменная; ![]() − комплексные
числа, является степенным
рядом в
комплексной области.
− комплексные
числа, является степенным
рядом в
комплексной области.
При
![]() степенной ряд принимает вид
степенной ряд принимает вид
![]() =
=![]() .
(25)
.
(25)
для исследования сходимости степенных и функциональных рядов остаются справедливыми основные положения, известные из действительного анализа.
Теорема Абеля
Если
степенной ряд
![]() сходится в некоторой точке
сходится в некоторой точке
![]() ,
то он абсолютно сходится в круге
,
то он абсолютно сходится в круге
![]() .
.
Если ряд
![]() расходится в точке
расходится в точке
![]() ,
то он расходится и при любом значении
,
то он расходится и при любом значении
![]() ,
для которого
,
для которого
![]() .
.
Число
![]() называют радиусом
сходимости
степенного ряда
называют радиусом
сходимости
степенного ряда
![]() ,
область
,
область
![]() − кругом сходимости ряда. Для степенного
ряда
− кругом сходимости ряда. Для степенного
ряда
![]() областью сходимости будет круг
областью сходимости будет круг
![]() .
.
Радиус сходимости находят по уже известным из действительного анализа формулам:
![]() (26)
(26)
или ![]() (27)
(27)
Для рядов вида
![]() радиус сходимости находят по тем же
формулам, но для
радиус сходимости находят по тем же
формулам, но для
![]() .
.
Исследование сходимости ряда можно также провести, применяя непосредственно признаки сходимости.
Границу области сходимости необходимо исследовать дополнительно. На границе круга сходимости могут лежать как точки сходимости, так и точки расходимости степенного ряда.
Задача 18.
Найти область сходимости ряда
![]() .
.
Решение
Исследуют ряд непосредственно по признаку Даламбера:
![]() ,
где
,
где ![]() .
.
![]() .
.
Получают, что при
![]() область сходимости вырождается в точку.
область сходимости вырождается в точку.
При
![]() ряд расходится.
ряд расходится.
Задача 19. Найти
радиус сходимости ряда
![]() .
.
Решение
Находят значение радиуса сходимости по формуле (26), учитывая, что
![]() .
.
![]() Ряд
сходится в круге
Ряд
сходится в круге
![]()
Задача 20. Найти
круг сходимости степенного ряда
![]() .
.
Решение
Находят значение
![]() по формуле (27):
по формуле (27):
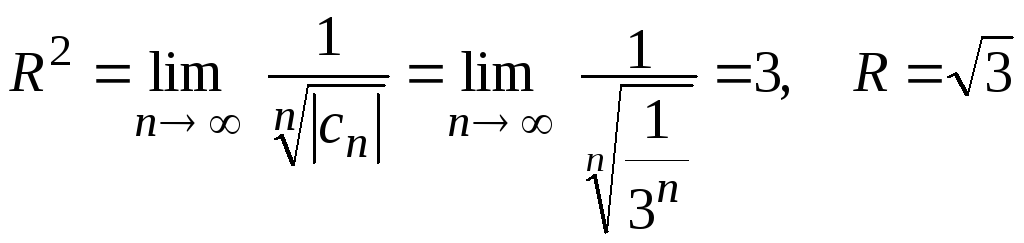 .
.
Ряд сходится, если
![]() .
.
На границе
![]() получают ряд
получают ряд
![]() ,
который расходится, так как не выполняется
необходимый признак. Окончательно
получают, что область сходимости – круг
,
который расходится, так как не выполняется
необходимый признак. Окончательно
получают, что область сходимости – круг
![]()
Задача 21. Исследовать ряд ![]() на абсолютную и
равномерную сходимость.
на абсолютную и
равномерную сходимость.
Решение
Находят значение радиуса сходимости по формуле (26):
![]() .
.
Ряд сходится в
круге
![]() .
На границе круга
.
На границе круга
![]()
![]() получают
ряд
получают
ряд
![]() ,
,
который не является знакоположительным.
Для исходного ряда составляют ряд из модулей его членов:
![]() .
.
Полученный ряд сходится.
Следовательно, и
исходный ряд ![]() сходится в замкнутом круге
сходится в замкнутом круге
![]() ,
причем абсолютно.
,
причем абсолютно.
Так как в этом круге исходный ряд мажорируется сходящимся числовым рядом, то по признаку Вейерштрасса сходимость в этом замкнутом круге будет равномерная.
Задача 22. Исследовать
сходимость степенного ряда
![]() .
.
Решение
Находят значение радиуса сходимости по формуле (26):
![]() .
.
Область сходимости
данного ряда − круг с центром в точке
![]() и радиусом
и радиусом
![]() ,
т.е. вся комплексная плоскость.
,
т.е. вся комплексная плоскость.
Задача 23. Исследовать
на равномерную сходимость ряд
![]() .
.
Решение
Для равномерной
сходимости исходный ряд должен
мажорироваться сходящимся числовым
рядом ![]() .
.
Полученный числовой
ряд
![]() сходится при условии
сходится при условии
![]() или
или
![]() ,
, ![]() .
Следовательно, исходный ряд
.
Следовательно, исходный ряд
![]() равномерно сходится в области
равномерно сходится в области
![]() .
.
Задача 24. Найти сумму ряда
а)![]() ; б)
; б)
![]() .
.
Решение
а) Данный ряд
имеет вид
![]() и сходится при
и сходится при
![]() ,
в круге
,
в круге
![]() .
.
Последовательность частичных сумм
![]()
находят по формуле суммы членов геометрической прогрессии
![]() .
.
При
![]() для членов бесконечной убывающей
прогрессии получают сумму ряда
для членов бесконечной убывающей
прогрессии получают сумму ряда ![]() =
= .
.
б) Для
решения этой задачи используют свойство
дифференцирования ряда
![]() .
При дифференцировании получают
.
При дифференцировании получают
![]() или
или
![]() .
.
Окончательно
находят
![]() .
сумма
ряда будет
.
сумма
ряда будет
![]() при
при
![]() .
.
