Следствие интегральной формулы Коши
Если функция
− аналитическая функция в замкнутой
области
и имеет производные всех порядков, то
данные производные можно получить по
следующей формуле Коши:
(19)
Используется для вычисления контурных интегралов вида
.
Направление
интегрирования в формулах (18)–(19)
считается положительным,
−
любая внутренняя точка области
,
ограниченная контуром
.
Задача 10.
Вычислить
интеграл
,
где контур
задан следующими вариантами:
а)
; б)
; в)
; г)
.
Решение
а)
− особые точки функции
=
.
Все точки лежат
вне контура
(см. рис. 9). Следовательно, внутри
области, ограниченной этим контуром,
подынтегральная функция является
аналитической.
По теореме Коши для односвязной области (16)
= 0.
б) Внутрь контура
попадает одна точка
(см. рис. 10).
Используют
интегральную формулу Коши. Преобразуют
подынтегральное выражение. функция
является аналитической в круге
.
по
формуле (18) для функции
и точки
в) Внутрь
контура
попадает одна точка
(см. рис. 11). Используют интегральную
формулу Коши. Преобразуют подынтегральное
выражение.
Функция, выделенная в числителе, является аналитической в рассматриваемой области.
Тогда по формуле (18) получают
г) Внутрь контура
попадают две точки
и
(см. рис. 12).
особые
точки ограничивают окружностями
достаточно малых радиусов −
и
с центрами в этих точках так, чтобы они
не пересекались и целиком лежали внутри
контура
.
В трехсвязной
области, ограниченной контурами
,
и
подынтегральная функция является
аналитической.
По теореме Коши
для
-связной
области получают
=
Задача 11.
Вычислить
интеграл
.
Решение
Для функции
точка
− особая точка. Она является кратной и
попадает внутрь контура
.
Используют следствие интегральной
формулы Коши (для
,
).
Функция
− аналитическая в области
.
Преобразуют подынтегральное выражение по формуле (19):
.
Задача 12.
Вычислить
интеграл
.
Решение
функция
имеет две особые точки
и
,
лежащие внутри круга
.
Дробь
раскладывают на простейшие дроби: 
.
По известному
правилу находят 
По формулам (18) - (19) окончательно получают
=
Задача 13.
Вычислить
интеграл
.
Решение
В контур
попадает только
одна особая точка
.
Преобразуют подынтегральное выражение
По формуле (18) окончательно получают
.
1.4. Задачи для самостоятельной работы (по главе 1)
1. Вычислить следующие интегралы:
, 
,
где L
− соединяет точки
:
а) по прямой;
б) по параболе;
в) по ломаной, состоящей из отрезков параллельных координатным осям.
Сравнить полученные результаты.
2. Вычислить 
а) по прямой L,
соединяющей точки
;
б) по прямой L,
соединяющей точки
;
в) по параболе,
соединяющей точки
.
3. Вычислить
а) по радиус-вектору
точки
;
б) по верхней
полуокружности
из точки
;
в) по окружности
с центром в точке
и радиусом
;
г) по дуге параболы
,
соединяющей точки
;
д) по дуге гиперболы,
соединяющей точки
;
е) по прямой,
соединяющей точки
.
4. Вычислить
,
L: 
,
нижняя часть.
5. Вычислить
,
L: 
(обход против часовой стрелки).
6. Вычислить
по прямой L,
соединяющей точки
.
7. Вычислить
,
L: 
(обход против часовой стрелки).
8. Вычислить
,
L: 
.
9. Вычислить
,
L: ломаная,
состоящая из отрезков, параллельных
координатным осям через точки
.
10.
по прямой L,
соединяющей точки
.
Изменится ли значение интеграла, если изменить кривую через эти точки?
11. Вычислить
по прямой L,
соединяющей точки
.
12. Вычислить
,
L: 
, (
).
13. 
по прямой L,
соединяющей точки
.
14. 
по прямой L,
соединяющей точки
.
15. Вычислить
,
где L:
а)
,
нижняя часть (обход против часовой
стрелки);
б)
,
правая часть (обход против часовой
стрелки);
в) отрезок прямой,
соединяющей точки
.
16. Вычислить:
а) 
; г) 
;
б) 
; д) 
,
в) 
; е) 
.
17. Вычислить
вдоль любых кривых, где функция
непрерывна. Сравнить полученные
результаты.
18. Вычислить:
а) 
; б) 
.
19. Вычислить:
а)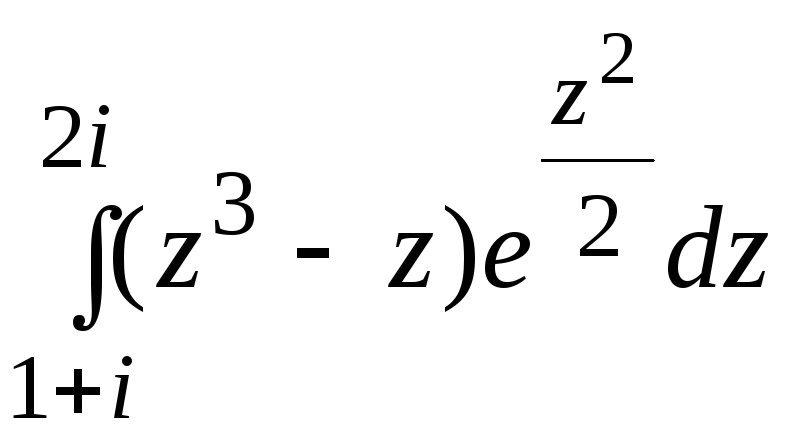 
; б) 
.
20. Вычислить
по прямой L,
соединяющей точки
.
21. Вычислить
,
L: 
,
первая четверть.
22. Вычислить
.
23. Вычислить
а) по прямой,
соединяющей точки
;
б) по ломаной с
вершинами в точках
.
Вычислить следующие интегралы:
24. 
, где
− окружность:
а) 
; б) 
; в) 
.
25. 
, где
− окружность
.
26. 
, где
− окружность:
а) 
; б) 
; в) 
.
27. 
,
где
− окружность:
а) 
; б) 
; в) 
.
28. 
,
где
− окружность:
а) 
; б) 
.
29.
, где
− окружность 
.
30. 
, где
− окружность 
.
31. 
, где
− окружность 
.
32. 
, где
− эллипс
33. 
, где
− окружность 
.
34. 
, где
− окружность 
.
35. 
, где
− окружность 
.
36. 
,
где
− окружность 
.
37. 
, где
− окружность:
а) 
; б) 
; в) 
.
38.
.
Провести исследование для различных контуров интегрирования:
а)
;
б)
;
в)
;
г)
.
Какие из этих интегралов равны нулю?
39. Пусть известно,
что
.
следует
ли тогда, что
является
аналитической в области
,
ограниченной контуром С?