Метрология.

8.09.10 Истинное значение измеряемой величины.

Целью каждого измерения является определение некоторой величины, но из-за различных неточностей исходной постановки задачи и погрешностей результаты могут быть различны.

Методологическая схема измерений

Ɛ(внешние факторы)

Объект измерений

Измерительная система(устройства)

Результат

На сегодняшний день совместно с метрологией работают:

1. Теория планирования измерений.

2. Теория интерпретации измерений.

Прямые –измерения являются прямыми, если конечный результат получается без преобразований исходной измерительной информации.

Косвенные – измерения, конечный результат которых получаем входе преобразования исходной измерительной информации.

Совокупные –измерения, результаты которых состоят как из прямых так и из косвенных результатов.

Общая классификация измерений.

Измерения:

1)По зависимости от времени ( статические и динамические).

2) По характеру точности (равноточные и Неравноточные).

3) По числу измерений (однократные и многократные).

4) По способу выражения результатов (абсолютные и относительные).

5) По способу получения результатов (прямые, косвенные и совокупные).

15.09.10 Структура погрешностей измерений.

Погрешность измерений:

1. Систематическая :

- по характеру появления:

1.простая

2.переменная (прогрессивная, периодическая и изменяемая по сложному закону)

- по причине появления:

1.методическая

2.инструменталь (не совершенность конструкции, не совершенность технологий и износ и старение материала)

3.погрешность установки

4.влияющая величина

5.субъективность

2)Случайная.

3)Грубая (аномальная).

Qизм –измеренное значение измеряемой величины.

Замечание: в (1) случай аддитивной погрешности измерения.

Замечание: во (2) случай мультипликативная погрешности измерения.

Погрешность зависит от применяемого метода измерений и применяемой аппаратуры. Одной из основных задач является учет или исключение причин возникновения погрешностей.

Функции распределения результатов и погрешностей измерений.

График1:

Наиболее полным описанием некоторых случайных величин является знание функции F(x) распределения этой величины.

1. 

F(x) = вероятность(1)

2. Функция плотности вероятности.

(2) =>

Основные свойства функций F(x) иf(x).

Графики 2:

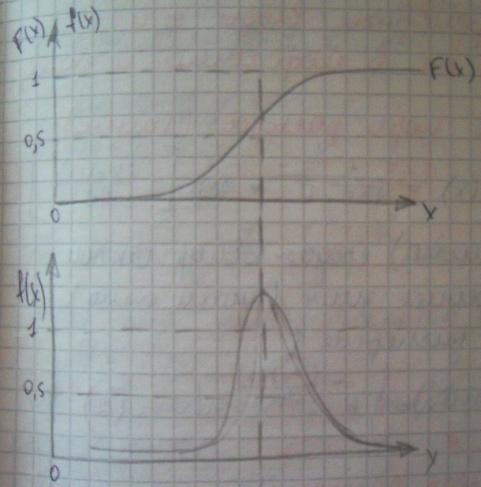
1)вероятность не может быть отрицательной.

2)

3)

4)

Эти свойства характерны для всех видов функций вероятности.

Основные виды функций вероятности в метрологии и стандартизации.

Функция нормального распределения(Гаусса).

(1)

– среднее значение( математическое ожидание)

– среднее квадратичное отклонение.

– дисперсия

Интеграл Лапласа:

(2)

Можно посчитать с помощью компонента и математической таблицы.

Функция является параметрической.

22.09.10 Стандартная( приведенная) функция нормального распределения (или функция Гаусса)

(1)

(2)

Есть еще общепринятое обозначение:

Ф= F(x)

В общем случае переход от стандартной функции:

Функция равномерного распределения

а) , где х – погрешность\ сам результат

Графики 3:

дифференциальная функция

интегральная функция

Погрешность измерений во всем диапазоне будет одинаковым.

б) Графики 4:

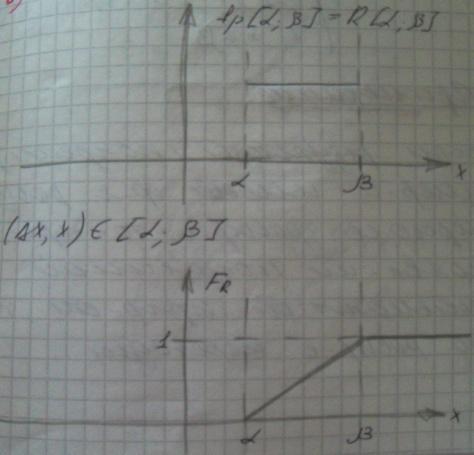
Fr- функция равномерного распределения

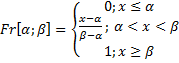
Примечание: если результаты( погрешности) измерений имеет функция равномерного распределения, то при появлении постоянной систематической погрешности, то это распределение переходит.

Треугольное распределение

Графики 5:

Закон Релея.

Связан с круговой системой координат.

График 6:

Замечание:

При выводе закона предполагаем, что функция распределения координат имеет нормальное распределение.

fp(r) - Функция релейного распределения.

График 7:

Для функции распределения Релея среднее значение:

M[r] - Математическое ожидание.

Разброс радиуса меньше разброса любой из координат.

График 8:

Экспоненциальные распределения.

Fe- Функция вероятности.

Графики 9:

Интенсивность того или другого процесса

90% всех процессов идет по экспоненциальному закону(например: лавина)

В метрологии при измерении погрешностей.