
- •Часть II.
- •Исследование электрического поля проводника с током
- •Порядок выполнения работы
- •Теоретическая часть
- •Контрольные вопросы
- •Литература
- •Измерение сопротивлений проводников мостовыми схемами
- •Описание установки
- •Порядок выполнения работы
- •Теоретическое описание
- •Контрольные вопросы
- •Литература
- •Релаксационные колебания
- •Порядок выполнения работы
- •Теоретическое описание
- •Контрольные вопросы
- •Литература
- •Термоэлектрические явления
- •Установки
- •Теоретическое описание
- •Я Рис.9 вление Зеебека.
- •Контрольные вопросы
- •Литература
- •Определение удельного заряда электрона методом магнетрона
- •Теоретическое описание
- •Контрольные вопросы
- •Литература
- •Магнитное поле земли
- •Порядок выполнения работы
- •Теоретическое описание
- •Метод тангенс-гальванометра
- •Закон Био-Савара-Лапласа
- •Контрольные вопросы
- •Литература
- •Исследование магнитного поля соленоида
- •Порядок выполнения работы
- •Теоретическое описание
- •Теорема о циркуляции
- •Закон Био-Савара-Лапласа
- •Контрольные вопросы
- •Литература
- •Определение индуктивности тороида с ферритовым магнитопроводом
- •Порядок выполнения работы
- •Теоретическое описание
- •Теорема о циркуляции
- •Контрольные вопросы
- •Литература
- •Исследование электрических затухающих колебаний
- •Описание лабораторной установки
- •Порядок выполнения работы.
- •Теоретическая справка:
- •Контрольные вопросы.
- •Литература.
- •Определение основных характеристик электрического колебательного контура методом резонанса
- •Описание установки.
- •Порядок выполнения работы.
- •Теоретическое описание.
- •Контрольные вопросы.
- •Литература
Теоретическое описание
Рис.1
![]() имеется в случае бесконечно длинного
соленоида - цилиндрической катушки, по
виткам которой протекает электрический
ток. Опыт показывает, что чем длиннее
соленоид, тем меньше индукция магнитного
поля вне его. Для бесконечно длинного
соленоида магнитное поле снаружи
отсутствует вообще, а внутри его линии
вектора
имеется в случае бесконечно длинного
соленоида - цилиндрической катушки, по
виткам которой протекает электрический
ток. Опыт показывает, что чем длиннее
соленоид, тем меньше индукция магнитного
поля вне его. Для бесконечно длинного
соленоида магнитное поле снаружи
отсутствует вообще, а внутри его линии
вектора
![]() направлены вдоль его оси, причем вектор
направлены вдоль его оси, причем вектор
![]() составляет с направлением тока в
соленоиде правовинтовую систему (рис.1).
составляет с направлением тока в
соленоиде правовинтовую систему (рис.1).
Из теоремы о циркуляции
![]() следует, что внутри бесконечно длинного
соленоида
следует, что внутри бесконечно длинного
соленоида
![]() (1)
(1)
где n - плотность витков (число витков на единицу длины).
Найдем магнитную индукцию у конца
полубесконечного соленоида, для чего
представим бесконечный соленоид
состоящим из двух идентичных
полубесконечных, соединяющихся по
плоскости Р (рис.1). В точке М
магнитная индукция В может быть
определена по формуле (1). Если удалить
один из полубесконечных соленоидов,
то, учитывая, что они вносили одинаковый
вклад в магнитную индукцию в точке М,
магнитная индукция у конца полубесконечного
соленоида на его оси будет равна половине
значения
![]() ,
определяемого по формуле (1), т.е.
,
определяемого по формуле (1), т.е.
![]() (2)
(2)
Магнитное поле в точках на оси соленоида конечной длины может быть рассчитано с помощью закона Био-Савара.
Рис.2
Рис.3

![]() соответствует кольцевой ток
соответствует кольцевой ток
![]() ,
где
,
где
![]() - число витков соленоида на единицу его
длины. Как следует из закона Био-Савара,
элемент
- число витков соленоида на единицу его
длины. Как следует из закона Био-Савара,
элемент
![]() кольцевого тока создает в точке О на
оси соленоида поле с индукцией
кольцевого тока создает в точке О на
оси соленоида поле с индукцией
![]()
При определении индукции магнитного
поля кольцевого тока в точке О следует
учесть, что суммарная компонента
магнитной индукции поля, создаваемого
любой парой симметрично расположенных
элементов
![]() ,
направлена вдоль оси
,
направлена вдоль оси
![]() ,
поэтому
,
поэтому

![]()
Так как
![]() ,
то
,
то
![]() ,
и магнитная индукция на оси соленоида
равна:
,
и магнитная индукция на оси соленоида
равна:

Учитывая, что
![]() и
и
![]() ,
где
,
где
![]() - полное число витков соленоида, а
- полное число витков соленоида, а
![]() - его длина, окончательно получим
- его длина, окончательно получим ![]() (3)
(3)
Косинусы углов
![]() и
и
![]() выражаются формулами
выражаются формулами
 ,
,
 (4)
(4)
где
![]() - радиус витков соленоида;
- радиус витков соленоида;
![]() - расстояние от края соленоида до точки,
в которой определяется значение магнитной
индукции.
- расстояние от края соленоида до точки,
в которой определяется значение магнитной
индукции.
Общий вид магнитного поля конечного соленоида изображен на рис.4.
Экспериментальное изучение р
Рис.4
![]() ,
магнитное поле которого исследуется;
маленькой измерительной катушки
,
магнитное поле которого исследуется;
маленькой измерительной катушки
![]() ,
которая введена в соленоид
,
которая введена в соленоид
![]() и может перемещаться вдоль его оси;
баллистического гальванометра
и может перемещаться вдоль его оси;
баллистического гальванометра
![]() ,
соединенного с катушкой
,
соединенного с катушкой
![]() ;
выключателя
;
выключателя
![]() и миллиамперметра
и миллиамперметра
![]() ,
с помощью которого можно измерить ток
в соленоиде
,
с помощью которого можно измерить ток
в соленоиде
![]() (рис.5). При измерении индукции магнитного
поля катушку
(рис.5). При измерении индукции магнитного
поля катушку
![]() устанавливают в какой-либо точке на оси
соленоида
устанавливают в какой-либо точке на оси
соленоида
![]() .
В момент замыкания кнопкой
.
В момент замыкания кнопкой
![]() цепи соленоида
цепи соленоида
![]() ток в нем возрастает от 0 до постоянного
значения
ток в нем возрастает от 0 до постоянного
значения
![]() .
При этом магнитный поток через витки
катушки
.
При этом магнитный поток через витки
катушки
![]() изменяется от 0 до
изменяется от 0 до
![]() ,
где
,
где
![]() - площадь сечения, а
- площадь сечения, а
![]() - число витков катушки
- число витков катушки
![]() .
Изменение магнитного потока приводит
к возникновению в катушке
.
Изменение магнитного потока приводит
к возникновению в катушке
![]() электродвижущей силы индукции по закону
Фарадея:
электродвижущей силы индукции по закону
Фарадея:
Рис.5
![]() ,
,
и, как следствие, появлению в цепи катушки
![]() индукционного тока
индукционного тока
![]() (явление электромагнитной индукции);
в результате чего световой зайчик
гальванометра смещается на угол ,
пропорциональный количеству электричества
(явление электромагнитной индукции);
в результате чего световой зайчик
гальванометра смещается на угол ,
пропорциональный количеству электричества
 ,
протекшего через измерительную часть
установки:
,
протекшего через измерительную часть
установки: ,
где
,
где
![]() - баллистическая постоянная гальванометра.
- баллистическая постоянная гальванометра.
Если полное сопротивление цепи
измерительной катушки
![]() равно
равно
![]() ,
то
,
то
![]() ,
и поэтому
,
и поэтому
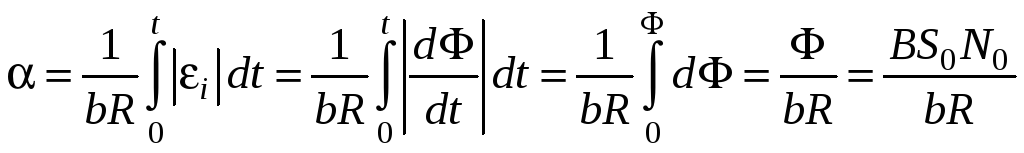
Тогда для магнитной индукции имеем
![]() или
или
![]() (5)
(5)
где постоянная
![]() принимается за цену деления баллистического
гальванометра. По формуле (5) определяются
экспериментальные значения магнитной
индукции поля на оси соленоида.
принимается за цену деления баллистического
гальванометра. По формуле (5) определяются
экспериментальные значения магнитной
индукции поля на оси соленоида.
