Российская Федерация

Департамент образования г.Москвы

ГОУ СПО Технический пожарно-спасательный колледж №57

Реферат

По дисциплине «Техническая иеханика»

Тема: «Построение эпюр изгибающих моментов»

Выполнил: Васильева Д.С. группа 2ПБ-15

Дата защиты «__»____________

Оценка_________________

Москва 2011г.

Содержание

1. Введение

2. Алгоритм посторения эпюр внутренних силовых факторов

3. Виды опорных закреплений

4. Построение эпюр продольных сил

5. Построение эпюр продольных сил и изгибающих моментов в балках

6. Консольные балки

7. Балки на 2х опорах

8. Правила контроля эпюр

9. Пример ,задача

Изгиб в сопротивлении материалов, вид деформации, характеризующийся искривлением (изменением кривизны) оси или срединной поверхности деформируемого объекта (бруса, балки, плиты, оболочки и др.) под действием внешних сил или температуры. Применительно к прямому брусу различают: простой, или плоский, при котором внешние силы лежат в одной из главных плоскостей бруса (т. е. плоскостей, проходящих через его ось и главные оси инерции поперечного сечения; сложный, вызываемый силами, расположенными в разных плоскостях; косой, являющийся частным случаем сложного. В зависимости от действующих в поперечном сечении бруса силовых факторов (рис. 1, а, б) . называется чистым (при наличии только изгибающих моментов) и поперечным (при наличии также и поперечных сил). В инженерной практике рассматривается также особый случай И. — продольный И. (рис. 1, в), характеризующийся выпучиванием стержня под действием продольных сжимающих сил. Одновременное действие сил, направленных по оси стержня и перпендикулярно к ней, вызывает продольно-поперечный И. (рис. 1, г).

Приближённый расчёт прямого бруса на действие И. в упругой стадии производится в предположении, что поперечные сечения бруса, плоские до И., остаются плоскими и после него (гипотеза плоских сечений); полагают также, что продольные волокна бруса при И. не давят друг на друга и не стремятся оторваться одно от другого. При плоском И. в поперечных сечениях бруса возникают нормальные и касательные напряжения. Нормальные напряжения s в произвольном волокне какого-либо поперечного сечения бруса (рис. 2), лежащем на расстоянии y от нейтральной оси, определяются формулой  где M_z — изгибающий момент в сечении, a I_z — момент инерции поперечного сечения относительно нейтральной оси. Наибольшие нормальные напряжения возникают в крайних волокнах сечения 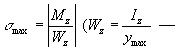 момент сопротивления поперечного сечения). Касательные напряжения t, возникающие при поперечном И., определяются по формуле Д. И. Журавского   где Q_y — поперечная сила в сечении, S_z — статический момент относительно нейтральной оси части площади поперечного сечения, расположенной выше (или ниже) рассматриваемого волокна, b — ширина сечения на уровне рассматриваемого волокна. Характер изменения изгибающих моментов и поперечных сил по длине бруса обычно изображается графиками-эпюрами, по которым определяются их расчётные значения. Под влиянием И. ось бруса искривляется, ее кривизна определяется выражением  где r — радиус кривизны оси изогнутого бруса в рассматриваемом сечении;Е — модуль продольной упругости материала бруса. В случаях малых деформаций кривизна приближённо выражается второй производной от прогиба V, а поэтому между координатами изогнутой оси и изгибающим моментом существует дифференциальная зависимость   называемая дифференциальным уравнением оси изогнутого бруса. Решением этого уравнения определяется упругая линия балки (бруса).

Расчёт бруса на И. с учётом пластических деформаций приближённо производится в предположении, что при возрастании нагрузки (изгибающего момента) первоначально в крайних точках (волокнах), а затем и во всём поперечном сечении возникают пластические деформации. Распределение напряжений в предельном состоянии имеет вид двух прямоугольников с ординатами, равными пределу текучести материала s_т, при этом кривизна бруса неограниченно возрастает. Такое состояние в сечении называется пластическим шарниром, а соответствующий ему момент является предельным и определяется по формуле   в которой S₁ и S₂ — статические моменты сжатой и растянутой частей сечения относительно нейтральной оси.

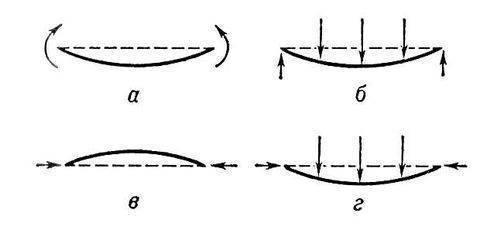Рис.1 Изгиб бруса

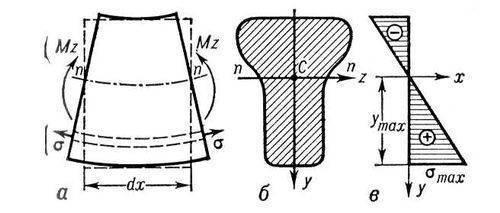
Рис.2 Чистый изгиб бруса

Эпю́ра:

• Эпюра — это схематический чертёж или график. В данном значении практически не употребляется.

Там трёхмерная фигура может проецироваться в несколько ортогональных (по ГОСТу 3, но не всегда) плоскостей. Обычно оно даёт 3 вида: фронтальную, горизонтальную и профильную проекции.

• Эпюра — особый вид графиков.

Она показывает распределение величины при нагрузке на объект. Если это стержень, берётся ось Х и составляются эпюры для сил, напряжений и разных деформаций в зависимости от координаты. Расчет эпюр напряжения является базовой задачей такой дисциплины, как сопротивление материалов. В частности, только при помощи эпюры возможно определить максимально допустимую нагрузку на материал

История

Сведения и приемы построений, обусловливаемые потребностью в плоских изображениях пространственных форм, накапливались постепенно еще с древних времен. В течение продолжительного периода плоские изображения выполнялись преимущественно как изображения наглядные. С развитием техники первостепенное значение приобрел вопрос о применении метода, обеспечивающего точность и удобоизмеримость изображений, т. е. возможность точно установить место каждой точки изображения относительно других точек или плоскостей и путем простых приемов определить размеры отрезков линий и фигур.

Будучи одним из министров в революционном правительстве Франции, Монж много сделал для ее защиты от иностранной интервенции и для победы революционных войск. Начав с задачи точной резки камней по заданным эскизам применительно к архитектуре и фортификации, Монж пришёл к созданию методов, обобщённых им впоследствии в новой науке — начертательной геометрии, творцом которой он по праву считается. Учитывая возможность применения методов начертательной геометрии в военных целях при строительстве укреплений, руководство Мезьерской школы не допускало открытой публикации вплоть до 1799 года (стенографическая запись лекций была сделана в 1795 году).