Министерство образования Республики Беларусь

БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

МЕХАННИКО-ТЕХНОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ

Кафедра: ” Материаловедение в машиностроении“

Курсовой проект

По дисциплине: “ Математическое моделирование “

По теме: “ Решение систем нелинейных уравнений методом конечных разностей“

Выполнил:

Студент группы 104218 Дубатовка С.В.

Проверил: доцент Мельниченко В.В

.

Дата: 08.12.11

Минск 2011

Содержание

Введение…………………………………………………………………………4

МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ………….5

ВЕКТОРНАЯ ЗАПИСЬ НЕЛИНЕЙНЫХ СИСТЕМ…………………………5

МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ, ИЛИ МЕТОД СЕТОК………….........6

ПРИБЛИЖЁННОЕ РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ И ЗАДАЧ О СОБСТВЕННЫХ ЗНАЧЕНИЯХ МЕТОДА КОНЕЧНЫХ РАЗНОСТЕЙ…16

РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ………………………….19

РЕШЕНИЕ ЗАДАЧ В MathCad……………………………………………….23

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ…………………………..33

ВВЕДЕНИЕ

Базовый уровень подготовки инженера-технолога в области информатики и вычислительной техники определяется необходимым набором знаний, умений и навыков в применении ЭВМ для решения различных технических задач.

Специалисты этой категории, помимо умения использовать прикладное программное обеспечение, должны быть программирующими пользователями, т.к. их профессиональная деятельность связана с выполнением большого количества теплотехнических расчетов.

Для соблюдения принципа фундаментальности высшего образования работа построена на базе рассмотрения вопросов применения ЭВМ для решения основных задач теории теплообмена. К одной из таких задач относится задача, связанная с определением температурного поля не одномерных тел численными методами.

Рассмотрим методику подготовки и решения указанной задачи на персональном компьютере.

1. Методы решения систем нелинейных уравнений

Рассматривается ряд методов решения систем алгебраических и трансцендентных уравнений. Среди них метод простых итераций, метод конечных разностей, метод Ньютона в разных модификациях (в частности, n -полюсный метод Ньютона), метод Брауна, метод секущих Бройдена. Показывается связь между данной задачей и за дачей безусловной минимизации функции нескольких переменных. Проводится сравнение методов на примере решения конкретной системы. С единых позиций изучается сходимость основного и упрощенного методов Ньютона и метода, получаемого из метода Ньютона применением итерационного процесса Шульца для приближенного обращения матриц Якоби.

2. Векторная запись нелинейных систем.

Пусть требуется решить систему уравнений

(1.1)

где— заданные, вообще говоря, нелинейные (среди них могут быть и линейные) вещественнозначные функции п вещественных переменных Обозначив

, ,

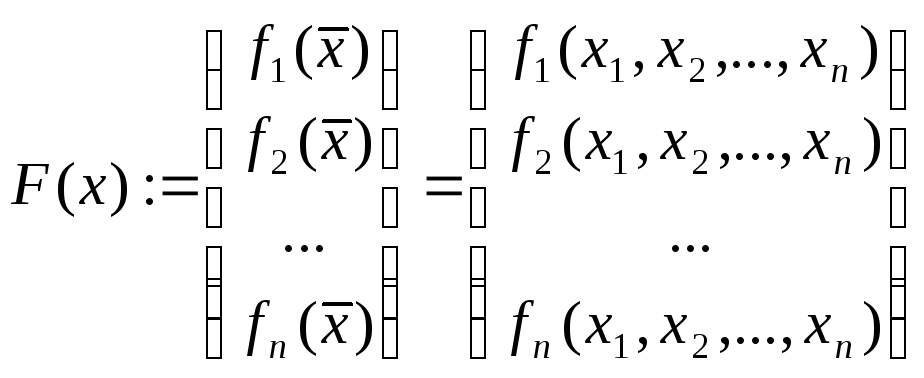данную систему (2.1) можно записать одним уравнением

(1.1а)

относительно векторной функции F векторного аргумента х. Таким образом, исходную задачу можно рассматривать как зада­чу о нулях нелинейного отображения В этой постановке она является прямым обобщением основной задачи предыдущей главы — задачи построения методов нахождения нулей одномерных нелинейных отображений. Фактически это та же задача, только в пространствах большей размерности. Поэтому можно как заново строить методы ее решения на основе разработанных выше подходов, так и осуществлять формальный перенос выведенных для скалярного случая расчетных формул. В любом случае следует позаботиться о правомочности тех или иных операций над векторными переменными и векторными функциями, а также о сходимости получаемых таким способом итерационных процессов. Часто теоремы сходимости для этих процессов являются тривиальными обобщениями соответствующих результатов, полученных для методов решения скалярных уравнений. Однако не все результаты и не все методы можно перенести со случая п = 1 на случай п ≥2. Например, здесь уже не будут работать методы дихотомии, поскольку множество векторов не упорядочено. В то же время, переход от n = 1 до n≥2 вносит в задачу нахождения нулей нелинейного отображения свою специфику, учет которой приводит к новым методам и к различным модификациям уже имеющихся. В частности, большая вариативность методов решения нелинейных систем связана с разнообразием способов, которыми можно решать линейные алгебраические задачи, возникающие при пошаговой линеаризации данной нелинейной вектор-функции F(x).

3. Метод конечных разностей, или метод сеток

Универсальным численным методом решения граничных задач, в основе которых лежат дифференциальные уравнения n-го порядка, являются методы конечных разностей (сеток). Достоинство конечно-разностных методов состоит в том, что они сводят решение краевой задачи для дифференциального уравнения к решению системы алгебраических уравнений относительно значений искомой функции на заданном множестве точек. Это достигается путем замены производных, входящих в дифференциальное уравнение, их конечно-разностными аппроксимациями.

Чтобы решить задачу (1)-(3) методом конечных разностей, необходимо выполнить следующее:

1.     Заменить область непрерывного изменения аргумента дискретным множеством точек, т.е. на отрезке [a,b] строится сетка , где  – узлы сетки , i=0,1,…,n; точки  и - это граничные узлы сетки, все остальные узлы называются внутренними. Величина   i=0,1,…,n-1 называется шагом сетки . Количество и расположение узлов сетки выбирается в зависимости от требуемой точности решения задачи, в частном случае сетка выбирается равномерной, т.е.  и шаг сетки в этом случае выбирается как  h=(b-a)/n.

2.     Заменить (аппроксимировать на сетке) дифференциальное уравнение (1) и граничные условия (2)-(3) разностными уравнениями. Для этого

   в каждом узле сетки _i  определяем сеточную функцию .

   заменяем значения производной отношением конечных разностей;

   переходим от непрерывного дифференциального уравнения относительно функцииu=u(x), (аргумент х – непрерывен) к разностной задаче относительно сеточной функции .

   в итоге  граничная задача (1)-(3) заменяется системой алгебраических уравнений относительно сеточной функции ; Эта система алгебраических уравнений называется разностной схемой.

3.     необходимо решить систему алгебраических уравнений относительно сеточной функции  и тем самым найти таблицу значений этой сеточной функции, являющейся приближенным решением исходной краевой задачи.

Простейшим способом построения конечно-разностной системы алгебраических уравнений является  замена производных через значения функции в узлах сетки. Такая замена может быть получена различными способами.

Рассмотрим линейную краевую задачу

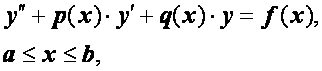(1.24)

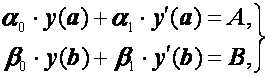(1.25)

,

где , , и непрерывны на [a, b].

Разобьем отрезок [a, b] на n равных частей длины, или шага

.

Точки разбиения 

, 

называются узлами, а их совокупность – сеткой на отрезке [a, b]. Значения в узлах искомой функции  и ее производных   обозначим соответственно через

.

Введем обозначения

Заменим производные так называемыми односторонними конечно-разностными отношениями:

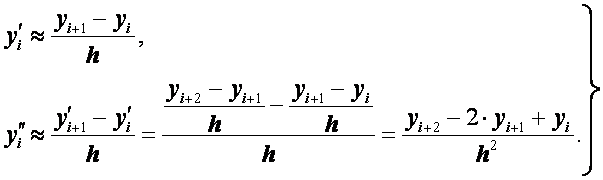(1.26)

Формулы (2.26) приближенно выражают значения производных во внутренних точках интервала [a, b].

Для граничных точек положим

.  (1.27)

Используя формулы (1.26), дифференциальное уравнение (1.24) при , (i=1, 2,..., n–1) приближенно можно заменить линейной системой уравнений

(1.28)

Кроме того, в силу формул (1.27) краевые условия (1.25) дополнительно дают еще два уравнения:

. (1.29)

Таким образом, получена линейная система n+1 уравнений с n+1 неизвестными , представляющими собой значения искомой функции  в узлах сетки. Система уравнений (1.28), (1.29), заменяющая приближенно дифференциальную краевую задачу (1.24), (1.25) обычно называется разностной схемой. Решить эту систему можно каким-либо общим численным методом. Однако схема (1.28), (1.29) имеет специфический вид и ее можно эффективно решить специальным методом, называемым методом прогонки. Специфичность системы заключается в том, что уравнения ее содержат три соседних неизвестных и матрица этой системы является трехдиагональной.

Преобразуем уравнения (1.28):

. (1.30)

Введя обозначения

получим

, (i=0, 1,..., n-2). (1.31)

Краевые условия по-прежнему запишем в виде

. (1.32)

Метод прогонки состоит в следующем.

Разрешим уравнение (1.31) относительно :

. (1.33)

Предположим, что с помощью полной системы (1.31) из уравнения исключен член, содержащий. Тогда уравнение (1.33) может быть записано в виде

, (1.34)

где  и  должны быть определены. Найдем формулы для этих коэффициентов. При i=0 из формулы (1.33) и краевых условий (1.32) следует, что

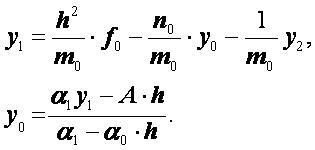
Исключая из этих двух уравнений , найдем

.

Выразим теперь отсюда :

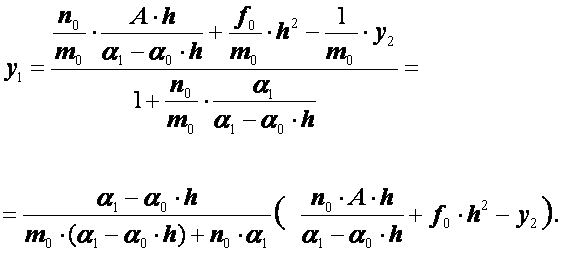(1.35)

Но, согласно формуле (1.34),

(1.36)

Сравнивая теперь (1.35) и (1.36), найдем, что

(1.37)

Пусть теперь i >0, то есть i=1, 2,..., n–2. Выражая  по формуле (1.34), получим:

.

Подставляя это в формулу (2.33), будем иметь

.

Разрешая полученное уравнение относительно, находим

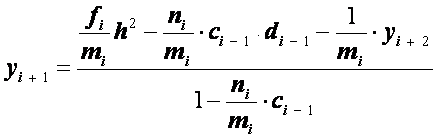, или

. (1.38)

Отсюда, сравнивая формулы (1.34) и (1.38), получаем для коэффициентов и рекуррентные формулы:

 

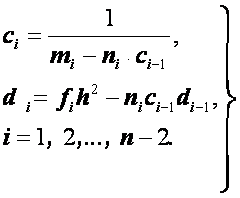(1.39)

Так как  и  уже определены по формулам (1.37), то, используя формулы (2.39), можно последовательно определить коэффициенты  и  до  и  включительно. Эти вычисления называются прямым ходом метода прогонки.

Из формулы (1.33) при i=n–2 и второго краевого условия (1.32) получаем

Разрешая эту систему относительно, будем иметь

. (1.40)

Теперь, используя (1.34) и первое краевое условие (1.32), мы можем последовательно найти . Это − обратный ход метода прогонки.

Итак, получаем следующую цепочку:

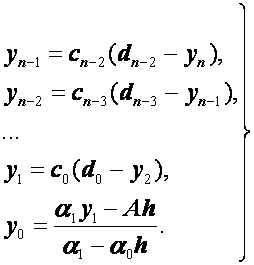(1.41)

Для простейших краевых условий  

формулы для и  упрощаются. Полагая в этом случае из формул (1.37), (1.40), (1.41) будем иметь

Рассмотренный нами подход сводит линейную краевую задачу к системе линейных алгебраических уравнений. При этом возникает три вопроса.

1) Существует ли решение алгебраической системы типа (1.31)?

2) Как фактически находить это решение?

3) Сходится ли разностное решение к точному при стремлении шага сетки к 0?

Можно доказать, что если краевая задача имеет вид

причем р(x)>0, то решение системы (1.31), (1.32) существует и единственно. Фактическое отыскание решения можно провести, например, методом прогонки. На третий вопрос дает ответ следующая

Теорема

Если  и  дважды непрерывно дифференцируемы, то разностное решение, соответствующее схеме с заменой

равномерно сходится к точному с погрешностью  при

Таким образом, схема (1.28), (1.29) дает приближенное решение краевой задачи, но точность ее весьма мала. Это связано с тем, что аппроксимация производной

имеет низкий порядок точности − погрешность этой аппроксимации

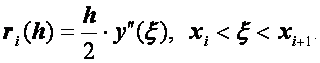
Более точную разностную схему можно получить, если при переходе от линейной краевой задачи к конечно-разностным уравнениям воспользоваться центральными формулами для производных:

, (1.42)

, (1.43)

i=1, 2,..., n.

Погрешность формулы (1.42) выражается так:

то есть формула (1.42) имеет второй порядок точности относительно шага сетки h. Подставляя выражения (1.42), (1.43) в задачу (1.24), (1.25) и выполняя некоторые преобразования, получим следующую систему:

(1.44)

Где .

Система (1.44) снова трехдиагональная и ее решение также можно получить методом прогонки. Его алгоритм здесь будет выглядеть так. Сначала находят коэффициенты

(1.45)

Затем определяют коэффициенты  по следующим рекуррентным формулам:

(1.46)

Обратный ход начинается с нахождения :

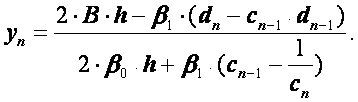(1.47)

После этого находим по формулам:

, (1.48)

. (1.49)

Относительно схемы (1.44) можно также доказать, что она имеет единственное решение пр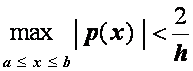и

и ,

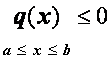и это решение может быть найдено описанным методом прогонки. Кроме того, для схемы (1.44) имеет место

Теорема

Пусть решение граничной задачи (1.24), (1.25) единственно и непрерывно дифференцируемо на [a, b] до четвертого порядка точности включительно. Если выполняются условия

, , 

то схема (1.44) будет равномерно сходиться к решению задачи (1.24), (1.25) с погрешностью .

Заметим, что условия, приводимые в теоремах, являются достаточными, а отнюдь не необходимыми. Поэтому в практике численных расчетов нарушение этих условий обычно не вызывает заметного ухудшения расчетных схем.