47. Жидкость в u-образном сосуде.

В огромном числе случаев при попытке построить модель какого-либо объекта либо невозможно прямо указать фундаментальные законы или вариационные принципы, которым он подчиняется, либо, с точки зрения наших сегодняшних знаний, вообще нет уверенности в существовании подобных законов, допускающих математическую формулировку. Одним из плодотворных подходов к такого рода объектам является использование аналогий с уже изученными явлениями.

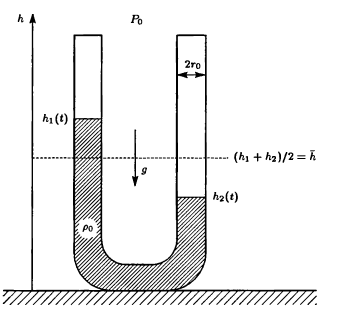
Жидкость занимает часть

сосуда U-образной формы, представляющего собой изогнутую трубку

радиуса rо. Масса жидкости М0, ее плотность рo0. Стенки

сосуда идеально гладкие, поверхностным натяжением пренебрегается,

атмосферное давление Ро и ускорение свободного падения g постоянны.

В состоянии равновесия жидкость, очевидно, покоится, ее высота в обоих коленах сосуда одинакова. Если ее вывести из равновесия, то

начнется движение, характер которого установим с помощью ЗСЭ.

Потенциальную энергию системы вычислим через работу, которую необходимо совершить, чтобы переместить ее из состояния равновесия в положение, изображенное на рисунке.

где Р — вес той части жидкости в левом колене, уровень которой

превышает величину h2. Работа сил атмосферного давления равна нулю,

так как для разных колен соответствующие перемещения направлены

в разные стороны.

Неизвестные величины h1(t) и h2(t) связаны соотношением h1(t) + h2(t) = const > 0, выражающим постоянство полной длины столба жидкости в сосуде с постоянным сечением. Подставляя последнее равенство в выражение для Еп получаем после интегрирования

При вычислении кинетической энергии учтем постоянство сечения

трубки и несжимаемость жидкости. Это означает, что столб жидкости

движется как целое, и ее скорость v(t) одинакова во всех сечениях.

Примем за v(t) величину dh2(t)/dt и тогда

а из ЗСЭ следует

Так как dE/dt = 0, то, продифференцировав это выражение, получаем

что, с учетом такого же соотношения для величины h1(t), дает

уравнение

где h = (h2 — h1)/2 — отклонение уровня жидкости от положения

равновесия.

Т.е. в данной системе будут происходить незатухающие гармонические колебания.

48. Электрический колебательный контур.

В огромном числе случаев при попытке построить модель какого-либо объекта либо невозможно прямо указать фундаментальные законы или вариационные принципы, которым он подчиняется, либо, с точки зрения наших сегодняшних знаний, вообще нет уверенности в существовании подобных законов, допускающих математическую формулировку. Одним из плодотворных подходов к такого рода объектам является использование аналогий с уже изученными явлениями.

Это устройство представляет собой конденсатор, соединенный проводами с катушкой индуктивности. В момент t = 0 цепь замыкается, и заряд с обкладок

конденсатора начинает распространяться по цепи.

Сопротивление проводов будем считать равным нулю, емкость конденсатора равна С, индуктивность катушки L. Для изменяющейся со временем величины q(t), где q(t) — заряд на обкладках

конденсатора, необходимо получить соответствующее уравнение.

Ток i(t) и напряжение u(t) также являются функциями времени.

По физическому смыслу величины С в любой момент времени имеем равенство u(t) = q(t)С (емкость равна величине заряда, который необходимо поместить на обкладки конденсатора для увеличения разности потенциалов между ними на единицу).

Так как электрическое сопротивление в цепи отсутствует, то падения напряжения на проводах нет, и разность потенциалов u(t), существующая на конденсаторе, подается непосредственно на катушку. При переменном токе в катушке возникает электродвижущая сила самоиндукции, равная

= -Ldi/dt. L- Коэффициент пропорциональности между изменением силы тока и ЭДС

Закон Ома для цепи в отсутствие сопротивления выглядит следующим

образом: u(t) = - (t), или q(t)/C = - (t) = Ldi/dt.

Так как по определению i = —dq/dt (i- скорость изменения заряда

Э проходящего через сечение проводника), то из последнего соотношения

получаем уравнение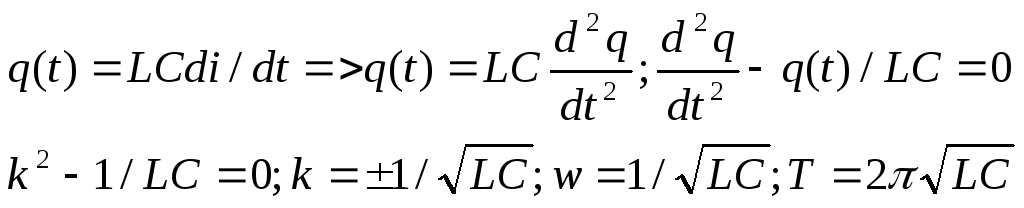

Т.е. в системе «емкость-индуктивность» колебания происходят также, как и в системе «шарик-пружина».