44. Получение модели «шарик-пружина» с помощью принципа Гамильтона.

Воспользуемся принципом Гамильтона для построения модели движения шарика, соединённого с пружиной. В качестве обобщенной координаты выберем координату шарика Тогда обобщенная скорость - обычная скорость шарика. Функция Лагранжа записывается через значения кинетической энергии и потенциальной энергии системы:

L=.

Для величины действия получится выражение .

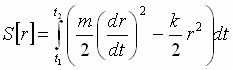Вычислим действие на вариациях координаты

Далее найдем

.

Положим , получим

. Проинтегрируем по частям первое слагаемое

. Тогда, учитывая, что , будем иметь

.

Приравняем 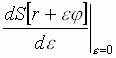нулю. Получим

.

Так как функция - произвольная, то выражение, стоящее под знаком интеграла равно нулю во все моменты

.

Получилось то же уравнение, что и из второго закона Ньютона, и из закона сохранения энергии.

45. Колебание маятника в поле сил тяжести.

Пусть на неподвижном шарнире подвешен маятник – груз массы , находящийся на конце стержня длины . Шарнир считается идеально гладким в том смысле, что в нем не происходит потери энергии на трение. Неподвижность шарнира означает, что от него энергия в системы "стержень - груз" не поступает, такой шарнир не способен совершать над ней какую-либо работу. Стержень считается невесомым и абсолютно жестким. Груз имеет небольшие размеры по сравнению с длиной стержня (материальная точка), ускорение свободного падения  постоянно, сопротивлением воздуха можно пренебречь, колебания происходят в фиксированной вертикальной плоскости.

1.

2. Обобщенная координата - угол отклонения стержня от вертикальной оси. Обобщенная скорость . Кинетическая энергия определяется формулой , а потенциальная энергия выражением , где - отклонение маятника от вертикального положения. Так как потенциальная энергия определяется с точностью до постоянной, то можно опустить величину .

Теперь можно выписать функцию Лагранжа и действие

, .

Находя действие на вариациях ,

и дифференцируя его по , и полагая , имеем (приравнивая результат к нулю)

.

Интегрируя по частям первое слагаемое под знаком интеграла, учитывая, что , будем иметь

,

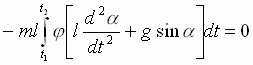которое в силу произвольности может удовлетворяться лишь, если для всех справедливо

Это нелинейное уравнение. Оно линеаризуется при ;

.

Здесь - собственная частота малых колебаний, и мы имеем решение

.

46. Использование принципа Гамильтона для построения моделей механических систем (добавление постоянной внешней силы в систему «шарик-пружина»).

Этот принцип является единственно реальным способом построения моделей для систем, состоящих из большого числа разнообразных элементов, связанных между собой различными способами.

Пусть в системе "шарик-пружина" имеется некоторая дополнительная сила, воздействующая на шарик: .

Применим принцип Гамильтона.

- кинетическая энергия,

- потенциальная энергия,

- функция Лагранжа,

- действие по Гамильтону.

Или

.

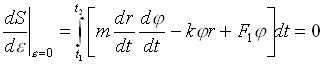- принцип Гамильтона.

Интегрирование по частям первого слагаемого дает

.

Тогда

.

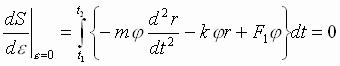Подынтегральное выражение равно нулю

  или