
- •Курсовая работа
- •1.Оглавление
- •2.Цель работы, методы решения, исходные данные.
- •3. Построение точечных графиков диаграмм, гистограмм, отражающих зависимость данных величин.
- •4. Вычисление коэффициентов корреляции и детерминации.
- •5. Нахождение уравнений линейной регрессии y на X первой степени, полинома 2-ой и 3-ей степени. Построение их графиков.
- •6. Оценка статистической надежности результатов регрессионного моделирования.
- •7. Рассчет средней ошибки аппроксимации.
- •9. Выводы.
- •10. Список используемой литературы.
-
7. Рассчет средней ошибки аппроксимации.
Величина отклонений фактических и
расчетных значений результативного
признака y-
![]() по
каждому наблюдению представляет собой
ошибку аппроксимации.
по
каждому наблюдению представляет собой
ошибку аппроксимации.
Поскольку y-
![]() может быть как величиной положительной,
так и отрицательной, то ошибки
аппроксимации для каждого наблюдения
принято определять в процентах по
модулю.
может быть как величиной положительной,
так и отрицательной, то ошибки
аппроксимации для каждого наблюдения
принято определять в процентах по
модулю.
Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению определяют среднюю ошибку аппроксимации:
![]()
1)Для линейной регрессии
![]() =5,19%
=5,19%
2)Для полинома 2й степени
![]() =4,92%
=4,92%
3)Для полинома 3й степени
![]() =3,91%
=3,91%
-
8. Определение прогнозного значения результата(прогнозное значение Х увеличится на 10% от его среднего уровня)и доверительного интервала прогноза для уровня значимости α=0,05
Так как по условию прогнозное
значение X увеличилось на 10%
от его среднего, то считаем это прогнозное
значение умножая среднее X на 1,1. Чтобы
рассчитать прогнозное значение
результата, воспользуемся линиями:
![]() =
a * x = Xпр
+ b (для линейной регрессии первого
порядка),
=
a * x = Xпр
+ b (для линейной регрессии первого
порядка),
![]() =a
* Xпр^2
+ b * Xпр
+ c (для полинома второй степени),
=a
* Xпр^2
+ b * Xпр
+ c (для полинома второй степени),
![]() =
a
* x^3
+ b
* x^2
+ c*x
+ d
(для
полинома третьей
степени).
=
a
* x^3
+ b
* x^2
+ c*x
+ d
(для
полинома третьей
степени).
Xпр = х* 1,1
1) для линейной регрессии:
![]() =66.57177863
=66.57177863
2)для полинома 2й степени:
![]() =64.85016398
=64.85016398
3)для полинома 3й
степени:
![]() =65.67360883
=65.67360883
Доверительный интервал рассчитываем по формуле:
![]() - tγ
*
- tγ
*
![]() ≤ Y*
≤
≤ Y*
≤
![]() + tγ
*
+ tγ
*
![]()
Величину
![]() считаем по формуле:
считаем по формуле:
![]() =s*
=s*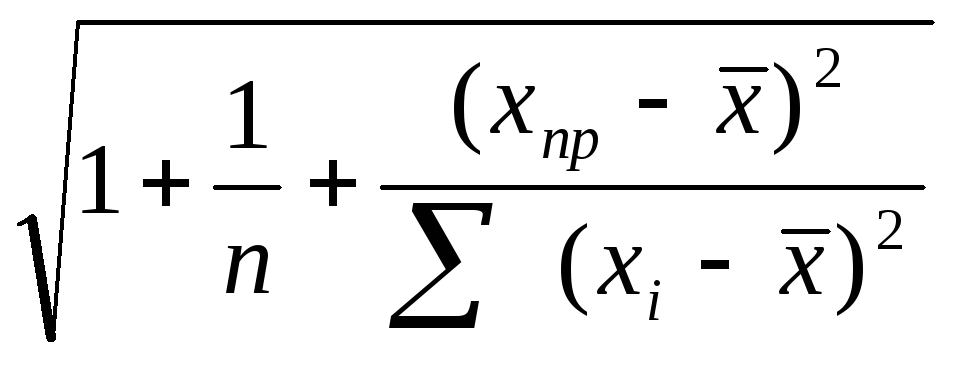
![]() ,
где s=
,
где s=![]() ,
а
,
а
s2= Dост
, т.к α=0,05
![]() γ=0,95
γ=0,95
![]() tγ=2,13;
tγ=2,13;
Для регрессии s =
4.682985194,
![]() = 4.885177258
= 4.885177258
Для полинома 2й степени s
= 4.428417934,
![]() = 4.59124963
= 4.59124963
Для полинома 3й степени s
= 3.906811202,
![]() = 4.050463564
= 4.050463564
Доверительный интервал:
1)Для регрессии 56.23025107 ≤ Y* ≤ 76.91330619
2)Для полинома 2й степени 55.07080227 ≤ Y* ≤ 74.6295257
3) Для полинома 3й степени 57.04612144 ≤ Y* ≤ 74.30109622
-
9. Выводы.
На основе произведённых вычислений можно сделать вывод, что исследуемые величины коррелированны, они зависимы друг от друга (т.к. коэффициент корреляции не равен нулю), то есть связь между долей расходов населения на питание в зависимости от пенсии потребителя достаточно обоснована, но неоднозначна.
Так как Fфакт > Fтабл во всех трех случаях, нулевая гипотеза об отсутствии связи признаков отклоняется, т.е. Fфакт > Fтабл, H0 отклоняется.
-
10. Список используемой литературы.
-
Гмурман В.Е. Теория вероятностей и математическая статистика. - М: Высшая школа, 2000.
-
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М: Высшая школа, 2000.
-
Мазный Г.Л., Прогулова Т.Б. Методическое пособие к курсовому проектированию по высшей математике и информатике. – Д: Дубна, 1996.
-
Елисеева И.И. Практикум по эконометрике: Учеб. пособие. – М.: Финансы и статистика, 2003.
-
Елисеева И.И. Эконометрика: учебник. – М.: Финансы и статистика, 2003.
