4. Неперервні випадкові величини (нвв)

Def. 4.1 Інтегральною функцією розподілу ВВ функція, яка у кожній точці дорівнює імовірності того, що ВВ приймає значення, менше за :

(4.1)

Приклад ДВВ.

	0	1	2	3

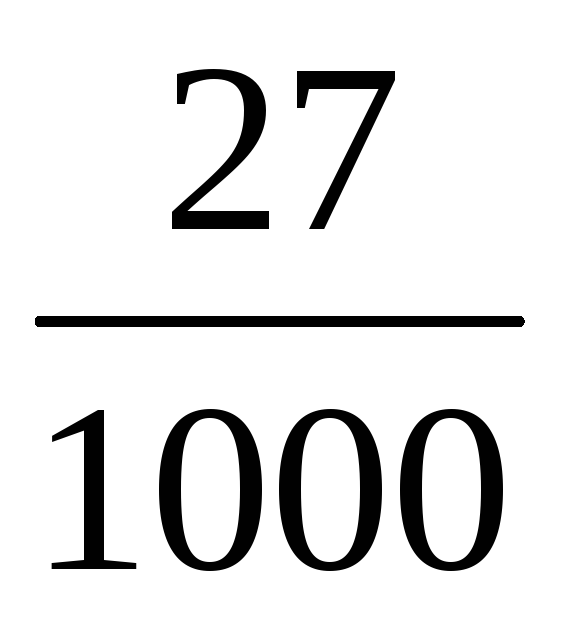
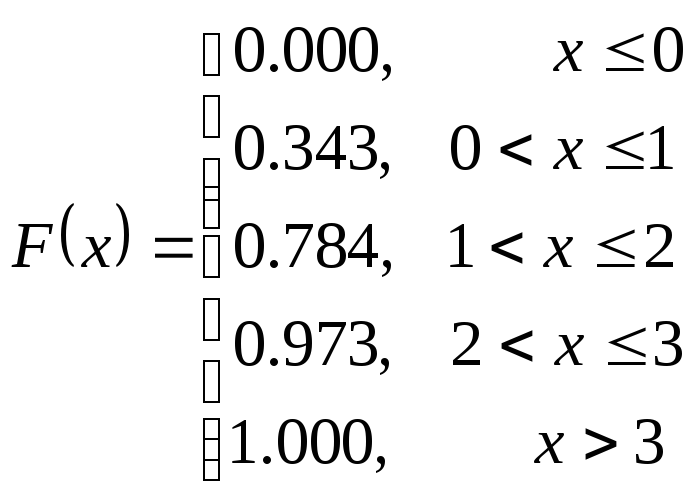
Властивості.

1) ; 2) ; 3) Неспадна: ;

4) . Частинний випадок: Якщо спектр ВВ належить проміжку , то при .

Доведення 3). Нехай , тоді:

Наслідок:

(4.2)

Інтегральна функція ДВВ, яку ми побудували є розривною. Існують ВВ з неперервною інтегральною функцією розподілу.

Приклад.

Def. 4.2 ВВ називається неперервною якщо її інтегральна функція неперервна та має похідну, крім, можливо, скінченної множини точок.

Однією з особливостей НВВ є те, що імовірність будь якого точного її значення дорівнює нулю. Дійсно,

(4.3)

У таких ВВ існую т. з. диференціальна функція розподілу (функція щільності імовірності)

Def. 4.3 Диференціальною функцією розподілу (функцією щільності імовірності) НВВ називається похідна від її інтегральної функції розподілу:

(4.4)

Зрозуміло, що вона визначена там, де існує похідна від .

З означення випливає, що ДФР існує лише у НВВ на відмінну від ІФР, яка є як у НВВ, так і у ДВВ.

Властивості:

1) , крім, можливо скінченної множини точок;

2) , оскільки це похідна неспадної функції (ІФР);

3) імовірність влучення у інтервал:

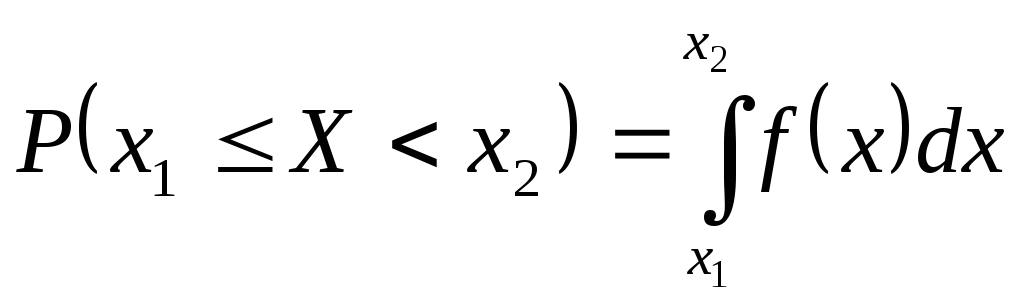(4.5)

Доведення. За (4.2)

Формула Ньютона - Лейбніца, означення 4.3 (формула (4.4)).

4) (4.6)

Доведення: За (4.5)

Якщо спектр ВВ належить проміжку , то .

5) . Доведення від протилежного. За 4) площа під криволінійної трапеції дорівнює одиниці. Якщо, приміром, , то невласний інтеграл буде розбіжним.

Якщо спектр ВВ належить проміжку , то при . Дійсно, за властивостями ІФР, при , тобто на обох інтервалах є сталою, похідна якої дорівнює нулю.

6) Зв'язок з ІФР:

(4.7)

Дійсно, за (4.5).Зауваження: змінна за якою ведеться інтегрування.

Числові характеристики НВВ.

Def. 4.4 Математичним сподівання НВВ називається невласний інтеграл:

(4.8)

за умовою, що він збігається.

Дисперсія та середнє квадратичне відхилення визначаються так само, як і для ДВВ.

Формула для обчислення дисперсії набуває вигляду:

(4.9)

Приклади.

1. Дана функція

Довести що вона є ІФР НВВ, побудувати ДФР, обчислити математичне сподівання і дисперсію та ймовірності:

, .

.

, .

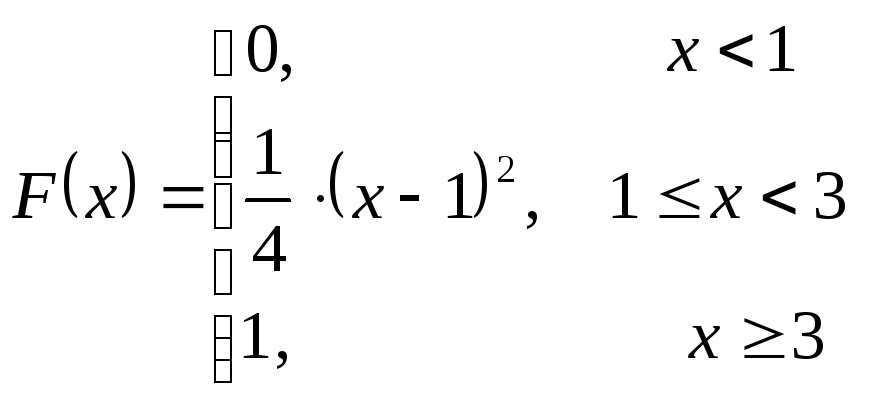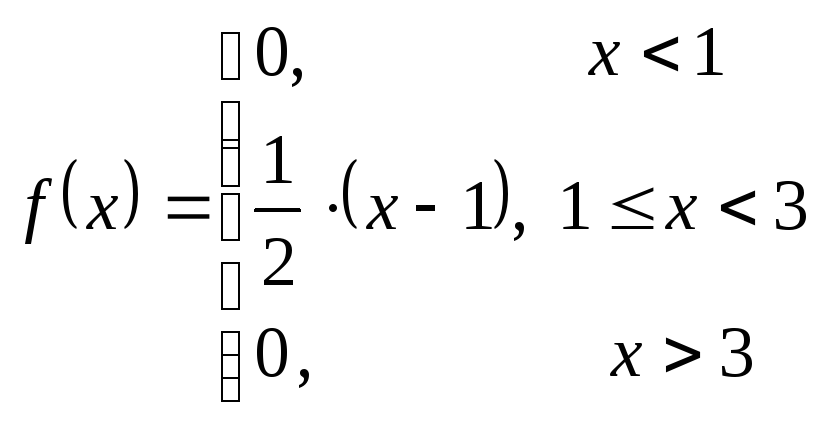Зауваження. .

2. Дана функція .

Знайти значення параметра при якому вона є ДФР НВВ та побудувати ІФР.

.
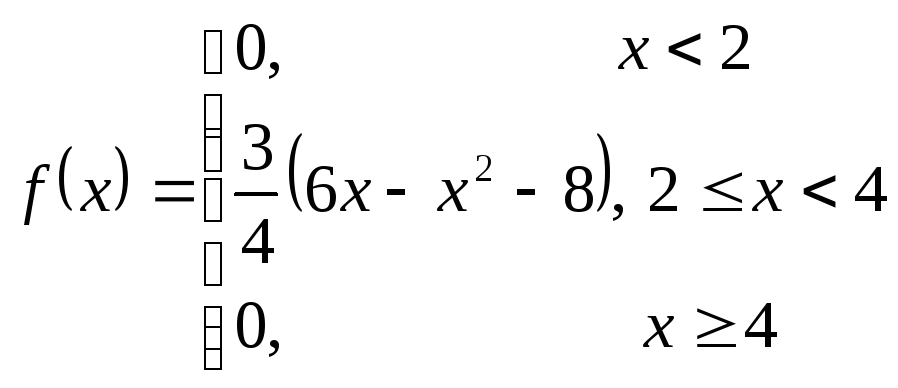