3. Незалежні повторні випробування

Схема повернених куль.

Нехай у кожному з випробувань подія настання події відбувається із сталою імовірністю , тобто імовірність її настання не залежить від того, що відбувалось у попередніх випробуваннях, і настання чи не настання її не впливає на подальше. Такий процес називається НПВ. Позначимо імовірність події , тобто імовірність не появи через .

Def. 3.1 Кількість випробувань, в яких сталася подія називається

частотою події. При НРВ її позначають . (Зауваження)

За Def. 1.15 відносна частота або частість:

Знайдемо числові характеристики ДВВ .

Розглянемо набір ДВВ , кожна з яких приймає два значення: 1, якщо у -тому випробуванні подія сталася і 0, якщо не сталася.

Закон розподілу:

	1	0

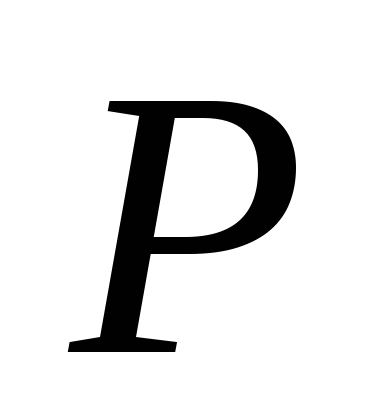
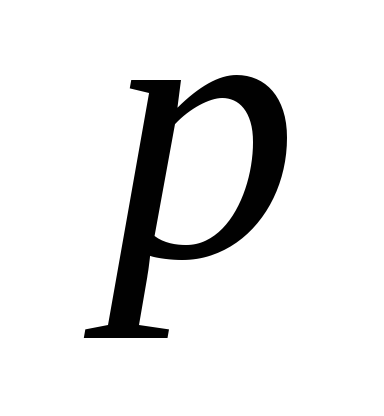
Зрозуміло, що

Оскільки всі ці ДВВ мають однакові закони розподілу, то їх числові характеристики однакові.

Обчислимо , . Отже .

Тоді: (3.1)

(3.2)

(3.3)

Якщо ДВВ, то частість також, причому стала. Знайдемо

(3.4)

(3.5)

(3.6)

Теорема 3.1 Формула Бернуллі.

Нехай при проведенні випробувань в кожному з них подія може статися з імовірністю . Тоді імовірність того, що подія станеться рівно разів дорівнює:

(3.7)

де - число сполук, імовірність події , тобто не настання події .

Доведення:

Розглянемо приклад =3. Випишемо ПГЕП:

…

У загальному випадку. Простір елементарних подій складається добутків подій . Вони утворюють ПГЕП. Їх кількість ? Нас цікавлять випадки, коли сталася разів, тобто такі добутки, які містять множників , відповідно множників буде . Імовірність кожної такої елементарної події буде дорівнювати добутку імовірностей,? отже дорівнює . Ці події попарно несумісні, отже імовірність суми дорівнює сумі імовірностей. Таких елементарних подій буде ?.Отримаємо формулу.

Приклад. =3,

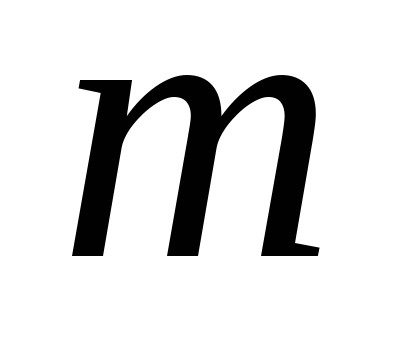
	0	1	2	3

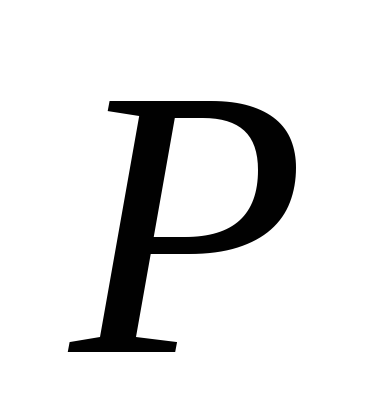
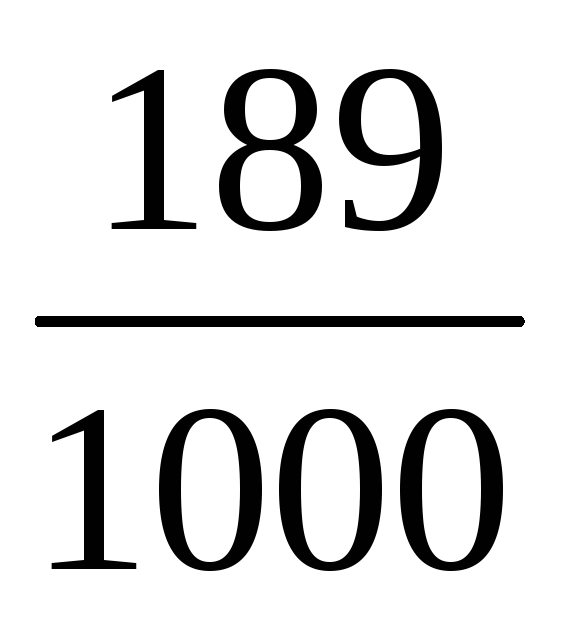
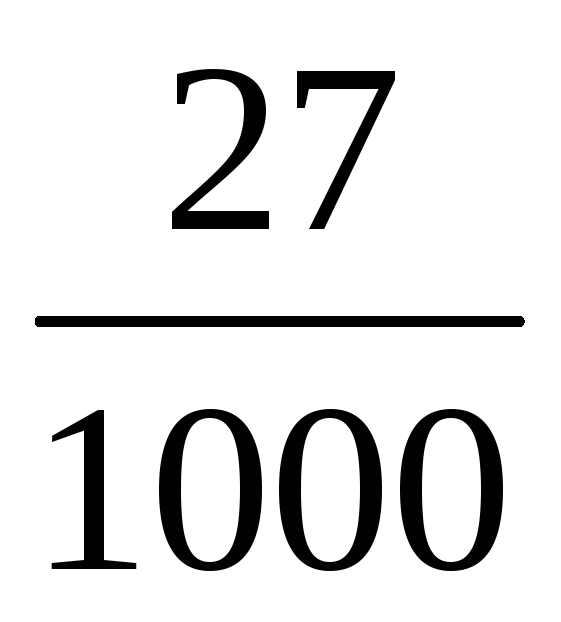
Графік.

Закон розподілу частоти:

	0	1	...		...
			...		...

Цей закон називається біноміальним.

Числові характеристики цього закону розподілу знайдені раніше.

Назва походить з того, що праві частини формули Бернуллі можна розглядати як загальний член розкладу бінома Ньютона:

.

Звідси, враховуючи, що , отримаємо:

(3.8)

головна вимога до закону розподілу ДВВ.

Def. 3.2 Модою закону розподілу називається частота, якій відповідає найбільша імовірність. Позначається .

Уномодальний (бімодальний) розподіли. Полігон розподілу має один (два) максимум.

Неважко довести, що біноміальний розподіл є уномодальним. Дійсно, оцінимо співвідношення сусідніх ймовірностей:

Остаточно, маємо: . Таки чином, при наступна ймовірність більша, ймовірність зростає, а при - спадає і моду можна знайти із умови виконання таких нерівностей

(3.8)

Дослідимо першу з них:

Остаточно маємо:

(3.9)

Нерівності нестрогі, отже якщо ціле число, а , то і - ціле на одиницю більше. Таким чином два сусідніх числа визначають моду.

Два типи задач. 1) Імовірність події , кількість випробувань . Знайти моду. , .

2) Мода , яка кількість випробувань?

Теорема 3.2 Локальна теорема Лапласа

Якщо імовірність настання події у кожному з незалежних випробувань є сталою і дорівнює , а кількість випробувань, достатньо велика, то імовірність настання події рівно разів приблизно дорівнює:

(3.10)

де , - функція Гауса. ЇЇ графік – крива Гауса.

(Без доведення)

Властивості та графік.

1. . 2. Невід’ємна. 3. Парна. 4. Має похідні першого та другого порядку. 5. Має один екстремум, максимум, у точці , . 6. Дві точки перегину при . 7. та дуже швидко. 8. Табульована.

Продовження прикладу: Знайти імовірність моди.

очне значення: , за формулою Лапласа:

, , . Остаточно, , похибка: 1,1%.

Теорема 3.3 Теорема Пуассона

Якщо імовірність настання події , , у кожному випробувані прямує до нуля при необмеженому зростанні кількості випробувань, , і при цьому добуток прямує до сталого числа , то границя імовірності того, що подія станеться разів дорівнює:

(3.11)

(Без доведення)

Формула Пуассона. Якщо імовірність події маленька , кількість випробувань достатньо велика та величина не перевищує 10, то імовірність настання події разів приблизно дорівнює:

(3.12)

Приклад.

У партії 5000 виробів. Під час транспортування, з імовірністю 0,0002 можливе пошкодження. Знайти імовірність того, що 3 вироби виявляться пошкодженими.

За (3.12): достатньо велике, - маленьке, добуток не перевищує 10. Тому .

При досліджені процесів, в яких виконуються умови теореми Пуассона та кількість випробувань є необмеженою, частоту можна вважати ДВВ з нескінченним ліченим спектром. Закон розподілу цієї ДВВ має вигляд:

			…		...
			…		...

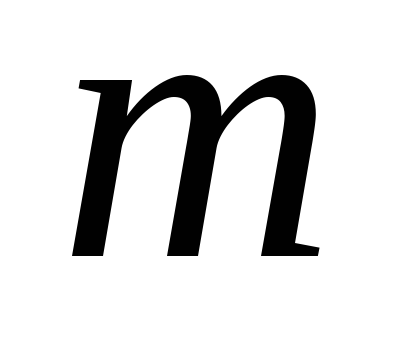
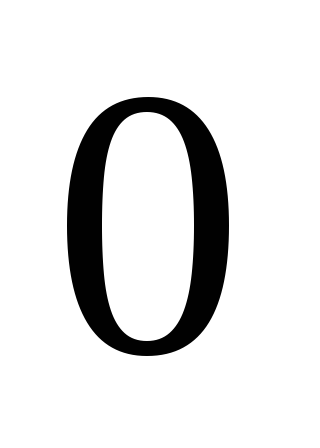
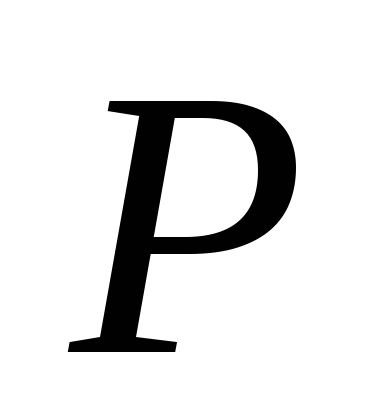
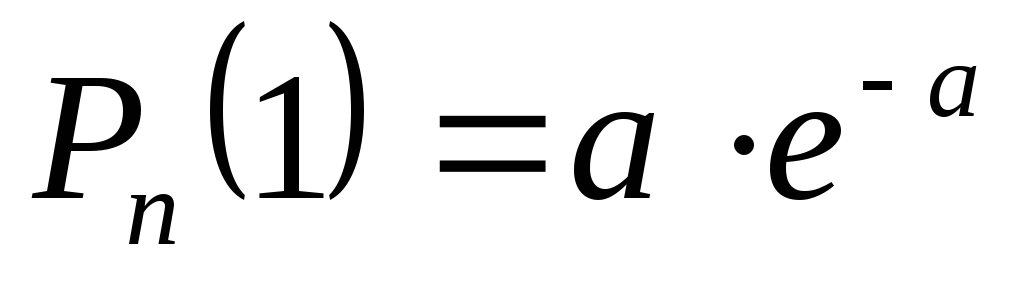
Він законом Пуассона або законом рідких подій.