6 Игры с природой
Издатель обратился в отдел маркетинга, чтобы выяснить предполагаемый спрос на книгу.
Исследования показали: предполагаемый спрос в ближайшие четыре года (штук): 2000, 3000, 4000 или 5000.
Вероятности спроса (соответственно): 0,1+ 0,005*16; 0,5; 0,2; 0,2 – 0,005*16.
Доход от реализации книги составит (100 + 16 ) руб. за книгу. Если книга не продастся, убытки составят (50- 0,5*16) руб. за книгу. Если издатель не удовлетворит спрос, убытки (упущенная выгода) составят (10 + 0,5*16) руб. за книгу.
Используя, по очереди, различные критерии принятия решений в условиях неопределенности и риска определить, сколько книг должно быть издано в расчете на четырехлетний период.
Вероятности спроса (соответственно): 0,18; 0,5; 0,2; 0,12.
Доход от реализации книги составит 116 руб. за книгу. Если книга не продастся, убытки составят 42 руб. за книгу. Если издатель не удовлетворит спрос, убытки (упущенная выгода) составят 18 руб. за книгу.
Используя, по очереди, различные критерии принятия решений в условиях неопределенности и риска определить, сколько книг должно быть издано в расчете на четырехлетний период.
|
решение |
2 |
3 |
4 |
5 |
|
2 тыс. книг |
116*2 |
116*2-18 |
116*2-18*2 |
116*2-18*3 |
|
3 |
116*2-42 |
116*3 |
116*3-18 |
116*3-18*2 |
|
4 |
116*2-42*2 |
116*3-42 |
116*4 |
116*5-18 |
|
5 |
116*2-42*3 |
116*3-42*2 |
116*4-42 |
116*5 |
неопределенность
|
решение |
2 |
3 |
4 |
5 |
|
2 тыс. книг |
232 |
214 |
196 |
178 |
|
3 |
190 |
348 |
330 |
312 |
|
4 |
148 |
306 |
464 |
562 |
|
5 |
106 |
264 |
422 |
580 |
неопределенность
1. Критерий крайнего оптимизма.
=
580- выпускать книги в количестве 5 тыс.
2. Критерий Вальда.
=
190- выпускать книги в количестве 3 тыс.
3. Критерий Гурвица.
Пусть коэффициент пессимизма λ равен 0,6.
Тогда
=
max(0,6*178+0,4*232;
0,6*190+0,4*348; 0,6*148+0,4*562; 0,6*106+0,4*580) = max(199,6;
253,2; 313,6; 295,6) = 313,6. Т.е. выпускать книги в
количестве 4 тыс.
4. Критерий Сэвиджа.
Матрица потерь (рисков).
|
решение |
2 т. (0,18) |
3 (0,5) |
4 (0,2) |
5 (0,12) |
|
2 т. |
0 |
134 |
268 |
402 |
|
3 |
42 |
0 |
134 |
268 |
|
4 |
84 |
42 |
0 |
18 |
|
5 |
126 |
84 |
42 |
0 |
неопределенность
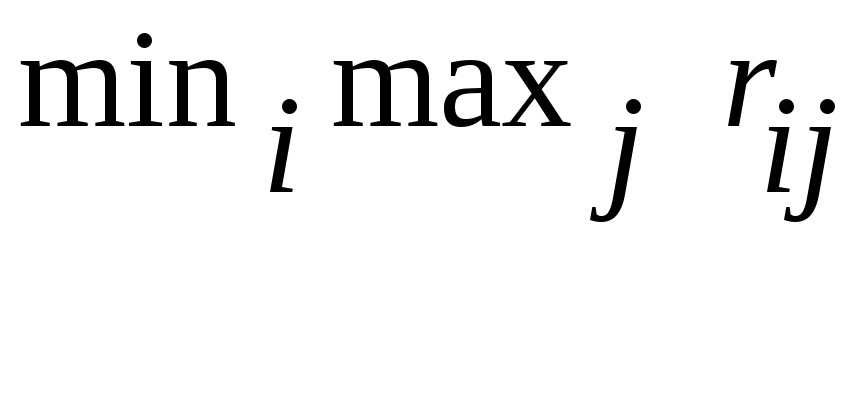=84
- издать 4 т. книжек
5. Критерия Лапласа.
Критерий Лапласа является наиболее разумным, логически обоснованным критерием, т.к. учитывает математическое ожидание.
max(232*0,18 + 214*0,5 + 196*0,2 + 178*0,12; 190*0,18 + 348*0,5 + 330*0,2 + 312*0,12; 148*0,18 + 306*0,5 + 464*0,2 + 562*0,12; 106*0,18 + 264*0,5 + 422*0,2 + 580*0,12) = max(41,76+107+39,2+21,36; 34,2+174+66+37,44; 26,64+153+92,8+67,44; 19,08+132+84,4+69,6) = max(209,32; 311,64; 339,88; 305,08) = 339,88, т.е. издать 4 т. книг.
Выводы
Таким образом, в процессе написания курсовой работы были решены следующие задачи: