
метода РАЗРАБОТКА ТЕРРИТОРИАЛЬНОЙ МОДЕЛИ 2013
.pdf
Расстояние между параллельными прямыми линиями сетки однородной территориальной модели сети подвижной связи можно определить по формуле
h R R sin , км |
(8) |
Смещение BS, расположенных на соседних параллельных линиях сетки относительно друг друга, можно определить по формуле для сотовых сетей
|
|
|
|
|
|
|
|
d |
Zп |
|
R 3 |
|
, км |
(9) |
|
2 |
2 |
|
|
||||
|
|
|
|
|
|
||
В качестве единицы масштаба в территориальной модели можно
принять нормированное расстояние между узлами (BS) равное R 
 3 для сотовой модели. В результате все расстояния в модели будут определяться целыми числами и можно ввести относительные координаты размещения базовых станций (x,y) = (a,b).
3 для сотовой модели. В результате все расстояния в модели будут определяться целыми числами и можно ввести относительные координаты размещения базовых станций (x,y) = (a,b).
Можно построить территориальную модель однородной сети сухопутной подвижной связи. Начальные оси разместить под углом φ. Начальную (первую) соту можно разместить в центре кластера, если это возможно или любую другую соту, с учетом того, что построение будет периодически повторятся вокруг сот первого кластера, по правилу (а,b). Это можно увидеть на графическом представлении территориальной модели рисунка 7. Так как в задании на КП указано, что плотность населения в соте 1 в = 6 раз превышает плотность населения в остальных сотах, то соту 1 можно построить шестисекторной (рисунок 7) или увеличить число каналов.
21
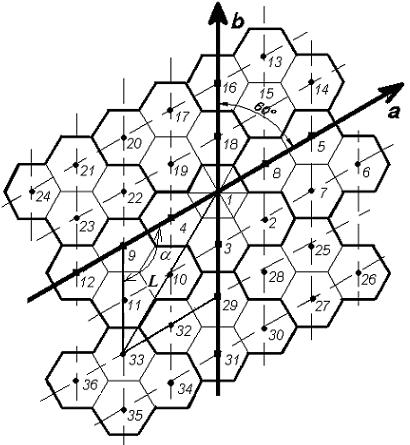
Рисунок 7 – Графическое представление территориальной модели сотовой сети с параметрами a=0,b=2
Параллельно осям размещаем сетку территориальной модели, показывая её более тонкими пунктирными линиями. Заданное количество кластеров К размещаем так, чтобы они охватывали всю обслуживаемую территорию и располагались как можно плотнее друг к другу. Форма обслуживаемой территории должна приближаться к форме круга, если это возможно.
Затем можно рассчитать защитный интервал для сотовой сети по формуле
22

|
|
|
|
D R 3(a2 a b b2 ) , км |
(10) |
||
Для квадратной ячейки есть два значения D1 |
и D2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
D R |
a2 a b b2 , км |
(11) |
|||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
D |
R |
2(a2 a b b2 ) , км |
(12) |
||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
А также можно рассчитать уровень уменьшения соканальных (ин- |
|||||||||||
терференционных) помех по формуле для сотовой сети |
|
||||||||||
|
|
|
|
|
|
|
|
||||
q |
3 (a2 a b b2 ) |
(13) |
|||||||||
И для квадратной территориальной структуры сети |
|
||||||||||
|
|
|
|
|
|
|
|||||
q |
|
a2 a b b2 |
(14) |
||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
q |
2 |
|
|
|
2 (a2 a b b2 ) |
(15) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Зная площадь соты (ячейки), Sс, можно рассчитать площадь кластера по формуле
Sкл = SсС, км2 |
(16) |
И площадь всей сети |
|
S= SсК, км2 |
(17) |
В построенной сети расстояние от центра любого шестиугольника до начала координат составляет
|
|
|
|
|
|
|
|
|
|
|
L |
3 R |
|
a2 a b b2 , км |
(18) |
||||||
А при аппроксимации территории квадратами |
|
|||||||||
|
|
|
|
|
|
|
|
|
||
L R a2 |
a b b2 , км |
(19) |
||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 a b b2 , км |
|
|||
L |
2 R |
|
(20) |
|||||||
2 |
|
|
|
|
|
|
|
|
|
|
23

Выражения для L прямо следуют из обобщенной теоремы Пифагора, которая утверждает, что квадрат длины стороны L, лежащей
напротив угла , образованного сторонами с длинами a и b, равен
L2 a2 b2 2 a b cos |
(21) |
||||
где, в случае изображенном на рисунке 7 |
|
||||
|
|
|
|
||
a 2 3 R и b 2 3 R , а угол 120 . |
|
||||
Таким образом, a 2 и b 2 . Тогда длина L – |
это расстояние |
||||
между BS 1 и BS 33 на рисунке 7. |
|
||||
Фигура образованная BS c номерами 1, 9, 33 и 29 образует ромб совмещенных каналов. В середине этого ромба нет BS c одинаковым набором каналов. Ромб совмещенных каналов можно разделить на два треугольника совмещенных каналов. В общем, всю территорию можно разделить на такие ромбы совмещенных каналов и характеризовать электромагнитную совместимость базовых и мобильных станций. Поэтому необходимо провести расчеты расстояния L для полученного значения параметров ромба совмещенных каналов территориальной модели построенной в КП. Для квадратной структуры необходимо указать квадрат совмещенных каналов, используя сведения расположенные выше.
Необходимо продолжить построение территориальной модели однородной сотовой или другой, например, сети построенной квадратами. Сотовая структура представлена на рисунке 7, на ней обозначены кластеры линиями большей толщины.
Общее количество сот G и кластеров K должно соответствовать заданию на КП и должно быть показано на графическом представлении территориальной модели. Необходимо выполнить требование, чтобы соты (квадраты) с одинаковым набором частот располагались на расстоянии (a,b).
Необходимо обозначить на территориальной модели места расположения BS. BS размещаем в центре сот или по другому (для территориальных планов 3 из 9 и 4 из 12 в центре трех сот), согласно требованиям задания (таблица 1). Присвоим им номера p, где p − целые числа
24

и присваивать их необходимо так, чтобы номера p соответствовали порядку следования кластеров и расстоянию (a,b), то есть через размерность кластера C.
Необходимо разработать правило или систему нумерации сот (квадратов) и BS такое, чтобы, соблюдая его, можно было проводить дальнейшее развитие сети на соседние территории. Номера сот (квадратов) с одинаковыми каналами должны отличаться на величину mC, где m – целые числа. Например, для рисунка 3 нумерацию можно приводить согласно уравнению (a p, b p), так чтобы между сотами, в которых излучаются одни и те же радиоканалы, было расстояние mC.
Необходимо определить относительные координаты размещения BS с помощью сетки нанесенной на территориальном плане. Расстояние между ближайшими базовыми станциями и узлами сетки Zn, км. Координаты можно определить, как в декартовой системе координат, начиная с центра первой соты (квадрата), выбранной ранее. Тогда, например, для BS этой соты 1 имеем координаты (0,0).
Применяя созданное правило или систему нумерации, можно пронумеровать все BS и указать координаты для них. Если территориальный план построен правильно, то линии сетки пересекаются в центрах сот (кроме 3 из 9 и 4 из 12), указывая место размещения BS с коорди-
натами (а, b), где a − ордината, расстояние кратное Zn 
 3 R , км по
3 R , км по
оси Х, а b − абсцисса, расстояние по оси Ỵ. Каждая BS имеет свои координаты. Например, можно записать их для семи BS в виде таблицы 3, используя территориальную модель рисунка 7. Необходимо указать относительные координаты всех базовых станций для сот заданных в КП. Рассмотренное построение можно отнести к территориальному плану 3 из 9 и 4 из 12, учитывая, что одна BS формирует три соты и находится в центре этих трех сот.
Таблица 3 − Координаты размещения семи BS
NBS |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Коорди- |
(0,0) |
(1,-1) |
(0,-1) |
(-1,0) |
(2,0) |
(3,-1) |
(2,-1) |
наты BS |
|
|
|
|
|
|
|
(а, b) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25

В территориальной модели с прямым расширением спектра DSSS все BS кластера могут работать в одном выделенном диапазоне частот одновременно, при этом распределяются кодовые каналы. В таких сетях BS могут различаться не частотными каналами, а разными циклическими сдвигами скремблирующей последовательности и расширяющего кода. Для различных базовых станций сдвиг может осуществляться с шагом по времени кратным периоду ПСП. Необходимо выбрать минимальный шаг сдвига расширяющего кода. Длительность шага сдвига можно определить по формуле
c 1 , с ( 22)
Сч
где Сч – скорость формирования разрядов ПСП. Она приведена в таблице 4.
– количество разрядов. Оно может выбираться равным количеству разрядов расширяющего кода.
Количество BS, имеющих универсальный расширяющий неповторяющийся код в сети, можно рассчитать по формуле
|
|
k |
|
|
nBS |
|
2 |
, |
(23) |
r |
||||
|
|
2 |
|
|
где k – старшая степень скремблирующего полинома; r – старшая степень расширяющего полинома.
Для сетей стандарта CDMA, CDMA 2000, IMT-MC-450 и IMT-EV- DO значения k и r приводятся в [2, с.296–303]. Для сетей WCDMA (UMTS) k изменятся от 18 до 25, а r – от 1 до 9. Для сети IEEE802. 11b используется код Баркера. [2, с. 300].
Значения порождающих, скремблирующих, расширяющих полиномов и скорости их следования Сч для различных базовых технологий сетей приведены в таблице 4.
26

Таблица 4–Порождающие и скремблирующие полиномы
Стандарт СПС |
Порождающий |
Скремблирующий полином |
|
||||||||
|
полином и Сч, |
|
|
|
|
|
|
|
|
|
|
|
Мчип/с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
WCDMA(UMTS) |
Код OVSF длиной |
g(x) x18 x7 1 |
|
|
|
|
|||||
|
до 512 чипов, ско- |
|
|
|
|
|
|
|
|
|
|
|
рость 3,84 |
|
g(x) x18 x10 x7 x5 1 |
|
|||||||
|
|
|
Для режима TDD |
|
|
|
|
||||
|
|
|
g(x) x8 x7 x5 x 1 |
|
|||||||
|
|
|
g(x) x8 x7 x5 x4 1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
CDMA2000, IMT- |
Код Уолша |
дли- |
gi (x) x |
15 |
|
13 |
x |
9 |
x |
8 |
|
450 и IMT-EV-DO |
ной 64–256 |
чипов |
|
x |
|
|
|
||||
x7 x5 |
x1 |
|
|
|
|
|
|||||
|
(Wmn), скорость |
|
|
|
|
|
|||||
|
3,68 |
|
|
|
|
|
|
|
|
|
|
IEEE 802.11 |
Код Баркера дли- |
g(x) x36 x26 x23 x22 |
|
||||||||
|
ной от 7 до 11 чи- |
x16 x12 x11 x10 x8 |
|
||||||||
|
пов |
|
|
||||||||
|
(10110111000), |
x7 x5 x4 |
x2 |
x 1 |
|
|
|||||
|
скорость 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для назначения номеров BS необходимо порождающий полином g(x) или выбранную ветвь кодового дерева кода OVSF умножить (сдвинуть) на xi (на i разрядов), затем еще на i разрядов и так далее для всех BS количество которых можно выбрать равным размерности кластера C.
g(x) g(x) xi , |
(24) |
где i – степень сдвига кодовой комбинации, надо выбрать равной длине расширяющей последовательности или двум, трем и т.д. длинам.
Значения кодов можно записать числом. Необходимо разработать систему нумерации BS и представления больших чисел. Полученный
27
сдвиг относительно начала координат скремблирующей последовательности и может отличать BS. Он отличается на выбранную длину расширяющего кода.
Например, для сети стандарта WCDMA (UMTS) в качестве расширяющего применяется код OVSF. С помощью кодового дерева кода по [2, с.475] выбираем одну ветвь, например, 1,1,0,0. Сдвигать необходимо на то количество разрядов, которое имеет расширяющий код или на кратное. В данном примере это 4 разряда, тогда:
11002(1210) – номер BS – 1, следующий сдвиг 110000002(19210) – номер BS – 2, 1100000000002(307210) – номер BS – 3, и так далее до 218 разрядов согласно параметрам кодового дерева и значению скремблирующей последовательности таблицы 4. Можно ограничиться заданным количеством BS, которое равно количеству BS в кластере. Но необходимо исключить шум не ортогональности, исключив сдвиги, взаимная корреляция которых не равна нулю. Например, 11000000 и 110000000000 не коррелируют, так как поразрядное перемножение и суммирование их произведений равно нулю. Если такие кодовые сдвиги имеются их нельзя применять, нужно выбрать другие и использовать не ортогональные для различения BS.
По построенной модели однородной сотовой сети с прямым расширением спектра, например, рисунка 7 необходимо определить относительные координаты всех BS сети и записать их, например, в таблицу 5, при этом учитывать, что каждая BS имеет свой уникальный кодовый сдвиг.
Таблица 5 − Координаты размещения BS в сети с DSSS
NBS |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Коорди- |
(0,0) |
(1,-1) |
(0,-1) |
(-1,0) |
(2,0) |
(3,-1) |
(2,-1) |
наты BS |
|
|
|
|
|
|
|
(а, b) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кодовый |
12 |
192 |
3072 |
49150 |
786432 |
125829 |
201326 |
сдвиг |
|
|
|
|
|
12 |
592 |
|
|
|
|
|
|
|
|
В некоторых сетях различение BS и мобильных станций может осуществляться передачей дополнительных сигналов в канале управ-
28
ления или иным способом как в [2], [8] и [12] и поэтому различение BS может осуществляться с помощью других ортогональных кодов и по иному правилу.
Секторизацию сот необходимо провести в зависимости от плотности проживающего населения, трафика и вероятности отказов при необходимости повышения производительности в сети, используя модели Эрланга [6]. Для этого первую ячейку, можно разделить на секторы, количество которых можно взять равным . Территориальную модель проектируемой сети можно построить, используя приведенную выше методику для любых видов множественного доступа.
1.3 Расчет интерференционных помех территориальной модели однородной сети
По территориальной модели сети составленной ранее можно рассчитать расстояния до мешающих станций, которые работают на одних и тех же каналах. Их количество зависит от размерности кластера и определяется как С – 1. Тогда, зная теорему Пифагора для прямоугольного треугольника, можно рассчитать расстояния до ближайших мешающих базовых станций с одинаковыми каналами, используя рисунок 7. Зная длину катетов прямоугольного треугольника, можно определить длину гипотенузы. Длину катетов или гипотенузы необходимо определять с помощью сетки территориальной модели. И с помощью теоремы Пифагора определять расстояние до мешающих станций.
Например, территориальная модель для расчета семиэлементного кластера представлена на рисунке 8. Сведения рисунка 8 можно упростить с учетом того, что самые худшие условия для связи наблюдаются тогда, когда мобильная станция находится в точке А, рисунок 9, т. е. при переходе из одной соты в другую. Расстояние от точки А до точек М1…М6, это расположение BS с одинаковыми каналами для С=7.
29
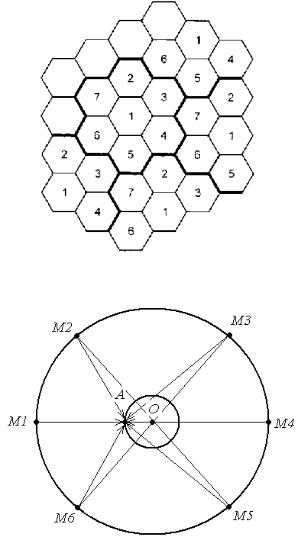
Рисунок 8 – Графическое представление территориальной модели с размерностью кластера С=7
Рисунок 9 – Графическое представление расстояний до мешающих станций
30
