Двойные и дуальные числа

Рассмотрим числа, по форме похожие на комплексные числа.

Определение. Кольцом двойных чисел называется коммутативное кольцо Д₁, содержащее поле действительных чисел R, элемент , такой, что и всякий называются двойными числами, а запись - алгебраической формой записи двойного числа.

Определение. Кольцом дуальных чисел называется коммутативное кольцо Д₀, содержащее поле действительных чисел R, элемент , такой, что и всякий элемент из Д₀ представим в виде , где а и b – действительные числа. Элементы из Д₀ называются дуальными числами, а запись - алгебраической формой записи дуального числа.

Для доказательства существования двойных и дуальных чисел достаточно рассмотреть множество упорядоченных пар действительных чисел (а, b) и определить на нем соответствующим образом сложение и умножение.

Общий взгляд на комплексные, двойные и дуальные числа

Теорема. Следующие утверждения эквивалентны:

1. система есть либо поле комплексных чисел, либо кольцо двойных чисел, либо кольцо дуальных чисел;

2. система есть коммутативное кольцо, которое содержит поле действительных чисел и элемент , такой, что всякий элемент из К представим в виде a+bj, где a,b.

Доказательство. Очевидно, что из 1) следует 2). Докажем, что из 2) следует 1).

Пусть коммутативное кольцо содержит поле и элемент и всякий элемент из К представим в виде a+bj, где a,b. Тогда существуют такие u,v, что. Тогда и . Рассмотрим три возможных случая.

1. <0, тогда = -k², . ; .

Обозначим , тогда ; .

Тогда Следовательно, , где Итак, система - поле комплексных чисел.

2. >0, тогда = m², . ; .

Обозначим , тогда ; .

Если предположить, что , то получим , что противоречит условию. Следовательно, .

Тогда Следовательно, , где Итак, система - кольцо двойных чисел.

3. =0, тогда. .

Обозначим , тогда ; .

Тогда , где

Итак, система - кольцо дуальных чисел.

Лекция 9.

VI. Кватернионы

Определим новую числовую систему, заменяя R на C. Будем искать систему со свойствами:

1) - поле;

2) в поле 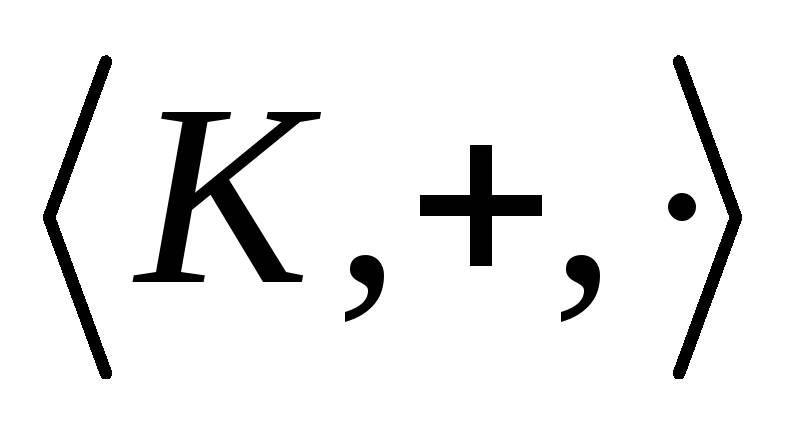содержится поле комплексных чисел , с мнимой единицей i, ();

3) в К существует новая мнимая единица такая, что ;

4) всякий элемент из К представим в виде x+yj, где .

В поле умножение коммутативно, поэтому (i-j)(i+j)=i²+ij-ji+j²=i²-j²=-1-(-1)=0. В поле нет делителей нуля, поэтому j=i или j=-i, что противоречит условию 3.

Таким образом, от требования коммутативности умножения придется отказаться, этот отказ приводит к понятию кольца с делением, или тела.

Определение. Телом называется ненулевое кольцо с единицей, в котором всякий ненулевой элемент обратим.

Будем теперь искать тело со свойствами 2-4.

Умножение в К зависит от правила умножения мнимых единиц i и j. Это правило найдено Гамильтоном в 1843 г.

Определение. Системой кватернионов называется тело , удовлетворяющее следующим условиям:

1. оно содержит поле комплексных чисел 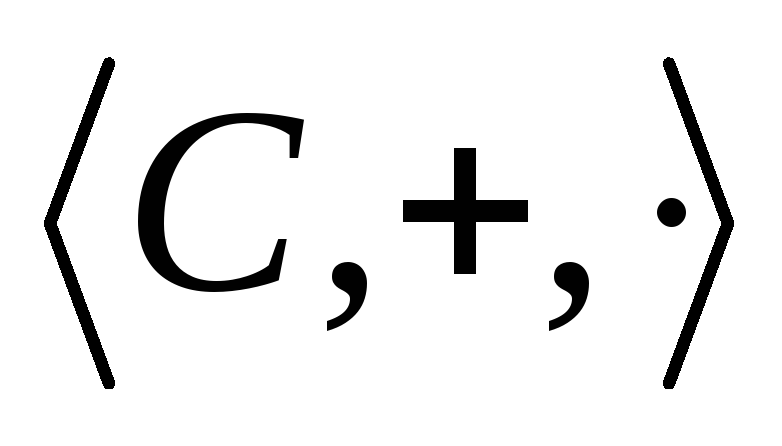с полем действительных чисел и мнимой единицей i, ();

2. оно содержит новую мнимую единицу j, , , причем для мнимой единицы j и любого действительного числа коммутативный закон выполняется (aj=ja);

3. (ij)²=-1;

4. K=C+Cj=.

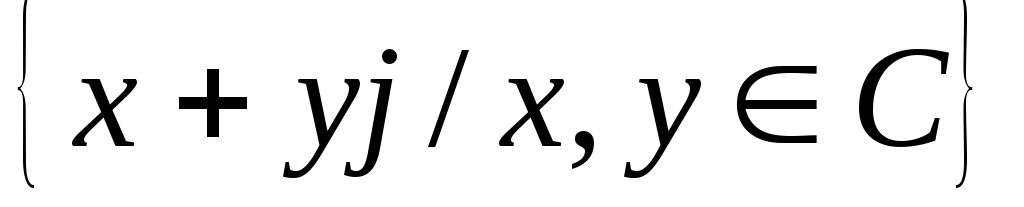Всякий элемент из К называется кватернионом, а система называется телом кватернионов.

Обозначим ij=k, тогда i²=j²=k²=ijk=-1.

Умножение мнимых единиц выполняется по следующему правилу:

×	i	j	k
i	-1	k	-j
j	-k	-1	i
k	j	-i	-1

Если x=a+bi, y=c+di, a,b,c,d, то x+ej=(a+bi)+(c+di)j=a+bi+cj+dk.

Запись a+bi+cj+dk называется алгебраической формой записи кватерниона. Слово «кватернион» означает «четверное» число.

Можно доказать, что множество единиц образуют группу относительно умножения. Она называется группой кватернионов. Сумма и произведение кватернионов определяются как сумма и произведение многочленов.

Для доказательства существования тела кватернионов в качестве модели кватерниона a+bi+cj+dk можно рассматривать упорядоченные четверки действительных чисел (a, b, c, d).

Пары (a, b) и четверки (a, b, c, d) действительных чисел можно рассматривать как векторы пространств R² и R⁴.

Тогда множество действительных чисел можно рассматривать как одномерное векторное пространство над полем R; множество комплексных чисел, а также множества двойных и дуальных чисел, - как двумерные векторные пространства над полем R; множество кватернионов – как четырехмерное пространство над полем R.

Определение. Алгеброй над полем Р называется кольцо 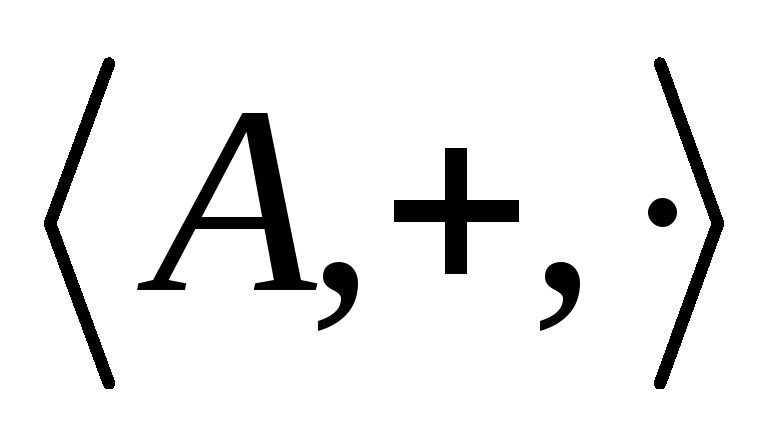, аддитивная группа которого является п-мерным векторным пространством над полем Р, причем

.

Рангом алгебры А над полем Р называется размерность п векторного пространства, rangA=n. Единица е кольца называется единицей алгебры.

Общий взгляд на действительные, комплексные числа и кватернионы

Определение. Алгеброй с делением называется алгебра А над полем Р в случае, когда кольцо является телом.

Теорема Фробениуса. Алгебра А над полем R является алгеброй с делением конечного ранга над полем действительных чисел тогда и только тогда, когда есть либо поле действительных чисел, либо поле комплексных чисел, либо тело кватернионов.

Теорема Фробениуса утверждает, что нельзя придумать «новую числовую систему», которая, так же как и тело кватернионов, была бы, с одной стороны, телом, а с другой стороны – конечным векторным пространством над полем R. Это утверждение придает вид завершенности теории числовых систем.

Однако, если отказаться от ассоциативности умножения, то можно получить бесконечно много не ассоциативных конечномерных алгебр с делением над полем R.

Если в определении тела свойство ассоциативности заменить на свойство альтернативности: (aa)b=a(ab), (ba)a=b(aa), то получим определение альтернативной алгебры с делением над полем.

Обобщенная теорема Фробениуса утверждает, что единственной альтернативной не ассоциативной конечномерной алгеброй с делением над полем R является алгебра октав, придуманная А. Кэли. Она содержит 8 единиц, всякий ее элемент записывается в виде линейной комбинации с действительными коэффициентами и реализуется, как вектор из R⁸.

Выводы:

1. Поле действительных чисел – это единственная алгебра с делением над полем R ранга 1.

2. Поле С – это единственная коммутативная и ассоциативная алгебра с делением над полем R конечномерного ранга r>1.

3. Тело кватернионов – это единственная ассоциативная, но не коммутативная алгебра с делением над полем R конечного ранга.

4. Алгебра октав – это единственная альтернативная , но не ассоциативная алгебра с делением над полем R конечного ранга.

Кватернионы и октавы называются гиперкомплексными числами.

52