
III. Рациональные числа
В кольце целых чисел деление не всегда выполнимо. В связи с этим возникает необходимость расширить кольцо целых чисел до такого множества, в котором операция сложения и умножения обладали такими же свойствами и кроме того операция умножения была бы обратима. Очевидно, что искомое множество есть поле.
Определение. Полем рациональных чисел называется минимальное поле, являющееся расширением кольца целых чисел.
Предположим, что поле Q
– рациональных чисел существует. В этом
поле уравнение bx = a,
где a и b
– любые целые числа,
![]() ,
должно иметь решение.
,
должно иметь решение.
Если a делится на b,
то x – целое число,
если же a не делится
на b, то x
– элемент поля Q, не
являющийся целым числом. Т.к. в любом
поле уравнение bx = a
при
![]() имеет единственное решение, то в поле
Q элемент x
должен определяться парой (a,
b) целых чисел однозначно.
имеет единственное решение, то в поле
Q элемент x
должен определяться парой (a,
b) целых чисел однозначно.
Пусть уравнения bx = a
и dy = c,
где
![]() и
и
![]() имеют
равные решения x = y.
имеют
равные решения x = y.
Пары (a, b) и (c, d) определяют одно и тоже число.
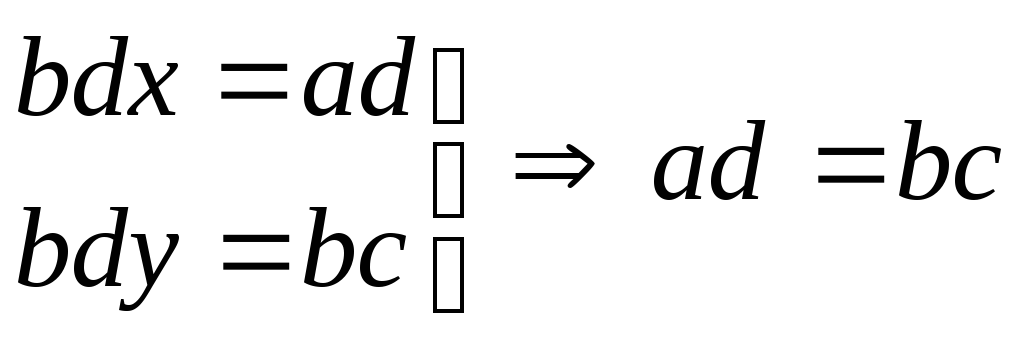 (1)
(1)
Если x и y любые элементы поля Q, то
bd(x + y) = ad + bc, т.е. сумма решений уравнений bx = a и dy = c должны определяться парой целых чисел
(ad + bc,bd) (2)
Найдем произведение элементов x и y
bdxy = ac (ac,bd) (3)
Рассмотрим множество M
всевозможных пар целых чисел. (a,
b) при
![]() , причем две пары (a,
b) и (b,a)
будем считать вообще говоря, различными.
Для удобства каждую пару (a,
b) целых чисел будем
обозначать через
, причем две пары (a,
b) и (b,a)
будем считать вообще говоря, различными.
Для удобства каждую пару (a,
b) целых чисел будем
обозначать через
![]() ,
т.е. (a, b)
=
,
т.е. (a, b)
=
![]() .
Будем называть эту пару дробью.
.
Будем называть эту пару дробью.
Определение. Две дроби
![]() и
и
![]() называются эквивалентными тогда, и
только тогда, когда ad
= bc.
называются эквивалентными тогда, и
только тогда, когда ad
= bc.
![]() ~
~
![]() ad
= bc
ad
= bc
Следствие. Отношение эквивалентности дробей рефлексивно, симметрично и транзитивно.
-
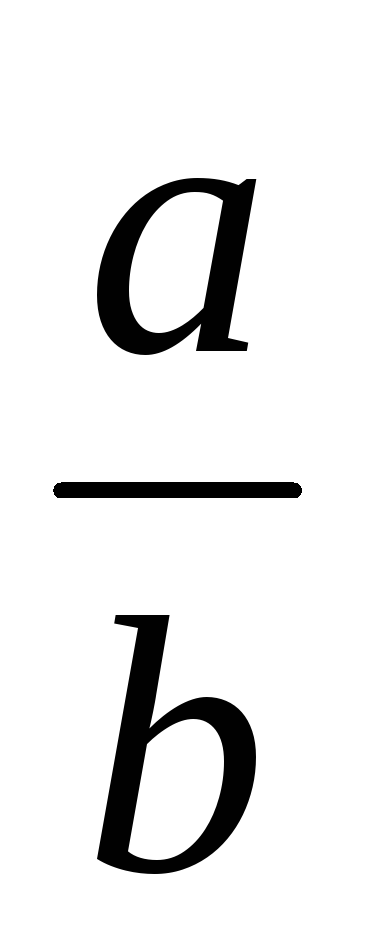 ~
~
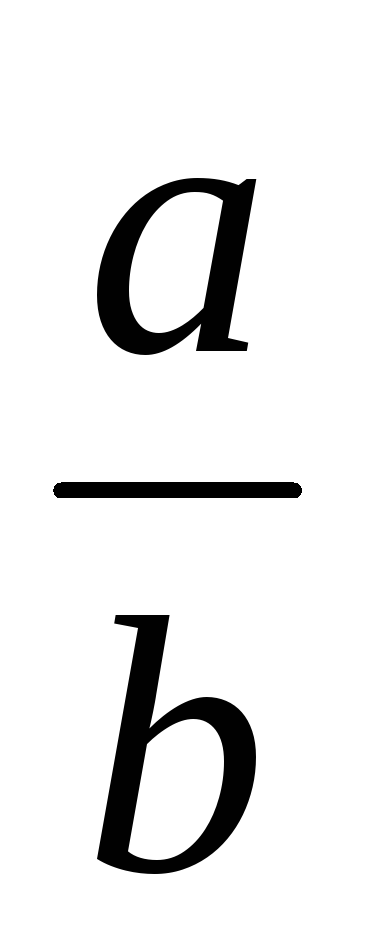
-
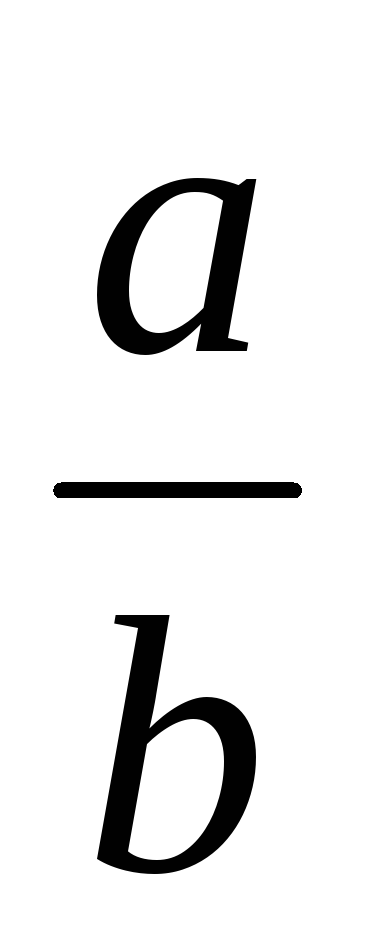 ~
~
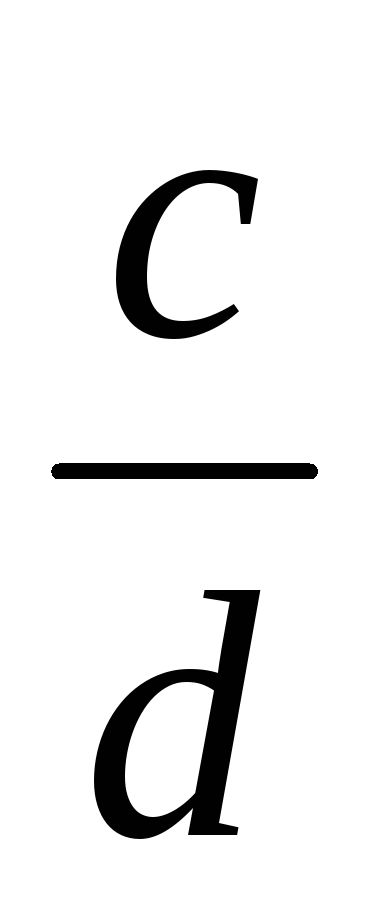 =>
=>
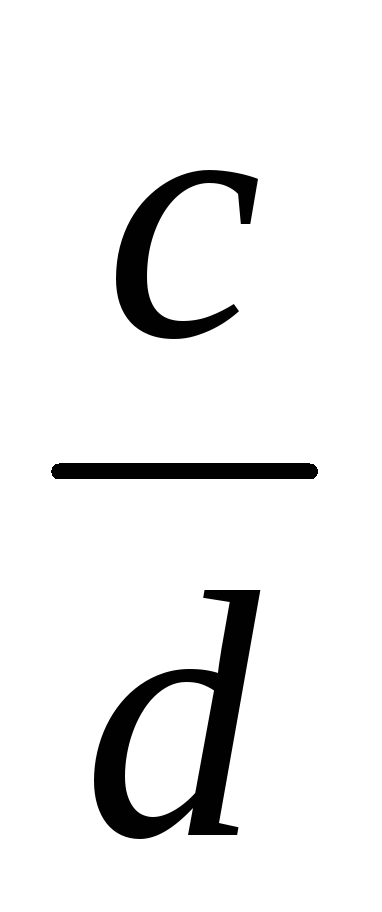 ~
~
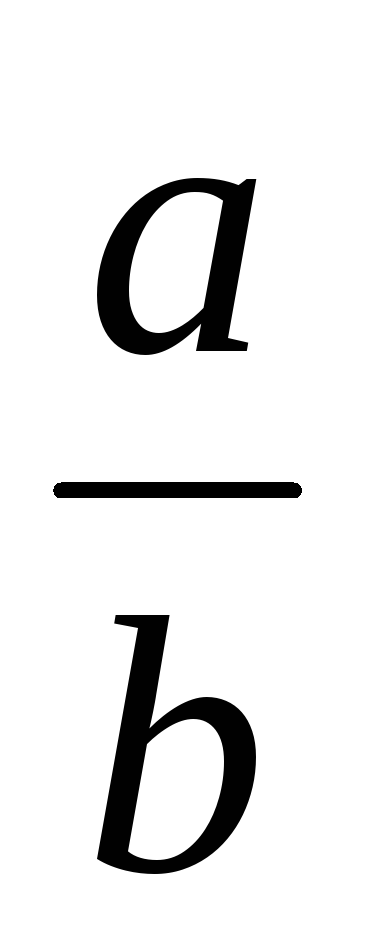
-
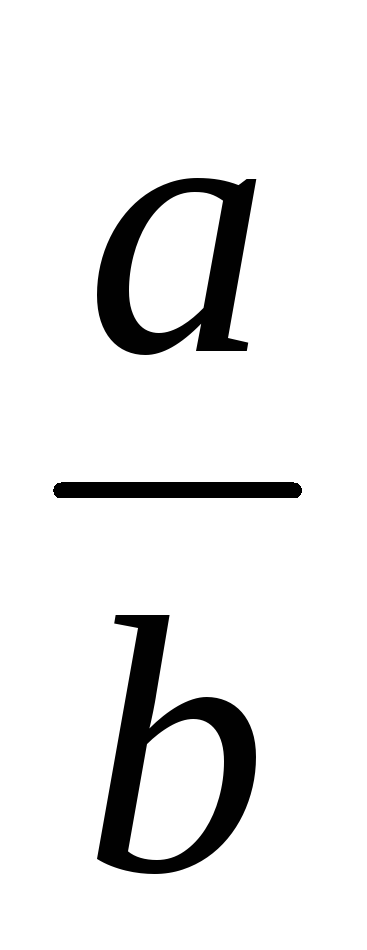 ~
~
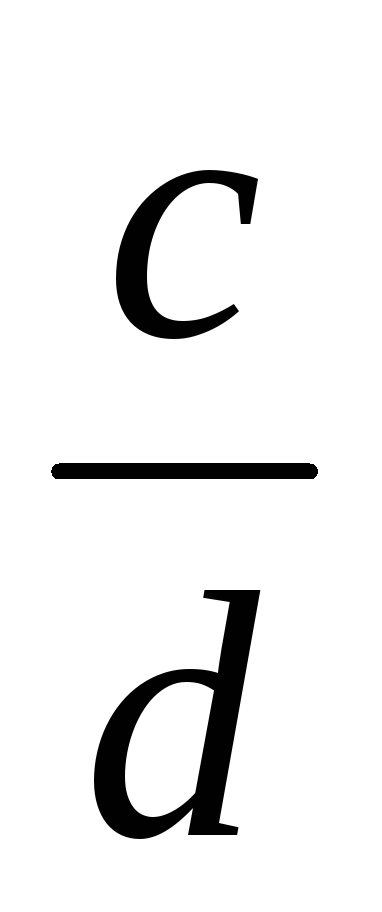

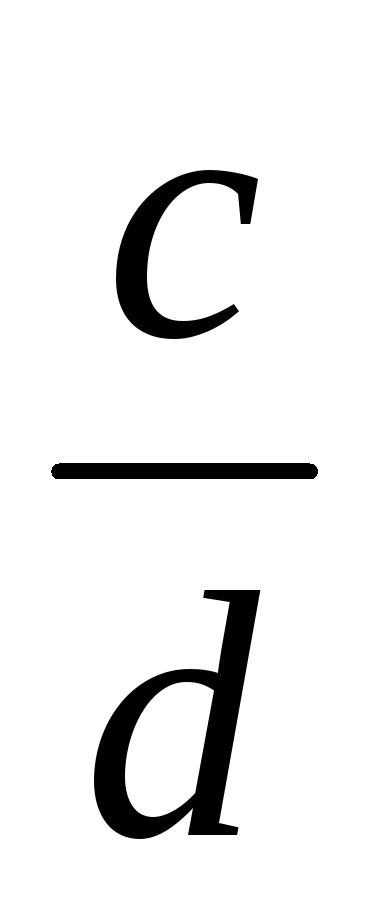 ~
~
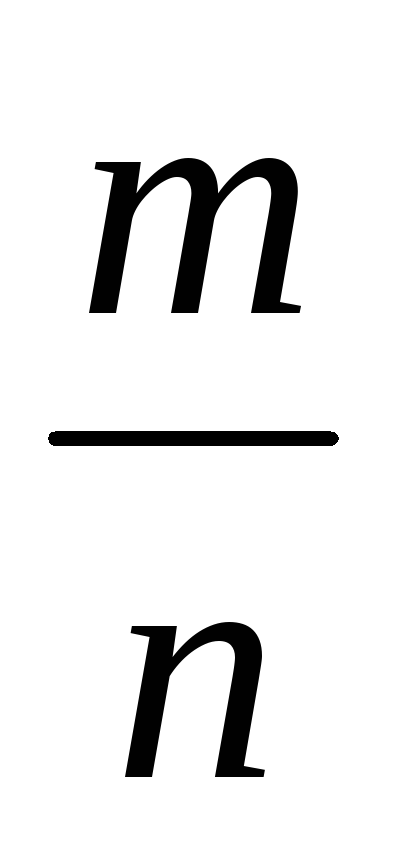 =>
=>
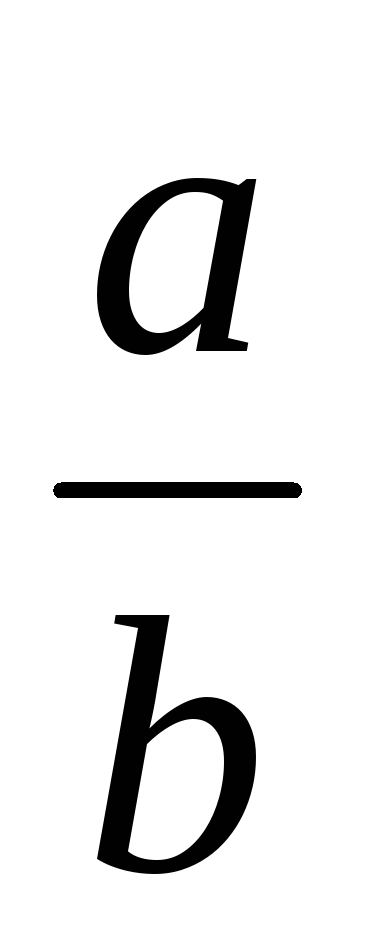 ~
~
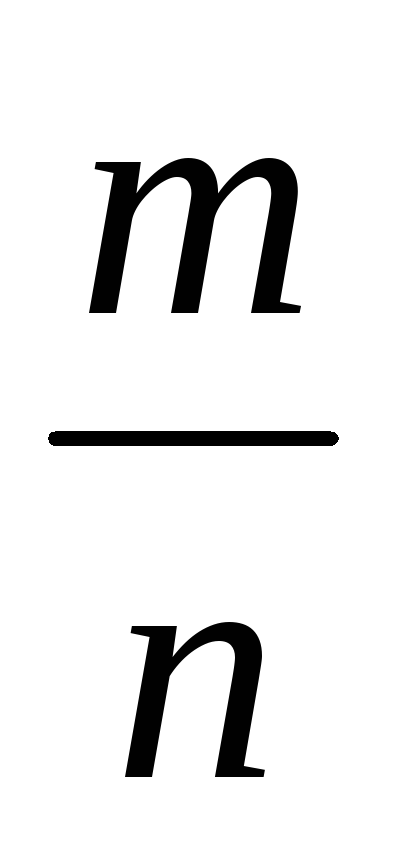
Проверим выполнение свойства 3.
ad = bc и cn = dm
and = bcn
![]() bcn = bdm
=> and
= bdm =>
an = bm
=>
bcn = bdm
=> and
= bdm =>
an = bm
=>
![]() ~
~
![]()
Следствие. Если оба компонента дроби
![]() умножить на одно и тоже целое число
умножить на одно и тоже целое число
![]() ,
то получим дробь
,
то получим дробь
![]() эквивалентную дроби
эквивалентную дроби
![]() .
.
Доказательство.
abk = abk
=>
![]() ~
~
![]()
Определение. Суммой двух дробей
![]() и
и
![]() называется дробь
называется дробь
![]() ,
т.е.
,
т.е.
![]() +
+
![]() =
=
![]()
Следствие. Если в сумме
![]() +
+![]() заменить слагаемые дробями, им
эквивалентными, то результат будет
эквивалентен первоначальному результату.
заменить слагаемые дробями, им
эквивалентными, то результат будет
эквивалентен первоначальному результату.
Доказательство.
![]() ~
~
![]() и
и
![]() ~
~
![]()
ab’ = b’a => ab’dd’ = a’bdd’ почленно сложим
cd’ = dc’ => cd’bb’ = dc’bb’
ab’dd’
+ cd’bb’
= a’bdd’
+ dc’bb’
=>
![]() ~
~
![]()
Определение. Произведением двух
дробей
![]() и
и
![]() называется дробь
называется дробь
![]() ,
т.е.
,
т.е.
![]() ∙
∙![]() =
=
![]()
Следствие. При замене обеих сомножителей дробями, эквивалентными этим сомножителям, получается результат, эквивалентный первоначальному результату.
Доказательство.
![]()
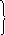 ~
~
![]()
![]() ~
~
![]() => acd’b’
= a’bc’d
, т.е.
=> acd’b’
= a’bc’d
, т.е.
![]() ~
~
![]()
Отношение эквивалентности полностью
определяет разбиение множества M
всех дробей
![]() на классы попарно эквивалентных
элементов. Класс, которому принадлежит
дробь
на классы попарно эквивалентных
элементов. Класс, которому принадлежит
дробь
![]() ,
будем обозначать через
,
будем обозначать через
![]()
Рассмотрим множество всех таких классов
![]() .
.
![]() =
=
![]()
![]() ~
~
![]()
Этим полностью определяется отношение
равенства для элементов
![]()
Определение. Суммой двух классов
из
![]() называется тот класс, которому принадлежит
сумма каких-нибудь представителей
слагаемых
называется тот класс, которому принадлежит
сумма каких-нибудь представителей
слагаемых
Определение. Произведением двух
классов из
![]() называется тот класс, которому принадлежат
произведение каких-нибудь представителей
перемножаемых классов.
называется тот класс, которому принадлежат
произведение каких-нибудь представителей
перемножаемых классов.
Следствие. Во множестве
![]() выполняются все аксиомы поля.
выполняются все аксиомы поля.
1.
![]() +
+
![]() =
=
![]() =
=
![]() =
=
![]() +
+
![]() =>
=>
![]() +
+
![]() =
=
![]() +
+
![]()
2.
![]() +
+
![]() +
+
![]() =
=
![]() =
=
![]() +
+
![]() +
+
![]() =>
=>
![]() +
+
![]() +
+
![]() =
=
![]() +
+
![]() +
+
![]()
3. Найдем решение уравнения
![]() +
+
![]() =
=
![]()
Предположим, что уравнение
![]() +
+
![]() =
=
![]() имеет решение
имеет решение
![]() ,
которое подставлено в уравнение, тогда
,
которое подставлено в уравнение, тогда
![]() =
=
![]() => bcy
+ bdx =
ady
=> bcy
+ bdx =
ady
bdx
= (ad -
bc)y
=>
![]() =
=
![]()
![]() +
+
![]() =
=
![]() =
=
![]() ~
~
![]()
![]() ~
~
![]()
Решением уравнения
![]() +
+
![]() =
=
![]() будет класс
будет класс
![]() =
=
![]() -
-
![]()
-
Нулем в этом множестве является класс
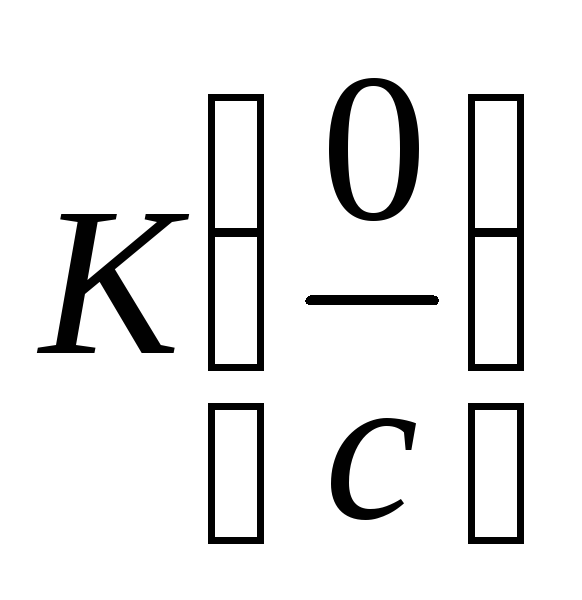 ,
где
,
где
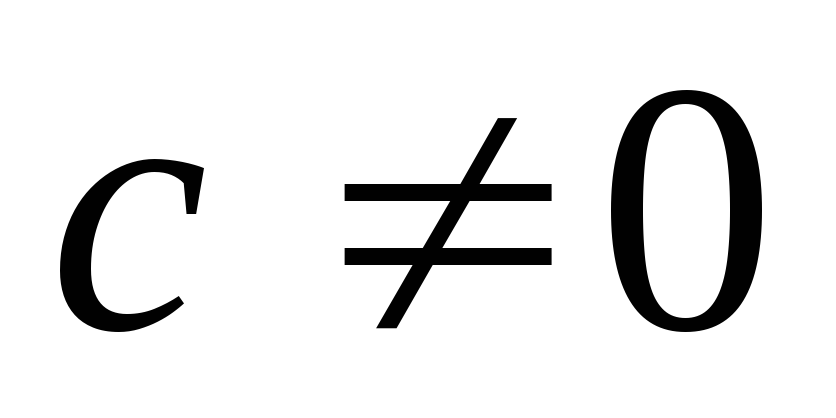 ,
т.к.
,
т.к.
![]() +
+
![]() =
=
![]() ~
~
![]()
-
Элементом, противоположным классу
 ,
будет класс
,
будет класс
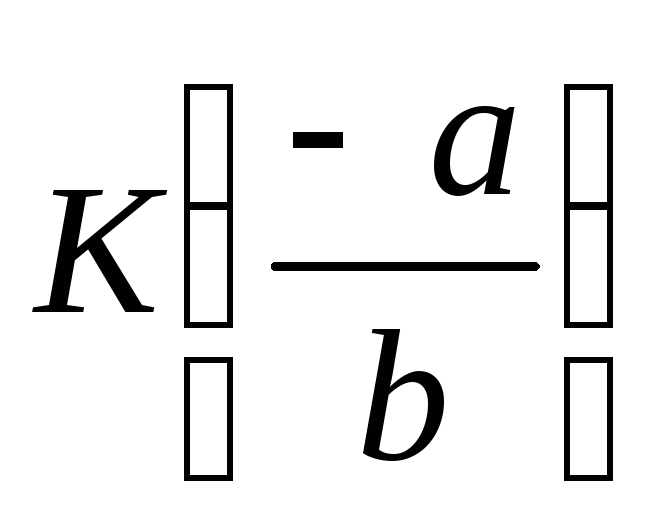 ,
т.к.
,
т.к.
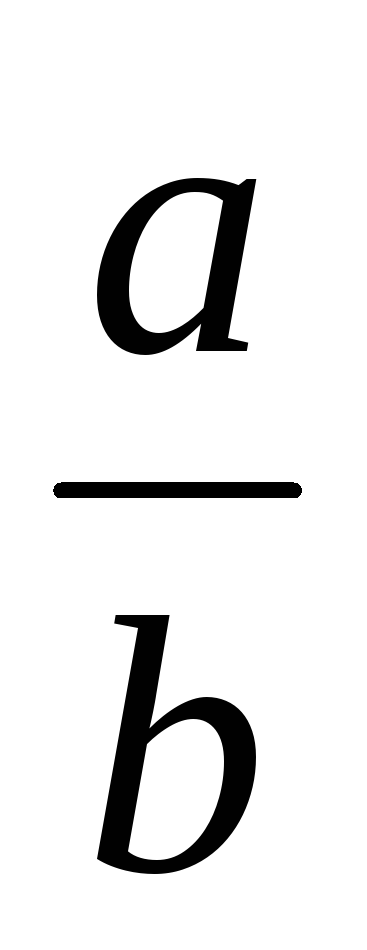 +
+
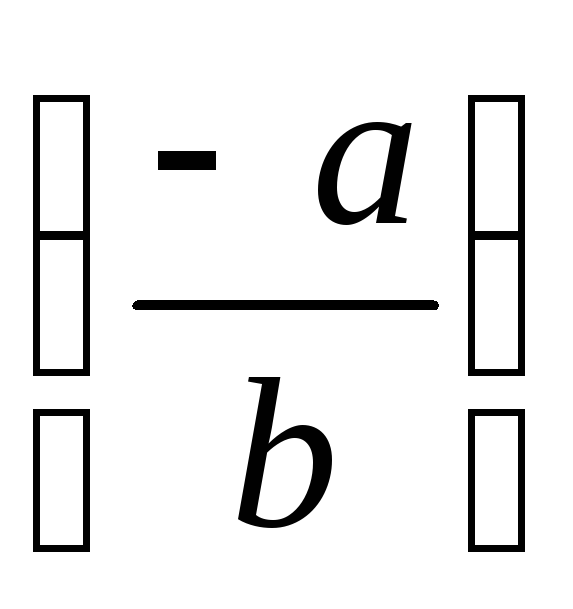 =
=
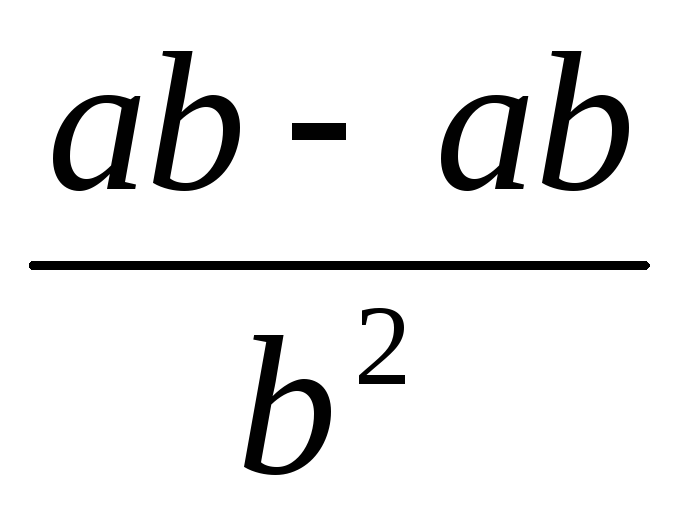 =
=
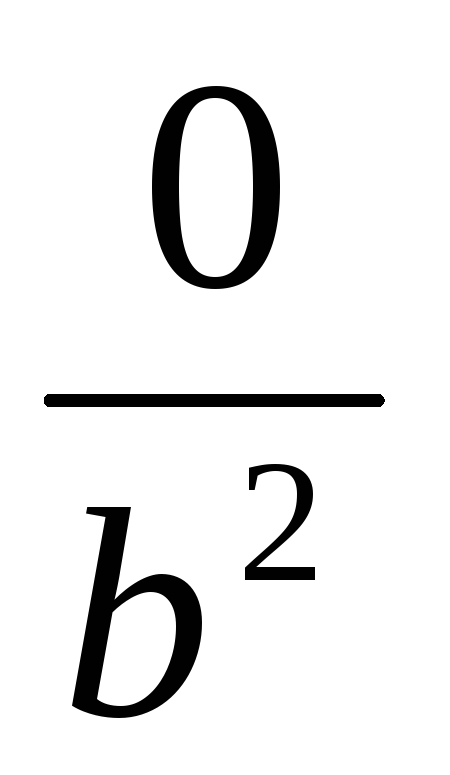 ~
~
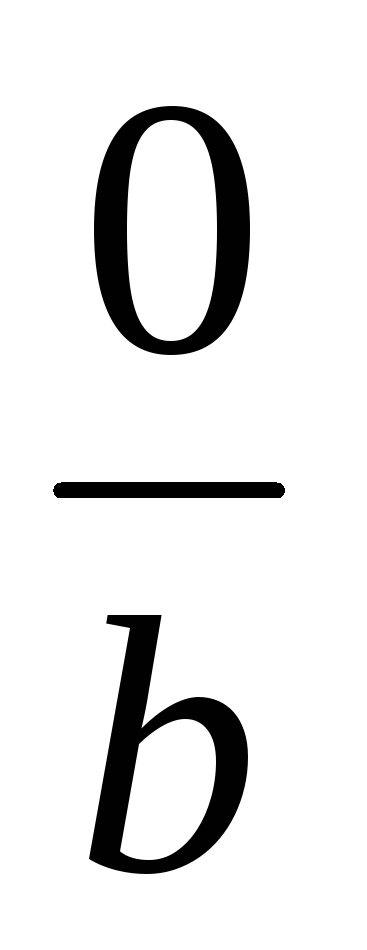
4.
![]() ∙
∙![]() =
=
![]() ∙
∙![]() =>
=>
![]()
![]() =
=
![]()
![]()
5.
![]() ∙
∙![]() ∙
∙![]() =
=
![]() ∙
∙![]() ∙
∙![]() =>
=>
![]()
![]()
![]() =
=
![]()
![]()
![]()
6.
![]() ∙
∙![]() +
+
![]() =
=
![]() ∙
∙![]() +
+
![]() ∙
∙![]() =>
=>
![]()
![]() +
+
![]() =
=
![]()
![]() +
+
![]()
![]()
7. Уравнение
![]()
![]() =
=
![]() при
при
![]() всегда имеет решение во множестве
всегда имеет решение во множестве
![]() .
.
Решением будет класс
![]() это следует из
это следует из
![]() ∙
∙![]() =
=
![]() ~
~
![]()
Сравнение классов попарно эквивалентных дробей и действия с неравенствами.
Определение. Назовем дробь
![]() положительной (
положительной (![]() > 0), если ab > 0; нулевой
(
> 0), если ab > 0; нулевой
(![]() = 0), если ab = 0; отрицательной
(
= 0), если ab = 0; отрицательной
(![]() < 0), если ab < 0.
< 0), если ab < 0.
Т.к. кольцо Z целых
чисел расположено, то для дробей
![]() имеет место одно, и только одно, из
соотношений:
имеет место одно, и только одно, из
соотношений: ![]() > 0
> 0
![]()
![]() = 0
= 0
![]()
![]() < 0
< 0
Определение. Класс
![]() называется положительным классом, если
все его представители положительны;
нулевым классом, если все представители
нулевые дроби; отрицательным, если все
его представители отрицательны.
называется положительным классом, если
все его представители положительны;
нулевым классом, если все представители
нулевые дроби; отрицательным, если все
его представители отрицательны.
Теорема. Для любого класса
![]() имеет место одно, и только одно, из
свойств:
имеет место одно, и только одно, из
свойств:
![]() - положителен,
- положителен,
![]() - нулевой класс,
- нулевой класс,
![]() - отрицателен.
- отрицателен.
Доказательство.
Пусть![]() и
и
![]() ~
~
![]() => ad ~ bc
=> (ab)(cd)
= b2c2
= (bc)2 > 0 (
=> ad ~ bc
=> (ab)(cd)
= b2c2
= (bc)2 > 0 (![]() ,
т.к. тогда было бы c =
d = 0, что следует из
равенства ad = bc).
Если ab > 0, то cd
> 0, если ab < 0, то cb
< 0. Следовательно, если в классе
,
т.к. тогда было бы c =
d = 0, что следует из
равенства ad = bc).
Если ab > 0, то cd
> 0, если ab < 0, то cb
< 0. Следовательно, если в классе
![]() содержится положительная дробь, то и
все представители этого класса
положительны; если в
содержится положительная дробь, то и
все представители этого класса
положительны; если в
![]() содержится отрицательная дробь, то и
все представители этого класса
отрицательны; все нулевые дроби и только
они, содержатся в одном и том же классе.
содержится отрицательная дробь, то и
все представители этого класса
отрицательны; все нулевые дроби и только
они, содержатся в одном и том же классе.
Теорема. Сумма и произведение
положительных классов из
![]() положительны.
положительны.
Доказательство.
Пусть
![]() и
и
![]() - положительные классы, т.е. ab
>0 и cd > 0.
- положительные классы, т.е. ab
>0 и cd > 0.
Покажем, что
![]() +
+
![]() =
=
![]() > 0 и
> 0 и
![]()
![]() =
=
![]() > 0.
> 0.
Из ab > 0
![]() cd > 0 => abd2
> 0
cd > 0 => abd2
> 0
![]() b2cd
> 0
b2cd
> 0
![]() (ad + bc)bd
= abd2 + b2cd
> 0
(ad + bc)bd
= abd2 + b2cd
> 0
![]()
![]() (ac)(bd)
= (ab)(cd)
> 0
(ac)(bd)
= (ab)(cd)
> 0
Из последних неравенств следует справедливость утверждения.
Если определить
![]() >
>
![]() тогда, и только тогда, когда разность
тогда, и только тогда, когда разность
![]() -
-
![]() =
=
![]()
положительна, то в поле
![]() будут выполнены все аксиомы расположения,
т.е. поле
будут выполнены все аксиомы расположения,
т.е. поле
![]() будет расположенным полем.
будет расположенным полем.
Построение поля рациональных чисел.
Рассмотрим множество всех классов из
![]() ,
в которых содержится дробь вида
,
в которых содержится дробь вида
![]() ,
где a
,
где a![]() .
Обозначим это множество
.
Обозначим это множество
![]() .
Два класса
.
Два класса
![]() =
=
![]() a
= b, т.к.
a
= b, т.к.
![]() ~
~
![]() a
= b.
a
= b.
Этим установлено взаимнооднозначное
соответствие между элементами множества
![]() и всеми числами кольца Z.
Это соответствие будет изоморфным
относительно сложения, умножения и
отношения “больше”, установленных в
этих множествах, т.к. из
и всеми числами кольца Z.
Это соответствие будет изоморфным
относительно сложения, умножения и
отношения “больше”, установленных в
этих множествах, т.к. из
![]() +
+
![]() =
=
![]() ,
, ![]()
![]() =
=
![]() ,
,
![]() >
>
![]()
всегда следуют верные соотношения a
+ b = c,
ab = d,
a > b
и обратно. Следовательно существует
поле Q, содержащее в
себе в качестве подкольца (каждое поле
есть подкольцо) кольцо целых чисел Z,
причем
![]() .
.
Искомое поле Q строим следующим образом:
Каждый класс вида
![]() заменяем целым числом a,
а все остальные элементы поля
заменяем целым числом a,
а все остальные элементы поля
![]() оставляем на месте. Правила сложения,
умножения и сравнения по величине для
чисел полученного поля Q
вытекают из соответствующих правил
в поле
оставляем на месте. Правила сложения,
умножения и сравнения по величине для
чисел полученного поля Q
вытекают из соответствующих правил
в поле
![]() .
.
Элементы поля Q называют рациональными числами, а целые числа, рассматриваемые как элементы поля Q, называются целыми рациональными числами.
Отождествим в каждом классе все дроби,
т.е. будем считать любые эквивалентные
дроби
![]() ~
~
![]() лишь различными обозначениями одного
и того же рационального числа. При таком
соглашении любая дробь класса
лишь различными обозначениями одного
и того же рационального числа. При таком
соглашении любая дробь класса
![]() будет обозначать целое число a.
будет обозначать целое число a.
Получим обычное обозначение рациональных
чисел в виде дробей
![]() ,
где a – числитель,
b – знаменатель
дроби.
,
где a – числитель,
b – знаменатель
дроби.
Определение. Две дроби
![]() и
и
![]() называются равными тогда, и только
тогда, когда ad = bc.
называются равными тогда, и только
тогда, когда ad = bc.
![]() =
=
![]() Это следствие дает возможность приведения
дробей к общему знаменателю и сокращения
дробей.
Это следствие дает возможность приведения
дробей к общему знаменателю и сокращения
дробей.
Сложение и умножение дробей производится по правилу
![]() +
+
![]() =
=
![]() ;
; ![]() ∙
∙![]() =
=
![]()
Правило вычитания:
![]() -
-
![]() =
=
![]()
При сравнении дробей по величине будем всегда считать знаменатели этих дробей положительными числами
![]() -
-
![]() =
=
![]() =>
=>
![]() >
>
![]() ad
> bc
ad
> bc
![]()
![]() <
<
![]() ad
< bc
ad
< bc
Минимальность поля Q
следует из того, что любое поле, являющееся
расширением кольца целых чисел Z,
должно содержать все дроби
![]() ,
т.е. должно содержать в себе поле Q
в качестве подполя, т.к. это поле обязано
содержать решения всех уравнений вида
bx = a
с целыми коэффициентами, где
,
т.е. должно содержать в себе поле Q
в качестве подполя, т.к. это поле обязано
содержать решения всех уравнений вида
bx = a
с целыми коэффициентами, где
![]() .
.
Теорема. Поле рациональных чисел Q архимедовски расположено, т.е. в поле Q выполняется аксиома Архимеда.
Доказательство.
![]() и
и
![]() - произвольные рациональные числа, где
- произвольные рациональные числа, где
![]() > 0.
> 0.
-
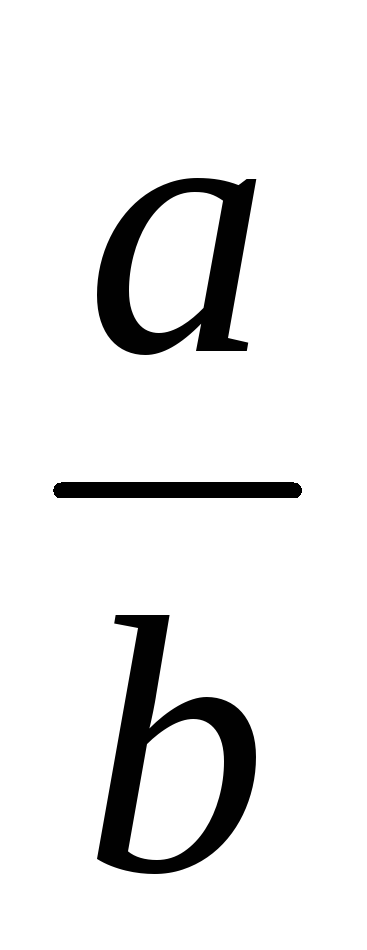 <
<
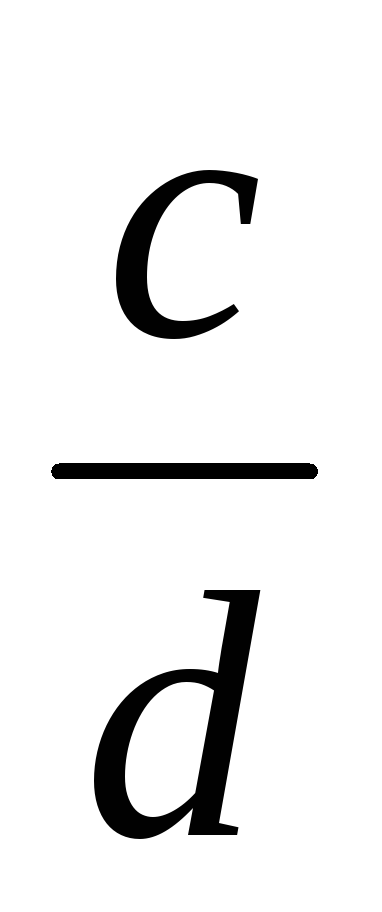 ,
то достаточно взять n
= 1, т.к.
,
то достаточно взять n
= 1, т.к.
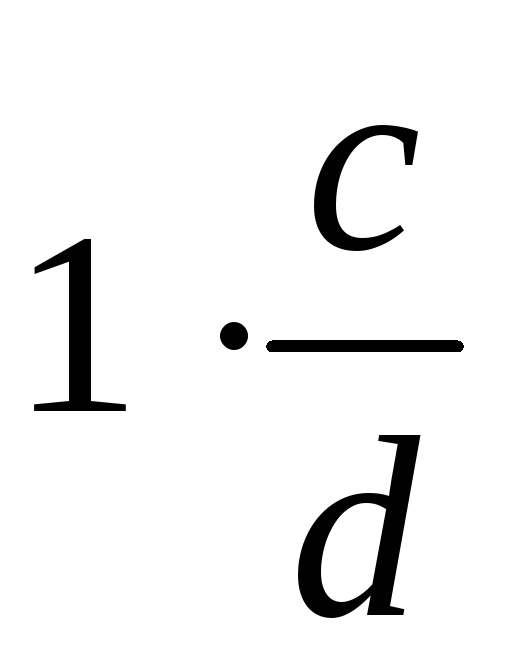 >
>
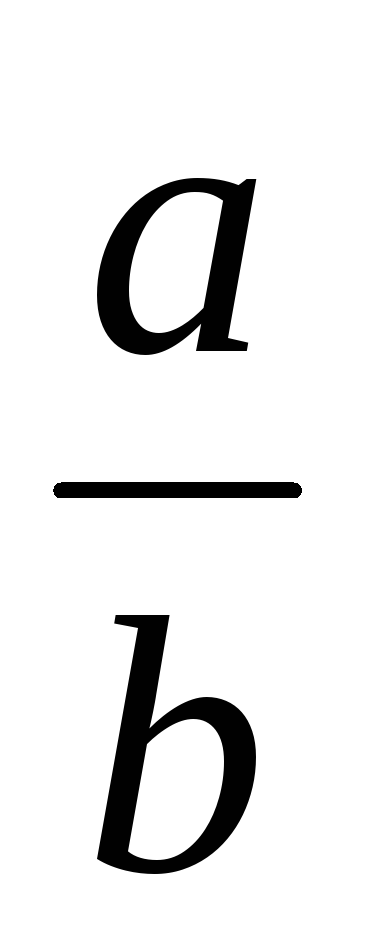
-
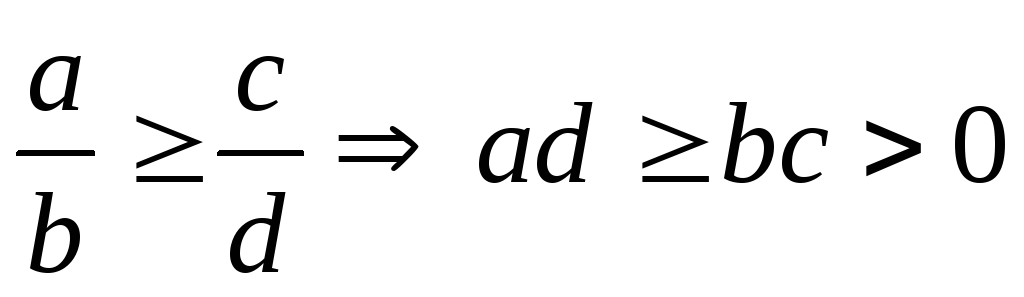 ,
для целых чисел аксиома Архимеда
выполняется.
,
для целых чисел аксиома Архимеда
выполняется.
nbc > ad
=> n![]() =
=
![]() >
>
![]()
Теорема. Поле рациональных чисел Q обладает свойством плотности, т.е. между двумя произвольными различными рациональными числами заключено по меньшей мере одно рациональное число.
Доказательство.
Пусть
![]() >
>
![]() ,
где b > 0 и d
> 0;
,
где b > 0 и d
> 0;
![]()
Тогда
![]() будет одним из чисел, удовлетворяющее
условиям
будет одним из чисел, удовлетворяющее
условиям
![]() >
>
![]() >
>
![]() ,
т.к.
,
т.к.
ad > bc
и
![]() -
-
![]() =
=
![]() =
=
![]() > 0 =>
> 0 =>
![]() >
>
![]()
![]() -
-
![]() =
=
![]() =
=
![]() > 0 =>
> 0 =>
![]() >
>
![]()
Кольцо целых чисел этим свойством не обладает.
Лекция 7.
