
- •Мнимые и комплексные числа. Действие над комплексными числами в алгебраической формуле.
- •Типы уравнений
- •Алгебраические уравнения
- •Квадратные уравнения. Формулы нахождения корней. Сколько корней имеет уравнение в зависимости от дискриминанта. Неполные квадратные уравнения.
- •Дискриминант
- •Неполные квадратные уравнения
- •Теорема Виета. Разношение квадрата трехчлена на линейные множители.
- •Система двух линейных уравнений с двумя неизвестными. 4 способа решений Системы двух линейных уравнений с двумя неизвестными
- •Графический способ решения линейных систем. Случай единственного решения, множества решений и не имеет решения в зависимости от коэффициента.
- •Решение систем двух, трех линейных уравнений с двумя, тремя неизвестными по правилу Крамера. Способом определителей.
- •Квадратные неравенства (решение: графически и методом промежутков).
- •Отбор корней квадратного трехчлена по условиям и расположение нулей квадратичной функции на числовой прямой.
- •Функции. Свойства функций.
- •Обратные функции. Свойства взаимообратных функций. Примеры обратных функций.
- •Свойство и графики где:
- •14. Показательная функция. Свойство и график.
- •15. Понятие о логарифме числа. Свойство логарифмов. Логарифмические тождества. Понятие логарифма
- •16. Логарифмическая функция. Свойства и график.
- •17. Основные способы решения логарифмических уравнений и логарифмических неравенств.
- •Логарифмические неравенства
- •18. Единичная числовая окружность. Определение тригонометрических функций числового аргумента. Область определения и значений.
- •19. Вычисления числовых значений тригонометрических функций для аргументов
- •20. Знаки тригонометрических функций. Свойство четности и нечетности.
- •21. Основные тригонометрические тождества. Выражение тригонометрических функций через другие функции.
- •22. Периодичность тригонометрических функций.
-
Решение систем двух, трех линейных уравнений с двумя, тремя неизвестными по правилу Крамера. Способом определителей.
Системы трёх линейных уравнений с тремя неизвестными имеют вид:
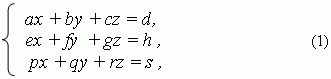
где a, b, c, d, e, f, g, h, p, q, r, s – заданные числа; x, y, z – неизвестные. Числа a, b, c, e, f, g, p, q, r – коэффициенты при неизвестных; d, h, s – свободные члены. Решение этой системы может быть найдено теми же двумя основными методами, рассмотренными выше: подстановки исложения или вычитания. Мы же рассмотрим здесь подробно только метод Крамера.
Во-первых, введём понятие определителя третьего порядка. Выражение
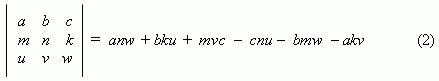
называется определителем третьего порядка.
Запоминать это выражение не нужно, так как его легко получить, если переписать таблицу (2), добавив справа первые два столбца. Тогда оно вычисляется путём перемножения чисел, расположенных на диагоналях, идущих от a, b, c – направо ( со знаком « + » ) и от c, a, b – налево ( со знаком « – » ), и затем суммированием этих произведений:
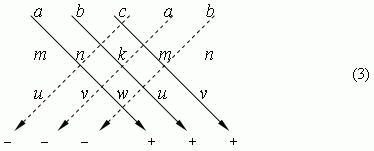
Используя определитель третьего порядка (2), можно получить решение системы уравнений (1) в виде:
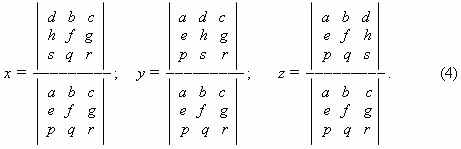
Эти формулы и есть правило Крамера для решения системы трёх линейных уравнений с тремя неизвестными.
-
неравенство. Основное свойство неравенства. Решение линейных неравенств. Решение систем двойного неравенства. Неравенства с модулем..
Два выражения (числовые
или буквенные), соединённые одним из
знаков: «больше»
(>), «меньше» (<), «больше или
равно» (![]() «меньше
или равно» (
«меньше
или равно» (![]() образуют неравенство (числовое
или буквенное). Любое справедливое
неравенство называется тождественным.
Например, тождественны следующие
неравенства: 3 · 7
– 20 > 2 · 4 10, a² 0, | 5
| > 3. (Почему?). В зависимости от знака
неравенства мы имеем либо строгие
неравенства (
> ,
< ) , либо нестрогие (
образуют неравенство (числовое
или буквенное). Любое справедливое
неравенство называется тождественным.
Например, тождественны следующие
неравенства: 3 · 7
– 20 > 2 · 4 10, a² 0, | 5
| > 3. (Почему?). В зависимости от знака
неравенства мы имеем либо строгие
неравенства (
> ,
< ) , либо нестрогие ( ![]()
![]() Запись 5a
Запись 5a ![]() b означает,
что 5a либо
меньше 4b, либо
равно ему. Буквенные величины, входящие
в неравенство, могут быть как известными,
так и неизвестными. Решить
неравенство – значит найти границы,
внутри которых должны находиться
неизвестные, так чтобы неравенство было
справедливым. Решить
систему неравенств – значит найти
границы, внутри которых должны находиться
неизвестные, так чтобы все неравенства,
входящие в
систему, были справедливы одновременно.
b означает,
что 5a либо
меньше 4b, либо
равно ему. Буквенные величины, входящие
в неравенство, могут быть как известными,
так и неизвестными. Решить
неравенство – значит найти границы,
внутри которых должны находиться
неизвестные, так чтобы неравенство было
справедливым. Решить
систему неравенств – значит найти
границы, внутри которых должны находиться
неизвестные, так чтобы все неравенства,
входящие в
систему, были справедливы одновременно.
Основные свойства неравенств.
|
1. |
Если a < b, то b > a ; или если a > b, то b < a . |
|
2. |
Если a > b, то a + c > b + c; или если a < b, то a + c < b + c. То есть, можно прибавлять (вычитать) одно и то же число к обеим частям неравенства. |
|
3. |
Если a > b и c > d, то a + c > b + d . То есть, неравенства одного смысла (с одинаковым знаком > или < ) можно почленно складывать. Заметим, что неравенства одного смысла нельзя почленно вычитать одно из другого, так как результат может быть неверным. |
|
4. |
Если a > b и c < d, то a – c > b – d . Или если a < b и c > d, то a – c < b – d . То есть,неравенства противоположного смысла можно почленно вычитать одно из другого, и брать знак неравенства, являющегося уменьшаемым. |
|
5. |
Если a > b и m > 0, то ma > mb и a/m > b/m . То есть, обе части неравенства можно умножить или разделить на одно и то же положительное число. Неравенство при этом сохраняет свой знак. |
|
6. |
Если a > b и m < 0, то ma < mb и a/m < b/m . То есть, обе части неравенства можно умножить или разделить на одно и то же отрицательное число. Неравенство при этом меняет свой знак на обратный.
|
Некоторые важные неравенства.
1.
| a
+ b | ![]() a b
| . Модуль
суммы меньше или равен сумме модулей.
a b
| . Модуль
суммы меньше или равен сумме модулей.
2. a
+ 1
/ a ![]() 2 a
– положительно
). Равенство будет только при a =
1.
2 a
– положительно
). Равенство будет только при a =
1.
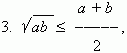 ( a и b – положительны
). Равенство только при a = b.
( a и b – положительны
). Равенство только при a = b.
Среднее геометрическое не больше среднего арифметического.
В общем случае это неравенство имеет вид:
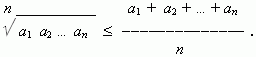
Числа a1 , a2 , …, an - положительны. Равенство имеет место, если только все числа равны.
